Физические теории 8 страница

W=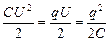 (7.8.1)

Подобным образом, рассматривая процесс зарядки уединенного проводника, получим для его энергии формулы:

W=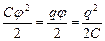 (7.8.2)

Заряд проводника складывается из суммы точечных зарядов на его поверхности: q= S q_i. Все эти заряды находятся в точках поля с одинаковыми потенциалами j _i =j. Получаем, что энергия системы точечных зарядов равна:

W=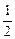 S q_ij_I (7.8.3)

Здесь q_i. - точечный заряд с номером i, j_i – потенциал поля, созданного всеми остальными зарядами системы в точке, где находится заряд q_i.

2. Заряды создают в пространстве электрическое поле. Можно считать, что энергия сосредоточена в объеме поля с объемной плотностью w=W/V, где V- объем электрического поля. Выразим объемную плотность энергии электрического поля w_Е через его силовую характеристику – напряженность Е. Для этого рассмотрим однородное поле, в нем энергия равномерно распределена по объему. Таким является поле плоского конденсатора. Учитывая, что в плоском конденсаторе E=s /e₀e, s=q/S, U=Ed, С=e₀eS/d, V=Sd, получаем:

w_E=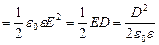 (7.8.4)

Формула (7.8.4) применима не только к однородному, но и к любому электростатическому полю. Если поле Е=Е (x,y,z) известно в каждой точке, то интегрированием можно найти энергию в любой части его объема: W=.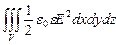

Глава 8. Постоянный электрический ток.

§ 8.1. Электрический ток: сила тока, плотность тока

1. Электрическим током называется упорядоченное движение электрических зарядов, сопровождающееся переносом заряда через некоторую поверхность S, например, через поперечное сечение проводника. Мы уже видели, что движущиеся под действием электрического поля заряды являются посредниками, превращающими его энергию в механическую работу. Электрический ток может производить такое действие в макроскопических масштабах, а также приводить к выделению тепла, возникновению магнитного поля, некоторых химических, оптических и других явлений. Энергия движущихся зарядов передается по проводам на большие расстояния, а также легко преобразуется в другие виды энергии. Электрический ток широко используется в технике, он является важнейшим энергетическим фактором экономики государства.

Для поддержания электрического тока нужны свободные заряды и электрическое поле. Длительное время токи в проводниках могут существовать только при определенных условиях. Заряды, участвующие в создании тока, называют носителями тока. В металлах такими носителями являются свободные электроны, в электролитах - положительные и отрицательные ионы. Носителями тока могут быть макроскопические частицы – пылинки и капельки, несущие на себе избыточный электрический заряд (капельки дождя во время грозы). Носители очень малы, и непосредственно наблюдать их движение практически невозможно.

Ток проявляет себя следующими действиями: магнитным, тепловым, химическим. Ток создает вокруг себя магнитное поле, это его универсальное свойство, проявляющееся при движении любых заряженных частиц. Тепловое действие тока используется в электронагревательных приборах. Химическое действие тока наблюдается в электролитах и применяется, например, в гальванической технике для нанесения тончайших металлических слоев на поверхность изделия.

Носители участвуют в тепловом движении. Средняя скорость их хаотического движения определяется той же формулой, что для молекул газа в тепловом равновесии. Тепловое движение не создает электрического тока, из-за его хаотичности потоки носителей сквозь любую мысленно выделенную поверхность в проводнике за любой промежуток времени одинаковы в обоих направлениях, так что переносимый ими суммарный заряд равен нулю.

При появлении электрического поля на носители тока начинает действовать сила, и к их хаотическому движению добавляется направленное движение. При столкновениях носители теряют направленную скорость, и вновь начнут ее приобретать на следующем отрезке свободного пробега. В результате положительные носители тока перемещаются в направлении поля, а отрицательные – против поля. Это движение называется дрейфом, а его средняя скорость называется скоростью дрейфа. Подобную картину можно наблюдать в рое мошек или комаров при ветре. Именно дрейф создает направленный перенос электрического заряда, т.е. электрический ток.

2. Количественной характеристикой тока является сила тока – i. Пусть через поверхность площадью S за промежуток времени dt ток переносит заряд dq, тогда сила тока через эту поверхность

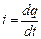(8.1.1)

Единицей силы тока в СИ является ампер (А): 1А = 1Кл / 1с. Сила тока – алгебраическая величина. За направление тока принято направление упорядоченного движения положительных зарядов, отрицательные носители движутся против тока.

Постоянным называется ток, сила и направление которого не изменяются со временем. Силу постоянного тока обозначают I.

I=q/t (8.1.2)

Здесь q – заряд, переносимый током за время t через рассматриваемую поверхность.

Еще одна характеристика – вектор плотности тока 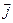, направленный вдоль вектора скорости упорядоченного движения положительных носителей и численно равный силе тока через поверхность единичной площади:

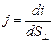(8.1.3)

Здесь di – сила тока через элементарную площадку, расположенную в данной точке перпендикулярно направлению дрейфа носителей, площадью dS _^.

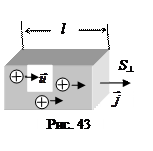В проводнике с током выделим часть его в виде прямоугольного параллелепипеда объемом V= S _^ l (рис.43). Положительные носители движутся со скоростью дрейфа 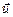перпендикулярно к боковой поверхности S _^. Обозначим заряд носителя тока q ₀, концентрацию носителей n, тогда суммарный заряд носителей в выделенном объеме составит q= q ₀ nV= q ₀ n S _^ l. За время t=l/u этот заряд будет перенесен через S _^, так что сила тока составит I=q/t= q ₀ nu S _^. Соответственно плотность тока j=q₀nu. Вектор плотности тока 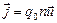показан на рис. 43. Ток в металлических проводниках создают свободные электроны. Обозначая их заряд е, получаем:

j=enu (8.1.4)

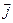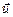Здесь n – концентрация свободных электронов, u – их скорость дрейфа. Заметим, что заряд электрона отрицательный, и векторы скорости дрейфа и плотности тока направлены противоположно, так что в формуле (8.1.4) можно поставить знаки векторов над и . Поле вектора плотности тока, подобно другим векторным полям[29], рисуют линиями, касательные к которым указывают его направление, а густота линий – его модуль. Они называются линиями тока. Линии тока есть траектории упорядоченного движения носителей.

§ 8.2. Механизм электропроводности

1. Линии постоянного тока замкнутые. Это значит, что цепь постоянного тока должна быть замкнутой. Под действием электростатического поля положительные заряды перемещаются от большего потенциала к меньшему, а отрицательные в противоположном направлении. Такой участок цепи называется однородным. Достигнув конца такого участка, носители снова должны попасть к его началу. Следовательно, в замкнутой цепи обязательно должен быть участок, на котором положительные носители движутся от меньшего потенциала к большему, а отрицательные по-прежнему навстречу им. На таком участке помимо сил электростатического поля на носители должны действовать другие силы, преодолевающие действие электрических сил. Такие силы называются сторонними, они имеют неэлектростатическую природу. Участок цепи, где действуют сторонние силы, называется неоднородным, и им является источник тока. Таким образом, постоянный ток в замкнутой цепи создает источник постоянного тока. Он характеризуется электродвижущей силой e и внутренним сопротивлением r [30].

2. Применим знакомый нам из молекулярной физики статистический метод для рассмотрения механизма электропроводности, например, в металлическом проводнике. На однородном участке цепи на носитель тока (электрон проводимости) действует только электрическое поле силой F=eE и сообщает ему ускорение a= eE/m. При столкновениях с кристаллической решеткой, причиной которых является тепловое движение, скорость упорядоченного движения носителя падает до нуля. За время свободного пробега t до следующего столкновения она вырастает от нуля до at= eEt/m. Скорость дрейфа (средняя скорость направленного движения), создающая электрический ток, u= at/ 2. Расчеты показывают[31], что средняя скорость теплового движения u >> u, так что t=l/u (l - средняя длина свободного пробега носителя). Используя формулу (8.1.4), получаем: j=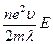. Сомножитель перед Е в правой части формулы не зависит от электрического поля. Он определяется только свойствами проводника: концентрацией носителей тока - n, их массой – m и зарядом - e, скоростью теплового движения - u, длиной свободного пробега - l и называется удельной электропроводностью g материала проводника. В справочных таблицах чаще указывают удельное сопротивление материала r= 1 /g. Поученная нами формула выражает закон Ома для однородного участка цепи в дифференциальной (локальной) форме:

j=gЕ=Е /r (8.2.1)

Работа электрического поля на длине свободного пробега разгоняет носитель до скорости at= eEl/ (mu) и сообщает ему дополнительную кинетическую энергию упорядоченного движения mu ²/2= (eEl)² / (2 mu ²). Теперь при столкновении с частицами материала (его кристаллической решеткой) носители передают им и эту добавочную энергию, которая преобразуется в энергию хаотического движения всех частиц, т.е. во внутреннюю энергию. Такой способ изменения внутренней энергии тела называется передачей ему количества тепла. За единицу времени каждый носитель испытывает 1/ t=u /l столкновений, и столько же раз отдает тепло. Количество тепла, переданное решетке всеми носителями тока в единице объема за единицу времени называется удельным тепловыделением

Q _уд.= n (eEl)² / (2 mu ² t) = 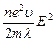. Таким образом, мы получили закон Ленца – Джоуля в дифференциальной (локальной) форме:

Q _уд =gЕ ² =Е ² /r = jЕ (8.2.2)

3. На неоднородном участке цепи (внутри источника тока) на носители кроме кулоновских сил действуют еще сторонние силы. Будем их рассматривать как поле сторонних сил с напряженностью 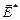и учтем его действие на носители. Тогда закон Ома в дифференциальной форме для неоднородного участка примет вид:

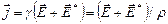(8.2.3)

§ 8.3. Законы постоянного тока.

1. Пусть однородный участок цепи представляет собой однородный проводник длиной l с постоянной по длине площадью поперечного сечения S. Применим формулу (8.2.1), умножив ее левую часть на S, а правую на S l/ l: j S=Е l (S /r l). Учитывая, что jS=I, Е l=j₁ -j ₂ =U, r l / S =R – сопротивление проводника, получаем хорошо знакомый из школы закон Ома для однородного участка цепи:

I= (8.3.1)

2. Протеканию тока по проводнику (упорядоченному движению носителей) мешает тепловое движение. Это проявляется в индивидуальной характеристике проводника – его сопротивлении. Сопротивление проводника зависит от его геометрии и от электропроводности материала. Для однородного проводника постоянного сечения

R=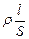 (8.3.2)

Эта формула имеет прозрачный физический смысл: чем длиннее проводник, тем труднее носителям преодолеть этот путь, и, наоборот, чем больше сечение проводника, тем легче им это сделать (полная аналогия с водопроводной трубой). Опыт показывает, что при температурах, не слишком близких к 0 К, удельное сопротивление r линейно растет с ростом температуры. Это свойство используется в термометрах сопротивления – устройствах, измеряющих температуру по электрическому сопротивлению. Рассмотренная нами в предыдущем параграфе модель электронного газа проводимости объясняет эту тенденцию: при увеличении температуры увеличивается средняя энергия хаотического движения, соответственно, учащаются столкновения частиц, мешая направленному движению носителей. Правда, эта классическая модель не дает количественного согласия с теорией, она слишком груба для описания поведения электронов, они не являются макротелами. Некоторые проводящие ток материалы при низких температурах (порядка нескольких кельвин) переходят в сверхпроводящее состояние: сопротивление становится равным нулю. Впервые такое явление было обнаружено у ртути при Т= 4 К в 1911 г. В настоявшее время известно много таких материалов и с более высокой температурой сверхпроводящего состояния. Сверхпроводники представляют большой интерес для техники: для поддержания в них тока не нужен постоянно действующий источник тока. Однако получение сверхпроводящего состояния требует больших энергетических (соответственно, материальных) затрат для охлаждения до сверхнизких температур.

Элементы электрической цепи, обладающие сопротивлением, называются резисторами. На практике для получения необходимого сопротивления используют последовательное и параллельное соединение резисторов друг с другом. При последовательном соединении резисторов их сопротивления складываются:

R= S R_i (8.3.3)

При параллельном соединении резисторов складываются обратные величины сопротивлений (электропроводности):

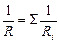(8.3.4)

Выведите формулы (8.3.3) и (8.3.4) самостоятельно.

3. Рассмотрим неоднородный участок цепи постоянного тока, содержащий источник тока, внутри которого на носители действуют электростатическое поле и поле сторонних сил. Для такого участка справедлива формула (8.2.3). Умножим ее скалярно на элемент длины линии тока 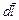и проинтегрируем вдоль линии тока на рассматриваемом участке длиной l. Векторы 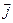и 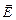, рассматриваемые в этой формуле, направлены по касательной к линии тока, как и 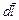, так что в их скалярном произведении можно опустить знаки векторов: 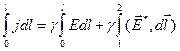. Здесь пределы интегрирования соответствуют начальной – 1 и конечной – 2 точкам линии тока. При j= const ; ;

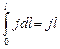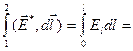e ₁₂ (8.3.5)

e ₁₂ - называется ЭДС (электродвижущая сила), действующая на участке цепи 1-2. Она, как и разность потенциалов, измеряется в вольтах и имеет смысл работы сторонних сил по перемещению единичного положительного заряда по данному участку. ЭДС – скалярная энергетическая характеристика источника тока. Учитывая, что I=jS, R=rl/S=l/gS, получаем формулу закона Ома для неоднородного участка цепи:

IR= j ₁- j ₂+ e ₁₂ (8.3.6)

4. Ранее мы отмечали, что постоянный ток течет в замкнутой электрической цепи, имеющей источник постоянного тока. Внутри источника тока на носители действуют сторонние силы, их работа обеспечивает ток в цепи. Источник тока называют внутренним участком замкнутой цепи. Работа сторонних сил по перемещению положительного единичного заряда по замкнутой цепи называется ЭДС источника тока - e. Направленному движению носителей внутри источника мешает тепловое движение, т.е. источник имеет внутреннее сопротивление – r. e и r – индивидуальные характеристики источника тока, не зависящие от силы тока в нем. Внешний по отношению к источнику тока участок цепи называется нагрузкой. Обычно он состоит из соединенных друг с другом резисторов с общим сопротивлением R. Применим формулу (8.3.6) к замкнутой цепи, в которой точки 1 и 2 совпадают, так что j ₁= j ₂, а общее сопротивление складывается из сопротивлений внешнего и внутреннего участков цепи. В результате получим закон Ома для замкнутой цепи. Его формула:

I=e / (R+r) (8.3.7)

§ 8.4. Работа и мощность тока

Рассматривая механизм электропроводности металлов, мы получили формулу (8.2.2). Применим ее к однородному проводнику длиной l и площадью сечения S. Вычислим количество тепла, выделяемое в этом проводнике током I за время t: Q=Q _уд Vt=jЕlSt=UIt. Мы получили хорошо известную из школьного курса физики формулу закона Джоуля-Ленца. Источником тепла является работа тока. В рассматриваемом нами случае проводник неподвижен, в нем не происходит химических превращений, так что работа тока целиком идет на увеличение внутренней энергии проводника.

Используя закон Ома для однородного участка цепи, приведем разные формулы работы постоянного тока:

A=IUt=I ² Rt =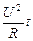 (8.4.1)

Учитывал, что мощность равна работе в единицу времени, получили формулы мощности постоянного тока:

P=IU=I ² R =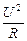 (8.4.2)

Глава 9. Магнитное поле тока

§ 9.1 Магнитное взаимодействие. Магнитное поле

1. Опыт показывает[32], что два параллельных проводника притягиваются, если токи в них текут в одном направлении, и отталкиваются, если токи текут в противоположные стороны (рис.44). Эти же проводники без токов никак не реагируют друг на друга.

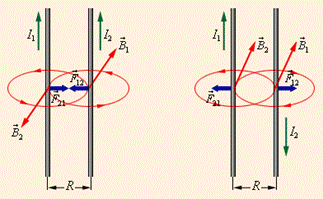Рис. 44

Проводник является электрически нейтральным телом, отрицательный заряд электронных оболочек атомов компенсирует положительный заряд их ядер. Ток в нем создается упорядоченным движением носителей внутри проводника, при этом суммарный электрический заряд проводника по-прежнему равен нулю. Отмеченное взаимодействие проводников с током нельзя объяснить кулоновскими силами.

Еще один опыт – проводник с током оказывает ориентирующее действие на магнитную стрелку. Вблизи прямолинейного тока магнитная стрелка устанавливается поперек проводника, при изменении направления тока на противоположное, стрелка поворачивается на 180⁰. Впервые на это явление обратил внимание Эрстед (1820 г.), именно этот его опыт продемонстрировал связь электричества и магнетизма и явился началом построения теории электромагнитных явлений.

2. Между движущимися электрическими зарядами (токами) возникает дополнительное взаимодействие. Оно называется магнитным и осуществляется магнитным полем. Движущийся электрический заряд изменяет свойства окружающего его пространства, создавая вокруг себя не только электрическое, но и магнитное поле. В отличие от электростатического поля магнитное поле действует только на движущиеся в нем «чужие» электрические заряды. Магнитное поле обнаруживает себя также действием на проводники с током и постоянные магниты[33]. Силовая характеристика магнитного поля называется магнитной индукцией 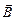. В СИ магнитную индукцию измеряют в тесла (Тл). Магнитное поле известно, если известен вектор 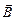в каждой его точке. Как и электрическое поле, магнитное поле можно изображать силовыми линиями. В магнитном поле это линии магнитной индукции: С помощью железных опилок (миниатюрных магнитных стрелок) силовые линии магнитного поля можно визуализировать. Направление вектора магнитной индукции в данной точке указывает касательная к силовой линии, густота силовых линий вблизи этой точки равна (пропорциональна) модулю магнитной индукции.

Помимо 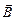есть еще одна связанная с ним дополнительная характеристика: напряженность магнитного поля 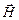. В СИ напряженность магнитного поля измеряют в амперах на метр (А/м). В вакууме 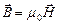, m ₀ – магнитная постоянная, в СИ m ₀=4p^.10⁷Гн/м. В веществе 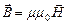, где m - магнитная проницаемость вещества, безразмерная величина.

§ 9.2. Закон Био-Савара-Лапласа

1. Этот закон позволяет рассчитать магнитное поле, созданное тонким произвольной формы проводником с током. Лаплас теоретически обобщил результаты экспериментального изучения Био и Саваром магнитного поля вокруг проводников с током (1820 г.). На рис.45 представлен отрезок криволинейного проводника, направление тока в нем указано стрелкой. Выделим элемент длины проводника dl. Элементом тока называется вектор 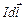, он направлен по касательной к проводнику в данной точке. Элементарное магнитное поле, созданное этим элементом тока в некоторой точке пространства (ее положение относительно элемента тока задает вектор 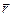), выражает закон Био-Савара-Лапласа:

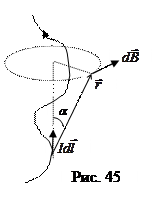
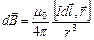(9.2.1)

Вектор 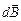направлен перпендикулярно векторам 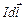и 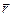по правилу векторного произведения, т.е.по касательной к изображенной на рис. 45 окружности. Его модуль

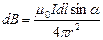(9.2.2)

Магнитное поле, созданное всеми элементами тока проводника, найдем по принципу суперпозиции:

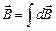(9.2.3)

Рассмотрим примеры расчета магнитного поля тока.

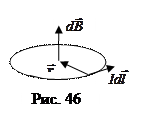2. Поле в центре кругового тока (рис.46). По тонкому проводнику, имеющему форму окружности радиуса r, течет постоянный ток I. Векторы 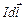и 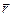взаимно перпендикулярны, первый направлен по касательной к окружности, второй – по радиусу в центр. Векторы 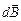всех элементов тока направлены вдоль оси окружности, так что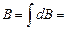 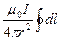. Кружок на интеграле означает, что перемещение образует замкнутый контур, его длина 2p r. Магнитная индукция в центре кругового витка с током

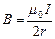(9.2.4)

Отметим, что направление вектора магнитной индукции в центре кругового 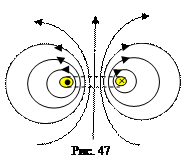тока и направление тока в витке связаны правилом правого винта.

Подобным образом можно рассчитать магнитное поле в любой точке. На рис. 47 показано сечение витка плоскостью, в которой лежит его ось. Желтые кружки обозначают сечение проводника с током, крестик и точка указывают направление тока в нем. Магнитное поле изображено силовыми линиями, стрелками указано их направление. Обратите внимание, что силовые линии магнитного поля всегда замкнуты. Силовая линия, совпадающая с осью витка, замыкается на бесконечности, остальные за пределами границ рисунка.

3. Поле прямолинейного тока (рис. 48). Вектор 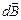перпендикулярен плоскости прямоугольного треугольника, гипотенуза которого равна r, и катет 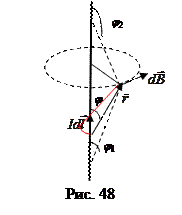b=rsinj противолежит углу j. 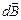направлен по касательной к окружности радиуса b с центром на проводнике с током. Его величина 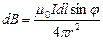. Найдем магнитное поле, которое в указанной на рисунке точке создает отрезок проводника, заданный углами j ₁ и j ₂. Выразим dl и r через j. При перемещении по проводнику на dl получается новый треугольник (его гипотенуза нарисована красной линией), угол увеличится на dj. Новое положение гипотенузы получается поворотом отрезка r на такой центральный угол. Учитывая малость dj, получаем, что проекция на проводник дуги окружности r dj равна dl= rdj / sinj. Заметим, что все элементы прямолинейного тока создают в этой точке одинаково направленные векторы магнитной индукции, так что

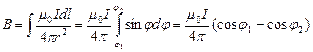(9.2.5)

Для бесконечно длинного проводника j ₁=0, j ₂=p, так что

(9.2.6)

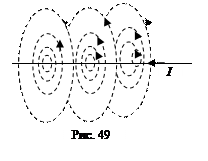Заметим, что силовые линии магнитного поля прямолинейного тока являются концентрическими окружностями, их плоскости перпендикулярны проводнику с током, а центры лежат на проводнике. На рис. 49 показан отрезок бесконечно длинного прямолинейного проводника с током, лежащего в плоскости рисунка. Его силовые линии – концентрические окружности – в плоскости рисунка изображены овалами. Правые половинки овалов соответствуют частям окружностей перед плоскостью рисунка, левые - за плоскостью рисунка. Направление силовых линий связано с направлением тока в проводнике правилом правого винта. Густота силовых линий уменьшается при удалении от проводника

9.3. Вихревой характер магнитного поля.

1. Математически поле векторов характеризует поток через поверхность и циркуляция вектора по контуру. Электростатическое поле создается неподвижными электрическими зарядами и является потенциальным. Математически это выражается формулами (7.3.1) и (7.4.9). Первая из них – теорема Гаусса - констатирует, что положительные заряды служат «истоками» силовых линий, отрицательные – их «стоками», так что поток через замкнутую поверхность определяют заряды, находящиеся внутри нее. Вторая формула констатирует, что циркуляция вектора напряженности электростатического поля по контуру равна нулю, так как кулоновские силы консервативные, и их работа на замкнутом пути равна нулю.

Дата добавления: 2014-01-06