Общее уравнение плоскости

Теорема 2. В общей декартовой системе координат плоскость выражается уравнением первой степени

.

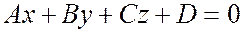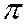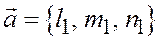Доказательство. Фиксируем на плоскости произвольную точку и возьмем два неколлинеарных вектора и 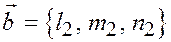, каждый из которых компланарен плоскости . Тогда на основании предыдущей теоремы уравнение плоскости можно записать в виде

или

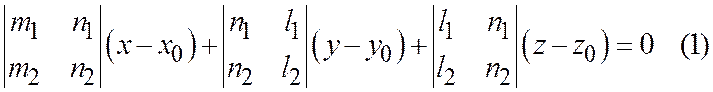
Так как векторы и 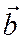неколлинеарны, то по крайней мере один из определителей

не равен нулю (§ 36, теорема 5), следовательно уравнение (1) первой степени относительно x, y, z. Если еще положить

;

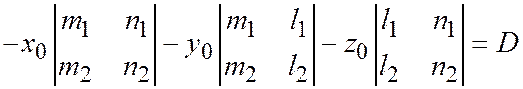то уравнение (1) примет вид

.

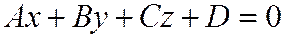Уравнение называется общим уравнением плоскости.

Теорема 3 (обратная). Всякое уравнение первой степени

(2)

в общей декартовой системе координат является уравнением плоскости.

Доказательство. Пусть - какое-нибудь решение данного уравнения, то

(3)

Данное уравнение (2) будет эквивалентно уравнению, которое мы получим, отняв почленно из уравнения (2) равенство (3)

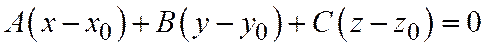. (4)

Одно из чисел А, В, С не равно 0; пусть, например, , тогда уравнение (4) эквивалентно уравнению

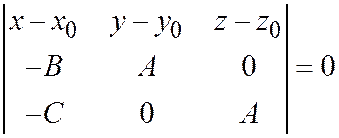. (5)

В самом деле, последнее уравнение после раскрытия определителя примет вид

,

или (т.к. )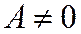

.

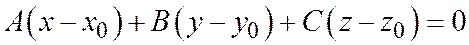Далее, векторы

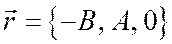и

неколлинеарны, поскольку один из определителей

не равен нулю (в силу условия 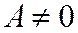не равен нулю первый определитель). Поэтому уравнение (5), а значит и данное уравнение (2), определяет (на основании теоремы 1) плоскость, проходящую через точку 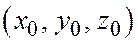компланарно двум неколлинеарным векторам (в случае ):

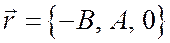и .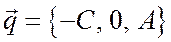

Аналогично доказывается, что данная плоскость (в случае ) компланарна векторам и , между собой неколлинеарным, а в случае - векторам

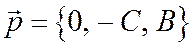и ,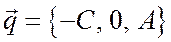

которые также неколлинеарны. ЧТД.

В декартовой прямоугольной системе координат вектор перпендикулярен плоскости, заданной уравнением 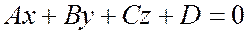. В самом деле, возьмем на плоскости, заданной общим уравнением 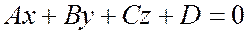относительно декартовой прямоугольной системы координат, две произвольные различные точки 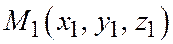и , тогда

,

откуда

или

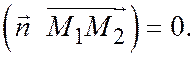
Значит вектор перпендикулярен любой прямой 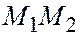, лежащей на данной плоскости, значит, перпендикулярен самой плоскости.

В общей декартовой системе координат вектор может и не быть перпендикулярным плоскости, заданной уравнением ; этот вектор называется главным вектором плоскости, заданной уравнением 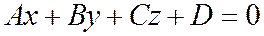относительно общей декартовой системе координат.

Дата добавления: 2014-01-07