
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Бесконечные производные
|
|
|
|
Введем в рассмотрение понятие бесконечной производной. Пусть функция 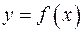 определена в некоторой окрестности
определена в некоторой окрестности 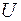 точки
точки 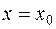 и непрерывна в самой точке
и непрерывна в самой точке 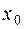 .
.
Если
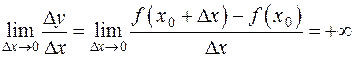 ,
,
то будем говорить, что функция имеет в точке 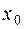 производную, равную
производную, равную  , и будем писать
, и будем писать
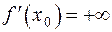 . (4)
. (4)
В этом случае 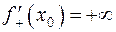 и
и 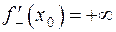 .
.
Если
 ,
,
то будем говорить, что функция имеет в точке 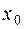 производную, равную
производную, равную 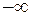 , и будем писать
, и будем писать
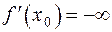 . (5)
. (5)
В этом случае 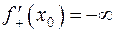 и
и 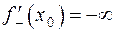 .
.
Если
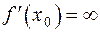 ,
,
но не выполняется, ни одно из условий (4) или (5), то будем говорить, что производная 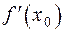 не является бесконечностью определенного знака. Например, эта ситуация имеет место, если
не является бесконечностью определенного знака. Например, эта ситуация имеет место, если
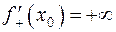 и
и 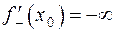
или
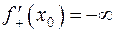 и
и 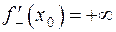 .
.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 843; Нарушение авторских прав?; Мы поможем в написании вашей работы!