Частные производные и частные дифференциалы первого порядка

(4).

Или

Функция f (х, у) называется непрерывной в области, если она непрерывна в каждой точке этой области.

Для выполнения условия непрерывности (3) необходимо, чтобы:

1) функция f (х, у) была определена в точке М ₀ (х ₀ ,у ₀ );

2) существовал предел ;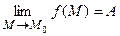

3) f (М ₀) = А.

Точка М₁(х₁,у₁) называется точкой разрыва функции f (х, у), если функция определена в окрестности этой точки, но в самой точке М₁ не выполнено хотя бы одно из указанных условий непрерывности.

Н епрерывность функции f (х, у) по совокупности аргументов не сводится к непрерывности по каждому аргументу в отдельности.

Определение непрерывности функции нескольких переменных f (М) (4) совершенно аналогично определению непрерывности функции одной переменной. Поэтому все свойства, установленные для непрерывных функций одной переменной, остаются в силе для непрерывных функций нескольких переменных:

1.Все элементарные функции нескольких переменных непрерывны в области определения.

2. Если функция f (М) непрерывна в замкнутой области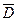, то она ограничена в ней (достигает наибольшего и наименьшего значения).

3. Непрерывная в 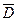функция, непрерывно переходя от одного своего значения к другому, необходимо проходит через каждое промежуточное значение.

Пусть функция z =f (х, у) определена и непрерывна в точке М ₀(х ₀, у ₀) и ее некоторой окрестности. Фиксируем значение у = у ₀, а изменять будем х.

М ₂

М ₁

М ₀

у ₀+D у

у ₀

М ₂

М ₁₀₁

М ₀

у ₀+D у

у ₀

ух

ух

Получим функцию одной переменной z =f (х, у ₀). Пусть М ₁(х + D х, у ₀). Рассмотрим разность

D_х z = f (М ₁ ) - f (М ₀ )= f (х + D х, у ₀ ) - f (х ₀ ,у ₀ ).

Эта разность называется частным приращением функции z

х ₀

х ₀+D х

х ₀

х

х ₀+D х

х

по переменной х: D _х z.

Рис. 8.

Если существует предел отношения при Dх®0, то этот предел называется частной производной функции z по переменной х в точке М₀ (х₀, у₀).

Обозначается , , , .

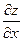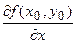Таким образом, по определению 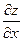=или =

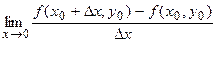
В определении частной производной не все координаты равноправны: у – фиксирован, а х изменяется. Точно так же при перемещении из точки М ₀(х ₀, у ₀) в точку М ₂(х ₀, у ₀ +D у) получим частное приращение функции z по переменной у (фиксировано х = х ₀, а у изменяется: z= f (х ₀, у)).

D _y z = f (М ₂) - f (М ₀) = f (х ₀ ,y ₀ + D у) - f (х ₀ ,у ₀)

Предел отношения при Dу®0, если он существует, называется частной производной функции z по переменной у.

Обозначается , , , .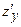

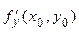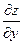По определению 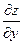= 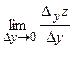или =.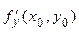

Отношение дает среднюю скорость изменения функции z по аргументу х на отрезке М ₀ М ₁, а отношение дает среднюю скорость изменения функции z по аргументу у на отрезке М ₀ М ₂.

Частные производные 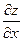и 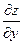характеризуют скорость изменения функции z в точке М₀ (х₀, у₀) в направлении координатных осей Ох и Оу.

Из определения частных производных следует и правило их вычисления: например, частная производная функции z =f (х, у) по переменной х находится так же, как и обыкновенная производная, считая у =const. Наоборот, частная производная функции z =f (х, у) по переменной у находится так же, как и обыкновенная производная, считая х =const.

Поэтому при вычислении частных производных сохраняют силу правила и формулы дифференцирования, доказанные для функции одной переменной.

Пример 1. .

= , =

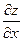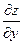Точно также определяются частные производные для функций большего числа переменных. Например, для n= 3:

u= f (x,y,z) и

=;

=; =.

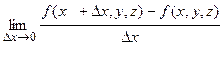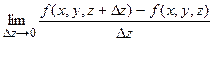По аналогии с функциями одной переменной можно для частных приращений функции f (x,y) ввести понятие частного дифференциала:

D _х z = ; d_х z = и

D_y z = ; d_y z = .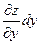

d_х z и d_y z – главная часть соответствующих частных приращений функции f (x,y).

Замечание. Для функции у = f (x) существование производной f¢ (x ₀) гарантирует непрерывность функции f (x) в точке х =х ₀. Для функции n ³ 2 переменных из существования частных производных по всем переменным в точке М ₀не следует непрерывность функции u= f (М) в этой точке.

Существование частных производных в точке М ₀ означает, что функция удовлетворяет определенным условиям в направлении координатных осей. Для непрерывности необходимо выполнение некоторых условий по всем направлениям.

Дата добавления: 2014-01-14