Вычисление площади плоских фигур

Не вдаваясь в детали, будем считать, что все рассматриваемые ниже множества имеют площадь и объем. Изложенная выше схема позволяет в ряде случаев получить формулы для вычисления площади.

Теорема 1. Пусть и , .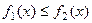

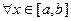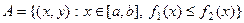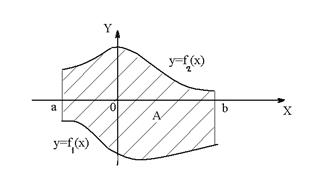
Площадь 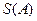множества А вычисляется по формуле

.

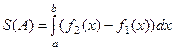Теорема 2. Пусть , , , .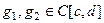

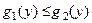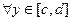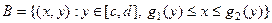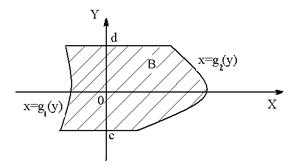
Площадь 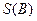множества 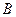вычисляется по формуле

.

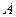Множества и 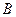называются криволинейными трапециями.

24) Вычисления объема тела по поперечным сечениям.

Будем вычислять объем тела, расположенного между двумя параллельными плоскостям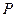и и .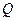

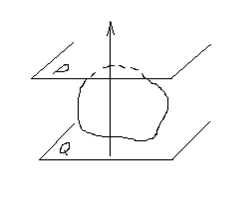
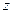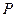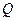Проведем ось перпендикулярно плоскостям и . При 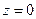получаем плоскость 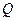, при 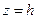- плоскость 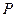. Будем считать также, что известна 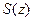- площадь сечения тела плоскостью 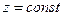. Для нахождения объема тела разобьем отрезок 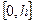точками , и через точки 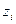проведем плоскости, параллельные плоскостям 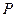и 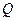. Объем слоя, заключенного между 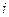- ой и 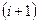-ой плоскостями можно считать приближенно равным 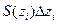, а объем всего тела - 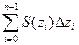. Это приближенное значение будет тем точнее, чем меньше 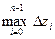, поэтому объем тела .

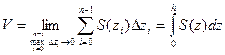Из этой формулы следует принцип Кавальери: если два тела, расположенные между двумя параллельными плоскостям 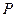и 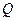таковы, что в сечении этих тел любой плоскостью, параллельно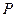й и 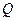, получаются равновеликие фигуры, то и объемы этих тел равны.

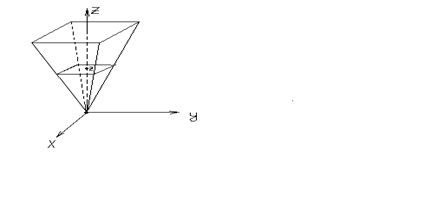Пример 1. Найдите объемправильной четырехугольной пирамиды.

Решение. Поставим пирамиду на вершину, а ось симметрии пирамиды направим по оси 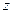. Пусть высота пирамиды равна 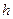, а основание ее, оказавшееся сверху, представляет собой квадрат со стороной . Сечение пирамиды плоскостью на высоте 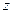есть квадрат со стороной 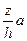. Поэтому 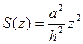, и .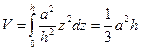

Пример 2. Определите объем цилиндрического копыта (части прямого кругового цилиндра, отсекаемого от него проходящей через диаметр основания плоскостью, образующей с основанием угол ).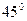

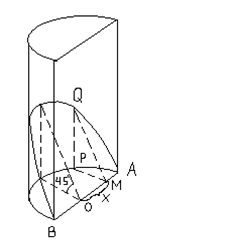Решение. Радиус цилиндра для простоты примем равным 1. Сечение копыта плоскостью, перпендикулярной диаметру 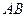и удаленной оси центра на расстояние 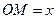, представляет собой прямоугольный равнобедренный треугольник, катет которого равен 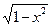. Тогда 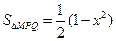. Поэтому .

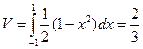Дата добавления: 2014-11-06