Расчет межгрупповой дисперсии

Группы предприятий по стоимости основных производствен-ных фондов, млн.руб.	Число пред-приятий   f	Объем продукции в среднем на одно предприятие, млн. руб.
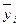
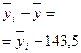
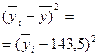
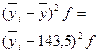
10-22		56,0	-87,5	7656,25	22968,75
22-34		88,3	-55,2	3047,04	27423,36
34-46		138,0	-5,5	30,25	151,25
46-58		159,0	15,5	240,25	720,75
58-70		328,5	185,0	34225,0	136900,0
Итого		143,5	-	-	188164,1

Общая средняя 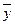была определена ранее (см. пример 1 разд.1):

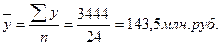
Определим дисперсию, характеризующую вариацию выпуска продукции за счет изменения основных фондов, т.е. межгрупповую дисперсию. Межгрупповая дисперсия равна:

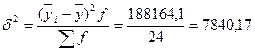
Исчислим общую дисперсию по индивидуальным данным результативного признака (у) таблицы 1.1, используя формулу:

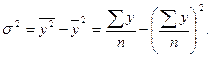
Таблица 3.8

Расчет среднего значения квадрата индивидуального признака «У»

№ предприятия	y	y ^2	№ предприятия	y	y ^2
Итого

Общая дисперсия равна:

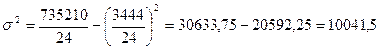
Коэффициент детерминации равен:

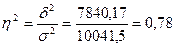0.

Корреляционное отношение равно:

.

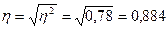Таким образом, можно сказать, что связь между размером основных фондов и выпуском продукции в рассмотренном примере высокая. Коэффициент детерминации, равный 0,780 или 78,0%, означает, что выпуск продукции на 78,0% зависит от стоимости фондов (определяется стоимостью фондов).

РАЗДЕЛ 4. КОРРЕЛЯЦИОННАЯ СВЯЗЬ И ЕЕ СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ

Методические указания и решение типовых задач

Социально – экономические явления представляют собой результат одновременного воздействия большого числа причин. При изучении этих явлений необходимо выявлять главные, основные причины, абстрагируясь от второстепенных. При изучении конкретных зависимостей одни признаки выступают в качестве факторов (факторные признаки), обуславливающих изменение других признаков. Признаки, изменяющиеся под воздействием факторных признаков, называют результативными.

Связи между явлениями и их признаками классифицируются по степени тесноты (слабые, сильные), по направлению (прямые, обратные) и по аналитическому выражению (линейные, нелинейные).

В корреляционном анализе для выявления наличия или отсутствия корреляционной связи используется ряд специфических методов:

• параллельное сопоставление рядов значений факторного и результативного признаков (анализ параллельных рядов);
• графическое изображение фактических данных с помощью поля корреляции;
• построение групповой и корреляционной таблиц;
• дисперсионный анализ (см. тему «Виды дисперсий»).

Метод анализа параллельных рядов заключается в том, что полученные в результате сводки и обработки материалы располагаются в виде параллельных рядов факторного и результативного признаков и сопоставляют их между собой для установления характера и тесноты связи. Для этого используют разные показатели. Простейшим из них считается коэффициент корреляции знаков, или коэффициентГ. Фехнера. Для его расчета вычисляют средние значения обоих признаков и затем определяют знаки отклонений от средней для всех значений взаимосвязанных признаков. Приняв число совпадений знаков отклонений индивидуальных значений от средней за С, а число несовпадений – за Н, коэффициент запишем следующим образом:

.

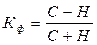Коэффициент Фехнера целесообразно использовать для установления факта наличия связи при небольшом объеме исходной информации. Он принимает значения от -1 до +1. Положительное его значение говорит о прямой связи, отрицательное – об обратной. Близость к нулю говорит о слабой связи, близость к 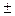1 говорит о существенной связи.

Рассмотрим расчет коэффициента Г. Фехнера на примере.

Пример 1. Имеются следующие данные о стаже работы и дневной выработке рабочих (табл.4.1). Необходимо установить наличие и характер связи. Предварительные расчеты для определения коэффициента Фехнера представлены в таблице 4.2.

Таблица 4.1.

Дата добавления: 2014-11-06