Ol — V2X 15 страница

dQ

т. V, и„

<°>> (ад

так что вычисление Q сводится к вычислению среднего значения <0>.

*) Определение понятия химических потенциалов компонент смеси—см. § 85.

Мы увидим, что в вырожденной слабо неидеальной плазме основную роль в поправках к термодинамическим величинам идеального газа играет обменная часть электрического взаимо­действия электронов (которая в классическом случае несущественна и в § 78 вовсе не учитывалась). Имея это в виду, будем писать в операторе U лишь члены, описывающие кулоновское взаимо­действие электоонов.

Вычисление <(У> наиболее просто осуществляется с помощью метода вторичного квантования. Следуя этому методу (см. III, §§ 64, 65), вводим систему нормированных волновых функций %_а, описывающих состояния свободных электронов, движущихся в объеме V с импульсами р и проекциями спина а (а = ±1/2). Импульс р пробегает бесконечный набор дискретных значений, интервалы между которыми стремятся к нулю при V—^оо. Далее вводим операторы а_9а и а^, уничтожения и рождения электронов в состояниях ifp_a, а с их помощью образуем ^-операторы

♦ = Z$Poflpe, Ф⁺=2%ойр⁺о. (80,5)

Кулоновское взаимодействие частиц имеет «парный» характер; оператор такого взаимодействия записывается в методе вторичного квантования в виде интеграла

^{0 =} Т И ^^{+ (ri)} *^{+ {Гг)} йГ=г7Т *^(Га) *^{(fl) dV}i^dV*- <⁸⁰'⁶⁾

Требуемое усреднение этого оператора производится в два этапа: сначала усреднение по заданному квантовому состоянию системы, а затем усреднение по равновесному статистическому распределению по различным квантовым состояниям. В слабо неидеальной плазме U играет роль малого возмущения. Вычислим среднее значение этой величины в первом приближении теории возмущений, другими словами—по отношению к состояниям системы невзаимодействующих частиц, т. е. идеального газа.

Квантовомеханическое усреднение сводится к взятию соответ­ствующего диагонального матричного элемента. После подстановки яр-операторов (80,5), оператор (80,6) представится в виде суммы членов, содержащих различные произведения операторов рождения и уничтожения, взятых по четыре:

# = у £ <р;р₂1 ^и I PiPa > K^Klo^fip^, (80,7)

где суммирование производится по всем импульсам и проекциям спина, a <p[pl\ £/₁₂|р_гр₂>—матричные элементы от энергии вза­имодействия двух электронов £/₁₂ = е²/1 г_х—г₂1; поскольку куло­новское взаимодействие не зависит от спинов, то эти элементы берутся для переходов без* изменения проекций спинов электро­нов, т. е. могут вычисляться по чисто орбитальным функциям

Из всех членов суммы (80,7) диагональные матричные эле­менты имеют лишь те, которые содержат две пары операторов

«ро, «ра с одинаковыми индексами, причем произведение ар₀а_р(, заменяется просто числом заполнения данного квантового состо­яния электронов¹). Положив р₁ = р[, Ра = р₂, получим члены

IF²" £ 2^пр^^пр.°,J ТгТ^гТГ' ⁽⁸°'⁸^

Pi Ф Рг <JiOj

а положив р1 = р₂, P2 = Pi. o"i = o"2,— члены

-шSH"p^J^el(p,"^P2)(r,'^r!Vfeif^r ⁽⁸⁰*⁹⁾

Pi Рг О

(знак минус возникает здесь в результате перестановки операто­ров a,p_i0 и а_Р2а, нужной для приведения произведения ap_l0ap_l<5ap_taa_Via к виду ap₂aap_l0a^_iaa_Pia; напомним, что в случае фермионов эти опе­раторы антикоммутативны).

Члены (80,8) представляют собой просто энергию прямого кулоновского взаимодействия электронов, равномерно распреде­ленных в пространстве. Как уже было отмечено в § 78, ввиду электрической нейтральности плазмы эти члены в действитель­ности тождественно сокращаются с аналогичными членами, выра­жающими энергию взаимодействия других частиц (ионов) друг с другом и с электронами (и в этой связи расходимость инте­грала в (80,8) несущественна). Члены же (80,9), содержащие недиагональные матричные элементы кулоновского потенциала, вы­ражают собой искомый обменный эффект⁸).

Имея в виду, что при макроскопическом объеме V импульсы электронов пробегают практически непрерывный ряд значений, можно перейти от суммирования по р₁₍ р₂ к интегрированию по Vⁱd³p₁d³p₂/(2nfty (при этом ограничение р^Рг становится несу­щественным). Интеграл в (80,9) равен³)

yC_cMP,-P.)r/fcgy ₌ y ^4пр

^г) Что касается членов с произведениями четырех операторов с одинако­выми индексами, то их число неизмеримо мало по сравнению с числом членов с двумя различными парами одинаковых индексов, и их поэтому не надо учи­тывать (вклад в Q от этих членов содержал бы лишнюю степень 1/V).

²) Для лучшего уяснения структуры членов (80,8) и (80,9), обратим вни-
мание на то, что в первых из них пары операторов а_ро, с одинаковыми ин-
дексами происходят от ^-операторов, взятых в одной и той же точке простран-
ства 0"i или г₂); в членах же (80,9) эти пары происходят от ф-операторов,
взятых в различных точках.

³) Здесь использовано известное выражение для фур ье-компоненты куло-
новского потенциала:

С JbdV_ 4л

у т—w

(см., ниже примечание на стр. 390).

В результате выражение (80,9) принимает вид -2ne*V У \ С ^!Г^Ч —Ф" •

^JJ (Pi —Р₂)^а (2л)°£*

Статистическое усреднение этого выражения производится (в рассматриваемом приближении) по равновесному распределению идеального газа. Ввиду статистической независимости частиц идеального _газа в различных квантовых состояниях при этом <rc_Plaip₂<r> = tt_Pl<jrtp₂a; средние же значения n_pa даются формулой распределения Ферми п_ра — [ е(^Е_^)/^г + 1 ]^-1 (р_е—химический по­тенциал электронов). Наконец, поскольку получившееся выражение просто пропорционально е², то, согласно (80,4), оно непосредственно дает искомую поправку к термодинамическому потенциалу плазмы:

Q_o6M„^fly(T "р."р. *PfP* (go.io)

fa JJ (Pi—Р_а)^а <^2д)

(£. Wigner, F. Seitz, 1934).

В предельном случае сильного вырождения электронного газа (Т <^tfi²n^2/s/m) распределение п_р сводится к «ступенчатой» функ­ции (п_р = 1 при р < p_F, rip = 0 при р > р_Р). Вычисление инте­грала приводит тогда к результату¹):

°-—<^8WI>

Эта же величина, если выразить в ней химический потенциал через плотность числа электронов п_е = N_ejV (согласно (57,3)) дает поправку к свободной энергии:

F₀6_M = -N_e^e*nl^/3. (80,12)

^х) Интеграл

РъР*<Рр,

заменой Pi—p₂ = q. (Pi + P2)/^{2 = s} приводится к интегралу / = q-²d³qd³s,

берущемуся по области | s ± q/2 К р_Р.Интеграл Jd³s (при заданном q)есть

объем, заключенный между двумя сферами радиуса p_F с центрами, раздвину­тыми на расстояние q:

I

d³s = ^-h²(3p_F-h), h = p_F-±

Интегрируя затем по d?q по области 0 < q < 2p_F, получим /=4я²р£.

В обратном же предельном случае больцмановского газа (ц_е < 0, p-el^T) вычисление по формуле (80,10) дает¹)

⁰-=-О^>,/г <^80ЛЗ>

или, выразив (х_е через п_е согласно (46,1а),

F_o6M = -V^-. (80,14)

При Т ~ц_е обменная поправка F_o6vi~Ve²n*l³, между тем как найденная в § 78 корреляционная поправка f_kopp ~ Ve³n^²jT¹^²; при этом в силу условия слабой неидеальности

Лшрр /^„1/3 \ 1/2

^обм

т. е. электронная обменная поправка действительно является главной. При повышении температуры, однако, F_o6m убывает быстрее, чем F_KOpp (при T^\i_e:F_o6yi со Т'¹, a F_KOppсо Т'¹'²). Поэтому существует область, в которой обе поправки одинакового порядка величины. В этой области, однако, вырождение плазмы уже незначительно, и потому для корреляционной поправки можно пользоваться классическими формулами (78,11—14)^а).

В предыдущем изложении подразумевалось, что ионная ком­понента плазмы не только не вырождена, но и почти идеальна, т. е. что энергия взаимодействия ионов мала по сравнению с их тепловой энергией: п^1/3е² <^Т³). Но если плотность плазмы не слишком велика:

^_<п,,_а<™(80,15)

(М—масса иона), то температура Т ~ п>1³е^% превышает темпера­туру вырождения ионов:

T~eW³^>-!^— (80,16)

¹)В этом случае ^га_р1^лр,-^ехР \ _т 2шТ /-^ехр\ Т АпгТ ] и интегрирование по d?sd³q распространяется по всему q- и s-пространству. ²)Вопрос о вычислении корреляционной поправки при произвольной степени вырождения электронов представляет, тем не менее, определенный методический интерес. Эта задача будет рассмотрена в другом томе этого курса (том IX). ^а) В этой и последующих оценках полагаем для простоты 2=1 (водород­ная плазма).

(причем Т<^.е¹М/%²). В этих условиях ионная компонента состав­ляет невырожденную, но существенно неидеальную систему.

Минимальности энергии взаимодействия ионов друг с другом и с электронами отвечает тогда упорядоченное расположение ядер, т. е. ядра образуют кристаллическую решетку (А. А. Абрико­сов, 1960). Это приводит к тому, что энергии прямого кулонов­ского взаимодействия различных частиц уже не полностью взаимно компенсируются. В каждой ячейке решетки поле ионов компен­сируется находящимися в ней электронами. Но энергия взаимо­действия частиц в пределах одной ячейки (размеры которой ~п~¹¹³) отлична от нуля. По грубой оценке эта энергия ~е²п^1/3, а для всей решетки (с числом ячеек N ~ Vn) ее энергия связи состав­ляет

I £_Реш I ~ NeW³ ~ VeW³. (80,17)

i) Количественное вычисление энергии связи решетки —см. А. А. Абрикосов ЖЭТФ, 39, 1797 (1960).

По порядку величины она совпадает с обменной энергией выро­жденной электронной компоненты плазмы. Для устойчивой решетки энергия связи, разумеется, отрицательна¹).

ГЛАВА VIII

РАВНОВЕСИЕ ФАЗ

§ 81. Условия равновесия фаз

Состояние (равновесное) однородного тела определяется зада­нием каких-либо двух термодинамических величин, например объема V и энергии Е. Однако нет никаких оснований утверждать, что при всякой заданной паре значений V и Е тепловому равно­весию будет соответствовать именно однородное состояние тела. Может оказаться, что при данных объеме и энергии в тепловом равновесии тело не является однородным, а распадается на две соприкасающиеся однородные части, находящиеся в различных состояниях.

Такие состояния вещества, которые могут существовать одно­временно в равновесии друг с другом, соприкасаясь между собой, называются различными фазами вещества.

Напишем условия равновесия двух фаз друг с другом. Прежде всего, как и для любых находящихся в равновесии тел, должны быть равны температуры Т_х и T_t обеих фаз:

Далее должно выполняться условие равенства давлений в обеих
фазах: р _ р

поскольку на поверхности их соприкосновения силы, с которыми обе фазы действуют друг на друга, должны быть равны и про­тивоположны.

Наконец, должно выполняться условие равенства химических потенциалов обеих фаз:

которое выводится для двух фаз в точности тем же образом, как это было сделано в § 25 для любых двух соприкасающихся участков тела. Если потенциалы выражены как функции от дав­ления и температуры, то, обозначая равные друг другу темпера­туры и давления обеих фаз через Т и Р, мы получим уравнение

МЛ Т) = ц.₂ (Р, Т), (81,1)

откуда давление и температура находящихся в равновесии фаз могут быть выражены как функции друг друга. Таким образом, две фазы могут находиться в равновесии друг с другом не при любых давлении и температуре; задание одной из этих величин вполне определяет вторую.

Если откладывать на осях координат давление и температуру, то точки, в которых возможно равновесие фаз, будут лежать на некоторой кривой (кривой равновесия фаз). При этом точки, ле­жащие по сторонам этой кривой, будут представлять собой одно­родные состояния тела. При изменении состояния тела вдоль линии, пересекающей кривую равновесия, наступает расслоение фаз (в точке пересечения кривой), после чего тело переходит в другую фазу. Заметим, что при медленном изменении состояния тела оно иногда может остаться однородным даже тогда, когда при полном равновесии уже должно было бы наступить разделение фаз (таковы, например, переохлажденный пар и перегретая жид­кость). Такие состояния, однако, метастабильны.

Если изображать равновесие фаз с помощью диаграммы, в ко-
торой на осях координат откладываются температура и объем
(отнесенный к определенному количеству вещества), то состояния,
j-i в которых имеются одновременно две

* фазы, будут заполнять целую область

плоскости, а не только одну кривую;

_о _______________ это отличие от диаграммы Р, Т свя-

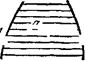
* 1 * ' V ^ ^{зано с тем}> ^чт0 объем V в противопо­ложность давлению неодинаков у обеих фаз. В результате получается диаграмма изображенного на рис. 12 типа. Точки в областях I и II по обе стороны заштрихованной обла-

у сти соответствуют однородным пер-
Рис. 12. вой и второй фазам. Заштрихован-

ная же область изображает состоя­ния, в которых обе фазы находятся в равновесии друг с другом: в какой-либо точке а находятся в равновесии фазы / и II с удельными объемами, определяемыми абсциссами точек 1 и 2, лежащих на горизонтальной прямой, проходящей через точку а. Непосредственно из баланса количества вещества легко заклю­чить, что количества фаз I и II при этом обратно пропорцио­нальны длинам отрезков al и а2 (так называемое правило рычага).

Аналогично условиям равновесия двух фаз, равновесие трех фаз одного и того же вещества определяется равенствами

/>! = />, = />„ 7^,₁ = 7'₁ = 7'„ р₁ = р₂ = р₃- (81,2)

Если обозначить снова общие значения давления и температуры трех фаз посредством Р и Т, то мы получим условия

1*,(Л71 = С.(Л7^,) = |1,(Л Г). (81,3)

Это—два уравнения с двумя неизвестными Р и Т; они имеют в качестве решений определенные пары значений Р и Т. Состоя­ния, в которых одновременно существуют три фазы (так называе­мые тройные точки), на диаграмме Р, Т изобразятся изолиро­ванными точками, являющимися точками пересечения кривых равновесия каждых двух из трех фаз (рис. 13; области /, //, ///—области трех однородных фаз). Равновесие более чем трех фаз одного и того же вещества, очевидно, невозможно.

На диаграмме Т, V окрестность тройной точки имеет вид, изображенный на рис. 14, где заштрихованные области—области попарного равновесия фаз; удельные объемы трех фаз, находящихся в равновесии в тройной точке (при температуре Т_Т9), определяются абсциссами точек /, 2, 3.

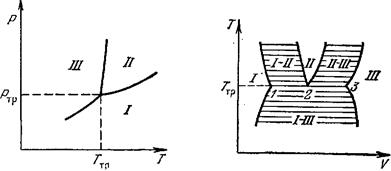
Рис. 13. Рис. 14.

Переход из одной фазы в другую сопровождается выделением или поглощением некоторого количества тепла (теплота перехода). Согласно условиям равновесия такой переход происходит при постоянных давлении и температуре. Но при процессе, протекаю­щем при постоянном давлении, количество поглощаемого телом тепла равно изменению его тепловой функции. Поэтому теплота перехода, отнесенная к одной молекуле, есть

q = w_t—w_lt (81,4)

где w_l и w₂—тепловые функции обеих фаз, отнесенные к одной молекуле. Величина q положительна, если при переходе из первой фазы во вторую тепло поглощается, и отрицательна, если при этом переходе тепло выделяется.

Поскольку ц (для тел, состоящих из одного вещества) есть термодинамический потенциал на одну молекулу, то можно на­писать: [л = е — Ts + Pv (г, s, v—молекулярные энергия, энтропия и объем). Поэтому условие ц₁ = и.₂ дает

(ез-ej - Т (s₂-_Sl) + Р (v,—_Vl) = К-oij - Т (8,-sJ - О, где Т и Р—температура и давление обеих фаз, откуда

q = T(s_a-_Sl). (81,5)

Заметим, что эта формула вытекает и непосредственно из того, что q=^Tds, а температура постоянна (эта формула применима здесь, так как переход совершается обратимо—обе фазы во время перехода остаются в равновесии друг с другом).

Пусть две кривые на рис. 15 изображают химические потен­циалы двух фаз как функции температуры (при заданном давле­нии). Точка пересечения обеих кривых определяет температуру Т₀,

при которой (при данном давлении) обе
фазы могут находиться в равновесии друг
с другом. При всех остальных темпера-
турах может существовать либо одна, либо
другая фаза. Легко видеть, что при тем-
пературах ниже Т_а существует, т. е. яв-
ляется устойчивой, первая фаза, а при
температурах выше Го—вторая. Это сле-
дует из того, что устойчиво то состояние,
в котором р меньше (так как термодинами-
Рнс. 15. ческий потенциал стремится при заданных

Я и Г к минимуму). С другой стороны, в точке пересечения обеих кривых значение производной d\nJdT больше, чем значение др₃/дТ, т. е. энтропия первой фазы s₁ = — dnJdT меньше, чем энтропия второй s₂ =— d\i₂/dT. По­этому теплота перехода q = T(s₂—sj положительна. Таким обра­зом, мы приходим к выводу, что если при повышении темпера­туры тело переходит из одной фазы в другую, то при этом тепло поглощается. Этот результат можно было бы получить и из прин­ципа Ле-Ш ателье.

Задачи

1. Определить температурную зависимость давления насыщенного пара над твердым телом (пар рассматривать как идеальный газ; как газ, так и твердое тело обладают постоянными теплоемкостями).

Решение. Химический потенциал пара определяется формулой (43,3), а твердого тела—формулой (65,6) (ввиду относительной малости давления насыщенного пара можно для твердого тела пренебречь величиной PV и счи­тать Ф равным F). Приравнивая оба выражения, найдем

P=const-r^(C/^,2~^C'^,e^(E»'-^e»»^)/T,

где индекс 1 относится к твердому телу, 2— к пару.

В том же приближении тепловую функцию твердого тела можно считать равной его энергии; теплота перехода (теплота возгонки) q*=w₂—w_x равна

Ч=(<>*—^сд ^Т + (^еп — ^еп>-

В частности, теплота перехода при Г = 0 есть 9₀ = ^ее2— ^Eoi> так что можно

написать: Р = const-T^'7>а~^С1)_e-^q'^/T'.

2. Определить скорость испарения конденсированного тела в пустоту.

Решение. Скорость испарения в пустоту определяется числом частиц, покидающих в единицу времени единицу площади поверхности тела. Рассмотрим тело, находящееся в равновесии со своим насыщенным паром. Тогда число частиц, покидающих поверхность тела, равно числу частиц, падающих в течение того же времени на эту поверхность и «прилипающих» к ней, т. е. равно

^Ро - -(1-Я),

У"2лтТ

где Р₀=Р₀ (Т) —давление насыщенного пара, a R — некоторый средний коэф­фициент отражения частиц газа, сталкивающихся с поверхностью тела (см. (39,2)). Если Р₀ не слишком велико, то число частиц, покидающих поверхность тела, не зависит от того, имеется ли в окружающем пространстве пар или нет, так что написанное выражение определяет искомую скорость испарения в пустоту.

§ 82. Формула Клапейрона — Клаузиуса

Продифференцируем обе стороны условия равновесия

l*i (Л Л = 1*.(Л Т)

по температуре. При этом, разумеется, надо помнить, что давле­ние Р — не независимая переменная, а функция температуры, определяемая этим самым уравнением. Поэтому пишем:

дщ. дцх dP __ дц₂. дц₂ dP дТ ~г дР dT~ дТ ' дР dT '

и, поскольку (дц,/дТ)_р = — s, (d\i/dP)_T = v (см. (24,12)), получаем

dT

dP s-i — So

(82,1)

где s_lt v_x и s₂, v₂—молекулярные энтропии и объемы обеих фаз.

В этой формуле разность s_t—s₂ удобно выразить через те­плоту перехода из одной фазы в другую. Подставляя q = Т (s₂—Sj), находим формулу Клапейрона—Клаузиуса •

dT ⁼ Т (t>₂—• (^82,2)

Она определяет изменение давления находящихся в равновесии фаз при изменении температуры, или, другими словами, измене­ние давления с температурой вдоль кривой равновесия фаз. Та же формула, написанная в виде

dT _ T(v₂—t>t) dP~ q»

определяет изменение температуры перехода между двумя фазами (например, точки замерзания или кипения) при изменении давле­ния. Так как молекулярный объем газа всегда больше объема жидкости, а при переходе жидкости в пар тепло поглощается, то, следовательно, температура кипения при увеличении давления всегда повышается (dT/dP > 0). Точка же замерзания при уве­личении давления повышается или понижается, смотря по тому, увеличивается или уменьшается объем при плавлении¹).

Все эти следствия формулы (82,2) находятся в полном согласии с принципом Ле-Шателье. Рассмотрим, например, жидкость, на­ходящуюся в равновесии со своим насыщенным паром. Если увеличить давление, то температура кипения должна повыситься, вследствие чего часть пара перейдет в жидкость, что в свою очередь повлечет за собой уменьшение давления, т. е. система как бы противодействует выводящему ее из равновесия воздей­ствию.

Рассмотрим частный случай формулы (82,2), когда речь идет о равновесии твердого или жидкого тела с его паром. Формула (82,2) определяет тогда изменение давления насыщенного пара с температурой.

Объем газа обычно значительно больше объема конденсирован­ного тела, содержащего столько же частиц. Поэтому мы можем пренебречь в (82,2) объемом v_x по сравнению с объемом i>₂ (мы считаем второй фазой газ), т. е. принять dPjdT = q/Tv₂. Рассмат­ривая пар как идеальный газ, выразим его объем через давление

dP аР

и температуру согласно формуле v₂ = T/P; тогда ^ = -f2-> или

dlnP _ q ■,_л0 о.

Отметим, что в интервалах температуры, в которых теплоту пе­рехода можно считать постоянной, давление насыщенного пара меняется с температурой по экспоненциальному закону ~ехр (—q/T).

Задачи

1. Определить теплоемкость пара вдоль кривой равновесия жидкости и ее насыщенного пара (т. е. теплоемкость для процесса, при котором жидкость все время находится в равновесии со своим насыщенным паром). Пар считается идеальным газом.

Решение. Искомая теплоемкость h равна

h = T^-dT '

где dsjdT — производная вдоль кривой равновесия, т. е.

^г) Исключение представляет жидкий изотоп гелия, Не³, для которого в определенном интервале температур теплота плавления отрицательна.

Подставляя для dP/dT выражение (82,3) и v=T/P, находим

При низких температурах h отрицательно, т. е. если отнимать тепло так, чтобы пар все время был в равновесии с жидкостью, его температура может повы­шаться.

2. Определить изменение объема пара с температурой для процесса, при котором пар все время находится в равновесии с жидкостью (т. е. вдоль кривой равновесия жидкости и ее пара).

Решение. Надо определить производную dv/dT вдоль кривой равновесия:

do__(dv_\,(dv\ dP dT~\dT j_p' \dP)xdT '

Подставляя (82,3) и v = T/P, находим

dT P \ T) •

При низких температурах dv/dT < 0, т. е. при рассматриваемом процессе объем пара уменьшается с увеличением температуры.

§ 83. Критическая точка

Кривая фазового равновесия (в плоскости Р, Т) может в не­которой точке окончиться (рис. 16); такая точка называется кри­тической, а соответствующие ей температура и давление—кри­тической температурой и критическим давлением. При темпера­турах выше Г_кр и при давлениях, больших Р_кр, не существует

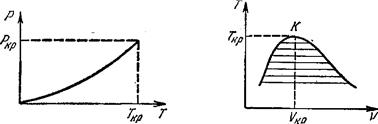
Рис. 16. Рис. 17.

различных фаз, и тело всегда однородно. Можно сказать, что в критической точке исчезает различие между обеими фазами. Понятие о критической точке было впервые введено Д. И. Мен­делеевым (1860).

В координатах Т, V диаграмма равновесия при наличии кри­тической точки выглядит так, как это изображено на рис. 17. По мере приближения температуры к ее критическому значению удельные объемы находящихся друг с другом в равновесии фаз сближаются и в критической точке (К на рис. 17) совпадают. Аналогичный вид имеет диаграмма в координатах Р, V.

При наличии критической точки между всякими двумя состоя­ниями вещества может быть произведен непрерывный переход, при котором ни в какой момент не происходит расслоения на две фазы—для этого надо менять состояние вдоль какой-либо кривой, огибающей критическую точку и нигде не пересекающей кривую равновесия. В этом смысле при наличии критической точки становится условным самое понятие о различных фазах, и невозможно во всех случаях указать, какие состояния яв­ляются одной фазой, а какие—другой. Строго говоря, можно говорить о двух фазах лишь тогда, когда они существуют обе одновременно, соприкасаясь друг с другом, т. е. в точках, лежа­щих на кривой равновесия.

Ясно, что критическая точка может существовать лишь для таких фаз, различие между которыми имеет лишь чисто количе­ственный характер. Таковы жидкость и газ, отличающиеся друг от друга лишь большей или меньшей ролью взаимодействия между молекулами.

Такие же фазы, как жидкость и твердое тело (кристалл) или различные кристаллические модификации вещества, качественно различны между собой, так как отличаются своей внутренней симметрией. Ясно, что о всяком свойстве (элементе) симметрии можно сказать только либо, что оно есть, либо, что его нет; оно может появиться или исчезнуть лишь сразу, скачком, а не постепенно. В каждом состоянии тело будет обладать либо одной, либо другой симметрией, и потому всегда можно указать, к ко­торой из двух фаз оно относится. Критическая точка, следова­тельно, для таких фаз не может существовать, и кривая равно­весия должна либо уходить на бесконечность, либо заканчи­ваться, пересекаясь с кривыми равновесия других фаз.

Обычная точка фазового перехода не представляет собой в математическом отношении особенности для термодинамических величин вещества. Действительно, каждая из фаз может суще­ствовать (хотя бы как метастабильная) и по другую сторону от точки перехода; термодинамические неравенства в этой точке не нарушаются. В точке перехода химические потенциалы обеих фаз равны друг другу: \1_г(Р, T) = \i_t(P, Т); для каждой же из функ­ций р_х (Р, Т) и р_а (Р, Т) эта точка ничем не замечательна ^J).

^г) Надо, однако, отметить известную условность этих утверждений, связан­ную с некоторой неопределенностью понятия \и(Р, Т) в области метастабиль-ности. Метастабильное состояние представляет собой неполное равновесие, обла­дающее некоторым временем релаксации—в данном случае по отношению к процессу образования зародышей новой фазы (см. § 162). Поэтому термоди­намические функции в таком состоянии могут определяться лишь без учета этих процессов, и их нельзя рассматривать как аналитическое продолжение функций из области стабильности, отвечающей полностью равновесным состоя­ниям вещества.

Дата добавления: 2014-11-07