Ol — V2X 14 страница

Имея в виду, что согласно определению (75,3) dl/дц = ЦТ, получим

Л^Х-^гЕ». (75,6)

Два уравнения (75,4) и (75,6) определяют в параметрическом виде (параметр |) связь между Р, V и Т, т. е. уравнение состо­яния газа. Исключая из них £, можно получить уравнение состо­яния в виде ряда (75,1) с любым желаемым числом членов¹).

§ 76. Формула ван-дер Ваальса

В газах взаимодействие между молекулами весьма слабо. По мере его усиления свойства газа все больше отклоняются от свойств идеальных газов, и в конце концов газ переходит в кон­денсированное тело—жидкость. В последней взаимодействие между молекулами велико, и свойства этого взаимодействия (а потому и свойства жидкости) сильно зависят от конкретного рода

^х) В первом приближении Р=Т1, N = V\, откуда Р = NTJV=Р_Нд- Во втором приближении

NT N²T V 2V^{2 2}*

исключая из этих равенств £ (с той же точностью), получим что совпадает с (74,6).

жидкости. По этой причине невозможно, как уже указывалось, установить какие-либо общие формулы, которые бы количественно описывали свойства жидкости.

Можно, однако, найти некоторую интерполяционную формулу, качественно описывающую переход между жидкостью и газом. Эта формула должна давать правильные результаты в двух пре­дельных случаях. Для разреженных газов она должна переходить в формулы, справедливые для идеальных газов. При увеличении же плотности, когда газ приближается к жидкости, она должна учитывать ограниченную сжимаемость вещества. Такая формула будет тогда качественно описывать поведение газа и в промежу­точной области.

Для вывода такой формулы исследуем более подробно откло­нение от идеальности при высоких температурах. Как и в пре­дыдущих параграфах, будем сначала рассматривать одноатомный газ; по тем же соображениям, что и ранее, все получающиеся формулы будут в равной степени применимы и к многоатомным газам.

Описанный в § 74 характер взаимодействия атомов газа (рис. 11) позволяет определить вид первых членов разложения В (Т) по степеням обратной температуры; при этом мы будем считать ма­лым отношение

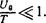
(76Д)

Имея в виду, что и_га есть функция только расстояния г меж­ду атомами, пишем в интеграле (74,5) dV = 4nr'dr. Разбивая область интегрирования по dr на две части, пишем:

В(Т) = 2пJ(1 —е~^и

о

»'^т)г*dr + 2пI(1 — е~^и^^т) г*dr.

Но при значениях г между О и 2г₀ потенциальная энергия U_lt в общем очень велика. Поэтому в первом интеграле можно пре­небречь членом ехр(—U₁₂/T) по сравнению с единицей. То­гда этот интеграл становится равным положительной величине Ь — 16лгЦЗ (если для одноатомного газа рассматривать г₀ как радиус атома, то Ь есть его учетверенный объем). Во втором интеграле везде (1/_1а|/Г<(7_в/Г<^1. Поэтому можно разложить подынте­гральное выражение в нем по степеням U\JT, ограничившись первым неисчезающим членом. Тогда второй интеграл становит­ся равным

-£S l«/i.l'^e*-~

2а Т ¹

где а—положительная постоянная. Таким образом, находим, что

В(Т) = Ь^-± (76,2)

Подставив это выражение в (74,4) и (74,7), находим свобод­ную энергию газа

F = F„ + -^-(bT-a) (76,3)

и его термодинамический потенциал

<D = a>_M + Jv7>(ft-f). (76,4)

Искомую интерполяционную формулу можно получить из формулы (76,3), которая сама по себе не удовлетворяет необхо­димым условиям, так как не учитывает ограниченную сжима­емость вещества. Подставим в (76,3) выражение для р_ия из (42,4). Мы получим тогда

F = Nf(T)—JVTln-^-—NT (inV—у-) • (76,5)

При выводе формулы (74,4) для свободной энергии газа мы пред­полагали, что газ, хотя и недостаточно разрежен для того, чтобы считаться идеальным, однако все же имеет достаточно большой объем (так, чтобы можно было пренебречь тройными и т. д. стол­кновениями молекул), т. е. расстояния между молекулами в общем значительно больше, чем их размеры. Можно сказать, что объем V газа во всяком случае значительно больше чем Nb. Поэтому

}n(V-Nb) = lnV + \n(l-y.)»taV—^. Следовательно, (76,5) можно написать в виде F^Nfi^ — NTln-^-iV—Nb)—^ =

= ^-iVTln(l-f)-^. (76,6)

В таком виде эта формула удовлетворяет поставленным выше условиям, так как при больших V она переходит в формулу для свободной внергии идеального газа, а при малых V она обнару­живает невозможность беспредельного сжатия газа (при V < Nb аргумент логарифма делается отрицательным).

Зная свободную энергию, можно определить давление газа:

OF NT та

или

(p+~-)(V-Nb)^NT. (76,7)

Это и есть искомое интерполяционное уравнение состояния реаль­ного газа—уравнение ван-дер-Ваальса. Разумеется, оно является лишь одной из бесчисленных возможных интерполяционных фор­мул, удовлетворяющих поставленным требованиям, и нет никаких физических оснований для выбора одной из них. Формула ван-дер-Ваальса является лишь наиболее простой и удобной'). Из (76,6) можно найти энтропию газа

S = S„_e +.iVln(l-^), (76,8)

а затем его энергию Е = F-\-TS.

Е = Е_ЯЛ-^. (76,9)

Отсюда видно, что теплоемкость C_v = (dE/dT)_v ван-дер-ваальсов-ского газа совпадает с теплоемкостью идеального газа, она зави­сит только от температуры и, в частности, может быть постоян­ной. Теплоемкость же С_р, как легко убедиться (см. задачу 1), зависит не только от температуры, но и от объема, и потому не может сводиться к постоянной.

Второй член в (76,9) соответствует энергии взаимодействия молекул газа; он, естественно, отрицателен, так как между моле­кулами в среднем преобладают силы притяжения.

Задач и

1. Найти С_р—C_v для неидеального газа, описываемого формулой ван-дер-
Ваальса.

Решение. С помощью формулы (16,10) и уравнения ван-дер-Ваальса находим:

С —С ^N

2. Найти уравнение адиабатического процесса для ван-дер-ваальсовского
газа с постоянной теплоемкостью C_v.

Решение. Подставляя в (76,8) S_ajl = N In V-\-Nc_v In Г (несущественные постоянные опускаем) и приравнивая S постоянной, найдем соотношение

¹) При конкретном применении этой формулы значения постоянных а и 6 следует выбирать так, чтобы получить наилучшее согласие с опытом. Постоян­ную Ь при этом уже отнюдь нельзя рассматривать как учетверенный объем молекулы,— даже в случае одноатомного газа.

(V—Nb) T^Cv=* const.

Оно отличается от соответствующего уравнения для идеального газа заменой V на V—Nb.

3. Для такого же газа найти изменение температуры при расширении в
пустоту от объема V_t до объема V₂.

Решение. При расширении в пустоту остается постоянной энергия газа. Поэтому из формулы (76,9) (с £_Ha = A⁷C_t,T) находим

_{т т} Na (1 1

^Ti-^Tl=-c7{T;-v;

4. Для ван-дер-ваальсовского газа найти зависимость точки инверсии процес-
са Джоуля—Томсона от температуры.

Решение. Точка инверсии определяется равенством (dT/dV)p =T/V (см. (74,9)). После подстановки Т из (76,7) оно дает уравнение, которое должно быть решено совместно с (76,7). Алгебраическое вычисление приводит к сле­дующей зависимости точки инверсии от давления:

г„-$(,_±]Л=5!

При каждом давлении Р < а/36³ имеется две точки инверсии, между которыми производная (дТ/дР)^ положительна, а вне этого интервала температур от­рицательна. При Р > а/36² точки инверсии отсутствуют и везде (dTjdP)_w < О¹).

§ 77. Связь вириального коэффициента с амплитудой рассеяния

При вычислении вириальных коэффициентов в §§ 74—76 мы исходили из классической статистики, что практически всегда оправдано. Представляет, однако, методический интерес вопрос о вычислении этих коэффициентов в квантовом случае; реально такой случай может представить гелий при достаточно низких температурах. Покажем, каким образом может быть вычислен второй вириальный коэффициент с учетом квантования парного взаимодействия частиц газа (Е. Beth, G. Е. Uhlenbeck, 1937). Мы будем рассматривать одноатомный газ, атомы которого не обладают электронным моментом; имея в виду случай гелия, будем для определенности считать также, что ядра атомов не имеют спина и что атомы подчиняются статистике Бозе.

В интересующем нас приближении достаточно сохранить в фор­муле (35,3), определяющей потенциал О, лишь первые три члена суммы по N:

Q«- Т InJ 1 +2^-^£i«^)/r ₊Ъ^-^Е*^пУТ\■ (77,1)

^х) Рассмотренному в конце § 74 случаю соответствует верхняя точка инвер­сии при Р—>-0(Т_хяв = 2а/Ь). Нижняя точка инверсии при малых Р в газе может отсутствовать ввиду его конденсации в жидкость.

Здесь Е_ы обозначают уровни энергии отдельного атома, a E_in — уровни энергии системы двух взаимодействующих атомов. Нашей целью является вычисление лишь тех поправочных членов в термо­динамических величинах, которые связаны с непосредственным

взаимодействием атомов; поправки же, связанные с квантовомеха-ническими обменными эффектами, имеющиеся уже в идеальном газе, определяются формулой (56,15), согласно которой обменная часть второго вириального коэффициента равна (в случае статис­тики Бозе)

В_о6м = -1-(лАутТГ'\ (77,2)

Таким образом, наша задача сводится к вычислению суммы

Z<*>=2exp(²-t^),

причем из нее должно еще быть вычтено выражение, которое получилось бы для двух невзаимодействующих атомов.

Уровни энергии Е_2п складываются из кинетической энергии движения центра инерции обоих атомов (р²/4т, где р—импульс этого движения, m—масса атома) и энергии их относительного движения. Последнюю мы обозначим через е; это есть уровни энергии частицы с массой т/2 (приведенная масса двух атомов), движущейся в центральном поле U₁₂ (г) (£/₁₃ — потенциальная энергия взаимодействия атомов). Движение центра инерции всегда квазиклассично, и, производя обычным образом интегрирование по его координатам и импульсам (ср. § 42), получим

_Z(2> ₌у_е2ц/т^£_у*^е~^е'^т.

Если обозначить посредством Z_B3 ту часть суммы Z⁽²>, которая связана со взаимодействием частиц, то можно написать Q в виде

Рассматривая второй член как малую добавку к первому и вы­ражая его через Т, V и N (с помощью формулы (45,5) для хими­ческого потенциала идеального газа), получим для свободной энергии выражение

Дифференцируя по V, получим давление, причем интересующая нас обусловленная взаимодействием атомов часть вириального коэффициента равна

Ввз(7') = -8(^)^3/Хз. (77,3)

Спектр уровней энергии е состоит из дискретного спектра отрицательных значений (соответствующих финитному относитель­ному движению атомов) и непрерывного спектра положительных значений (инфинитное движение). Первые обозначим посредст­вом е„; вторые же можно написать в виде р²/т, где р—импульс относительного движения атомов, разошедшихся на большое рас­стояние друг от друга. Сумма

2в^|Е«^,/г

п

по дискретному спектру входит в Z_B3 целиком. Из интеграла же по непрерывному спектру надо отделить часть, соответствующую свободному движению невзаимодействующих частиц. Для этого применим следующий прием.

На больших расстояниях г волновая функция стационарного состояния с орбитальным моментом / и положительной энер­гией р²/т имеет асимптотический вид

. const / р In. j. \

где фазы 8, = 6_г(/?) зависят от конкретного вида поля с7₁₂(г) (см. III, § 33). Положим формально, что область изменения рас­стояния г ограничена весьма большим, но конечным значением R. Тогда импульс р сможет принимать лишь дискретный ряд значе­ний, определяющихся граничным условием, требующим обраще­ния ij) в нуль при r = R:

■jrfl—-у + 6, = 5Я,

где s—целые числа. Но при большом R ряд этих значений очень густ, и в сумме

р

можно перейти к интегрированию. Для этого при заданном / умножаем суммируемое выражение на

и интегрируем по dp, после чего результат должен еще быть умножен на 21 +1 (кратность вырождения по направлениям орби­тального момента) и просуммирован по

2 е-р^т ₌ 1 ^ (21 + 1) | (| + fl) e-'W_dp. Для частиц, подчиняющихся статистике Бозе и не обладающих

спином, координатные волновые функции должны быть симметрич­ными; это значит, что допустимы лишь четные значения /, так что суммирование по / производится по всем четным числам.

При свободном движении все фазы 8_г = 0. Поэтому выраже­ние, остающееся при 6_г = 0, есть та часть суммы, которая должна быть отброшена как не связанная со взаимодействием атомов. Таким образом, получаем для искомого Z_B3 следующее выражение:

Z_B3= Ев^{1 е}" '^/r +12? (21 + 1) *$L_e-P^r_{dp> (77i4)}

п I о

а вириальный коэффициент fi = В_о6м + 5_ВЗ равен

В (Т) --1 (-^f-)'" (1 + 16Z_B3). (77,5)

Как известно фазы 8₍ определяют амплитуду рассеяния час­тиц, движущихся в поле U_]2(r), согласно формуле¹)

f (^Q) = wE^{21 +^{l) {е}™¹~^{1} р}< (^{cos е)}-i

где Р₁ — полиномы Лежандра, 6 — угол между направлениями падения и рассеяния; суммирование в данном случае произво­дится по всем четным значениям /. В связи с этим оказывается возможным выразить интеграл в (77,4) через амплитуду рассея­ния. Именно, легко проверить непосредственной подстановкой выражения для /(0) справедливость следующего соотношения:

Стоящая же слева сумма как раз входит в подынтегральное выра­жение в (77,4), и в результате его подстановки (и интегрирова­ния по частям в одном из членов) получим

оо

^Zb₃=Е ^е'⁸" ^1/Г + J P'e-p^r _[f(0)+ /* (0)]dp+

Если в поле (7₁₂ (г) имеются дискретные уровни, то при до­статочно низких температурах температурная зависимость В(Т) будет в основном определяться экспоненциально возрастающей

^х) См. III, § 123. Сечение рассеяния в элемент телесного угла do есть I/(9)|²do.

с уменьшением Т суммой по дискретным уровням. Дискретные уровни, однако, могут и отсутствовать вовсе; тогда вириальный коэффициент будет зависеть от температуры по степенному закону (если учесть, что при р—^0 амплитуда рассеяния стремится к постоянному пределу, то легко найти, что при достаточно низких температурах В будет определяться в основном чле­ном B_o6J.

Отметим, что в случае слабого взаимодействия, когда столкно­вения частиц могут быть описаны борцовским приближением, амплитуда рассеяния мала, и третий член в (77,6), квадратичный по этой амплитуде, может быть опущен. При слабом взаимодей­ствии отсутствуют связанные состояния, а потому отсутствует и первый член в (77,6). Используя известное выражение для амплитуды рассеяния /(0) в борновском приближении, пропор­циональное интегралу ^U₁₂r²dr, легко убедиться в том, что выражение для F в точности совпадает с формулой (32,3) (без квадратичного члена), как и должно было быть в этом случае.

Задача

В квазиклассическом случае определить квантовую поправку (порядка %²) в вириальном коэффициенте В (Г) одноатомного газа.

Решение. Поправка к классической свободной энергии дается формулой (33,15). Учитывая, что в данном случае осуществляется лишь парное взаимо­действие атомов и что U₁₂—функция только расстояния между атомами, найдем

_j^_'?(dU^y _e-u_lt/T_r4r ~ 6mT*){ dr J ^{6 f ar}-о

Это выражение представляет собой поправку к основному, классическому зна­чению, даваемому формулой (74,5). Отметим, что В_ив > 0.

§ 78. Термодинамические величины классической плазмы

Изложенный в § 75 метод вычисления термодинамических величин неидеального газа заведомо непригоден для газа, состо­ящего из заряженных частиц, взаимодействующих по закону Кулона, так как в этом случае входящие в формулы интегралы расходятся. Поэтому такой газ требует особого рассмотрения.

Рассмотрим полностью ионизованный газ (плазма). Заряды его частиц будем обозначать посредством z_ae, где индекс а отли­чает различные сорта ионов (е — элементарный заряд, z_a — поло­жительные и отрицательные целые числа). Пусть далее п_а0 есть число ионов а-го сорта в единице объема газа. Газ в целом, разумеется, электрически нейтрален, т. е.

%г_ап_а0 = 0. (78Д)

Будем считать, что газ слабо отклоняется от идеальности. Для этого во всяком случае необходимо, чтобы средняя энергия кулоновского взаимодействия двух ионов (~(ге)²/г, где r~n~¹/³— среднее расстояние между ионами) была мала по сравнению со средней кинетической энергией ионов (~Т). Таким образом, должно быть (ге)²п^г/³ *^.Т или

п<{^*У- (⁷⁸-2)

Ввиду электронейтральности плазмы среднее значение энергии кулоновского взаимодействия ее частиц, если бы все они были равномерно распределены в пространстве независимо друг от друга, обратилось бы в нуль. Поэтому первые поправки в тер­модинамических величинах плазмы (по сравнению с их значениями в идеальном газе) возникают только при учете корреляции между положениями различных частиц. С целью напоминать об этом обстоятельстве, будем называть эти поправки корреляционными.

Начнем с определения поправки в энергии плазмы. Как известно из электростатики, энергия электрического взаимодей­ствия системы заряженных частиц может быть написана в виде половины суммы произведений зарядов на потенциалы поля, соз­даваемого в точках их нахождения всеми остальными зарядами. В данном случае

£ко_РР = У- уЕздоФв. (78,3)

а

где ф_а — потенциал поля, действующего на ион а-го сорта со стороны остальных зарядов. Для вычисления этих потенциалов поступим следующим образом¹).

Каждый из ионов создает вокруг себя некоторое (в среднем сферически-симметричное) неравномерно заряженное ионное облако. Другими словами, если выбрать какой-либо из ионов в газе и рассматривать плотность распределения остальных ионов относи­тельно данного, то эта плотность будет зависеть только от рас­стояния г от центра. Обозначим плотность распределения ионов (а-го сорта) в этом ионном облаке посредством п_а. Потенциальная энергия каждого иона а-го сорта в электрическом поле вокруг данного иона есть г_аец>, где ср — потенциал этого поля. Поэтому, согласно формуле Больцмана (38,6), имеем

rt_a = tt_o0exp(-i^). (78,4)

^J) Излагаемый метод был применен Дебаем и Хюккелем для вычисления термодинамических величин сильных электролитов (P. Debye, Е. Htickel, 1923).

Постоянный коэффициент положен равным п_аВ, так как вдали от центра (где <р —»- 0) плотность ионного облака должна переходить в среднюю ионную плотность в газе.

Потенциал ср поля в ионном облаке связан с плотностью заря­дов в нем (равной 2^е2Л) электростатическим уравнением Пу­ассона

Д_ф== — 4я<?2 z_an_a. (78,5)

а

Формулы (78,4—5) составляют вместе систему уравнений само­согласованного электрического поля электронов и ионов.

При сделанном нами предположении об относительной сла­бости взаимодействия ионов энергия ег_ац> мала по сравнению с Т, и формулу (78,4) можно написать приближенно в виде

"_а = "аО-^ф. (78,6)

Подставив это выражение в (78,5) и имея в виду условие (78,1) нейтральности газа в целом, получим уравнение

Аф — х²ф = 0, (78,7)

где введено обозначение

*² = ^Ц«ао^.' (78,8)

а

Величина и имеет размерность обратной длины.

Центрально-симметричное решение уравнения (78,7) есть

е~"^лг

Ф = const —.

В непосредственной близости от центра поле должно переходить в чисто кулоновское поле данного заряда (величину которого обозначим как z_be). Другими словами, при достаточно малых г должно быть ужег_ь/г\ поэтому надо положить const—z_be, так что искомое распределение потенциала дается формулой

„ _{Ф = е2б}-^1. (78,9)

Отсюда видно, кстати, что поле становится очень малым на рас­стояниях, больших по сравнению с 1/и. Поэтому длину 1/к можно рассматривать как определяющую размеры ионного облака, созда­ваемого данным ионом (ее называют также дебаевским радиусом). Все производимые здесь вычисления, конечно, предполагают, что этот радиус велик по сравнению со средними расстояниями между ионами (это условие совпадает, очевидно, с условием (78,2)).

Разлагая потенциал (78,9) в ряд при малых кг, найдем Ф = ^—ez_bn+...

Опущенные члены обращаются при г = 0 в нуль. Первый член есть кулоново поле самого данного иона. Второй же член есть, очевидно, потенциал, создаваемый всеми остальными ионами облака в точке нахождения данного иона; это и есть та величина, которая должна быть подставлена в формулу (78,3): ср_в = — ег_ак.

Таким образом, мы получаем следующее выражение для кор­реляционной части энергии плазмы:

£_Ko_PP = -Y^²E^rtao^ = -Ve³ Yt(Е^У", (78,10)

а \ а /

или, вводя полные числа различных ионов в газе N_a — n_a0V:

£корр=-^е - У w (Е ад)^8/а. (78,11)

Эта энергия обратно пропорциональна квадратному корню из температуры и из объема газа.

Е д F

Интегрируя термодинамическое соотношение — —-gf f >

можно найти из Е_кою соответствующую добавку к свободной
энергии:

F = F*-²4 Уw(E«)^3/2 (⁷М2)

(постоянную интегрирования надо положить равной нулю, так как при Т—>-оо должно быть F — F_m). Отсюда давление

NT _____ е>_

V зуз/а

j/'ffE^y⁷³ - (78,13)

где N = ^N_a. Термодинамический потенциал Ф можно получить из F с помощью теоремы о малых добавках (как это было сде­лано и в § 74), т.е. рассматривая второй член в (78,12) как малую добавку к F_sli и выразив ее с нужной точностью через переменные Р и Г¹):

*) Для перехода от (78,11) к (78,12) такой способ не мог быть применен, поскольку энергия (78,11) не была выражена через необходимые для этого переменные S и V.

^ф=^ф_ад-ж(^)^1/8(Е«)^4/а- <⁷⁸>¹⁴>

§ 79. Метод корреляционных функций

Преимущество изложенного в предыдущем параграфе метода Дебая — Хюккеля состоит в его простоте и физической прозрач­ности. С другой стороны, его основной недостаток заключается в невозможности обобщения для вычисления следующих прибли­жений по концентрации. Мы изложим поэтому вкратце также и другой метод (предложенный Н. Н. Боголюбовым, 1946), хотя и более сложный, но позволяющий в принципе вычислить также и следующие члены разложения термодинамических величин.

Этот метод основан на рассмотрении так называемых корре­ляционных функций между одновременными положениями несколь­ких частиц в заданных точках пространства. Простейшей и наи­более важной из них является бинарная корреляционная функция w_ab, пропорциональная вероятности найти одновременно две частицы (иона) в заданных точках х_а и х_ь (оба иона а и Ь могут быть как одного, так и разных родов). Ввиду изотропии и одно­родности газа эта функция зависит, конечно, лишь от г = |т_ь — г_а\. Мы выберем нормировочный коэффициент в функции w_ab таким образом, чтобы она стремилась к единице при г—>-оо.

Если функция w_ab известна, искомая энергия Е_К09Р может быть найдена путем интегрирования по очевидной формуле¹)

£к_0Рр = £ N_aN_b j j u_abw_abdV_adV_b, (79,1)

a, b

где суммирование ведется по всем родам ионов, а и_аЬ — энергия кулоновского взаимодействия пары ионов на расстоянии г.

Согласно формуле распределения Гиббса функция w_ab дается следующим выражением:

™_ab = yj^rr J ехр { ^F-^F^-^U } dV.dV,... dV_N-_t, (79,2)

где U — энергия кулоновского взаимодействия всех ионов, а ин­тегрирование производится по координатам всех ионов, за исклю­чением двух данных ионов. Для приближенного вычисления этого интеграла воспользуемся следующим приемом.

Дифференцируем равенство (79,2) по координатам иона Ь:

¹) Сама по себе эта формула не связана, конечно, с кулоновским характе­ром взаимодействия частиц и предполагает лишь его парность.

^dwab ^wab ди_аЬ 1_VW Г ^диЬс „■ лу (-JQ Q\

в результате чего система сводится к одному уравнению

Дсо (г) — и²со (г) = ^ б (г). (79,8)

Это окончательное уравнение имеет ту же форму, что и уравнение (78,7) в методе Дебая — Хюккеля (член с б-функцией в (79,8) соответствует граничному условию при г—у 0, наклады­ваемому на функцию ср (г) в (78,7)). Решение уравнения (79,8):

чем и определяются бинарные корреляционные функции в плазме.

Для вычисления энергии достаточно подставить теперь w_ab из (79,4), (79,7), (79,9) в (79,1). Переходя к интегрированию по относительным координатам двух частиц, находим

Якорр = -1 £ п_ап„ J. - " 4яг* dr

а, Ь О

(член 1 в w_ab не дает вклада в энергию в силу условия электри­ческой нейтральности плазмы). Произведя интегрирование, вер­немся к прежнему результату (78,11).

В следующем приближении вычисления становятся более гро­моздкими. В частности, предположение (79,5) теперь недостаточно, и следует ввести тройные корреляции, не сводящиеся уже к би­нарным. Для них получается уравнение, аналогичное (79,3), со­держащее теперь четверные корреляции, которые, однако, в дан­ном (втором) приближении сводятся к тройным¹).

§ 80. Термодинамические величины вырожденной плазмы

В изложенной в § 78 теории предполагалось, что плазма далека от вырождения, т. е. подчиняется статистике Больцмана. Рассмотрим теперь ситуацию, когда температура плазмы настолько низка, что ее электронная компонента уже вырождена:

_аГ<^./1»/«, (80,1)

где т—масса электрона (ср. (57,8)); при этом ионная компонента благодаря большой массе ионов может быть еще далека от вырож-

^х) Члены следующего порядка в термодинамических величинах плазмы фактически вычислены (другим методом) А. А. Веденоеым и А. И. Ларкиным, ЖЭТФ 36, 1133 (1959).

дения. Напомним, что условие слабой неидеальности вырожден­ной плазмы состоит в требовании

mz^2/3e² Рп^1/3

<1 (80,2)

(см. (57,9)); оно выполняется тем лучше, чем выше плотность плазмы.

Для вырожденного газа удобными переменными являются (помимо температуры Т и объема V) его химические потенциалы р₀ вместо чисел частиц М_а¹). Соответственно этому будем вычи­слять Q—термодинамический потенциал по отношению к этим переменным. Отметим, что химические потенциалы не являются при этом все независимыми переменными; они связаны друг с другом одним соотношением, следующим из условия электри­ческой нейтральности плазмы:

а а

Воспользуемся формулой

/еа \ —(ёИ\

выражающей производную от Q по некоторому параметру к через среднее значение такой же производной от гамильтониана системы (ср. аналогичные формулы (11,4), (15,11)). В данном случае выберем в качестве параметра X квадрат заряда е². Гамильтониан плазмы содержит е² в виде общего коэффициента в операторе кулонов­ского взаимодействия частиц 0. Поэтому

Дата добавления: 2014-11-07