Ol — V2X 18 страница

Минимальная работа будет затрачена, если процесс происхо­дит обратимо. Произведенная внешним источником работа равна при этом изменению энергии системы, т. е.

8R_mia = 8E + bE₀

(величины без индекса относятся к данной малой части, а с ин­дексом нуль—к остальной системе). Заменим б£₀ его выражением через изменения независимых переменных:

8R_min=bE + T₀8S₀—P₀8 V₀ + pi Sfl₀,

где р₀—химический потенциал растворенного вещества в среде; число частиц растворителя при рассматриваемом процессе не изме­няется, и поэтому аналогичного члена для растворителя писать не нужно¹). Из обратимости процесса следует, что 6S„=—6S, а из сохранения полного объема и количества растворенного веще­ства для всего раствора имеем: 6V=—bV_a, бя =—8п₀. Под­ставляя это, находим окончательное выражение для искомой работы

6i?_min = 6£-r₀6S + P₀6F-p₀6n. (96,1)

Таким образом, в качестве условия равновесия мы можем потре­бовать для любой малой части раствора выполнения неравенства

б£—T₀8S + P₀8V—р'₀6п>0. (96,2)

Ниже мы будем, как и в § 21, опускать индекс нуль у выра­жений, стоящих в качестве коэффициентов при отклонениях вели­чин от их равновесных значений; всегда будут подразумеваться значения этих выражений в состоянии равновесия.

Разл'ожим 8Е в ряд по степеням 8V, 8S и бп (рассматривая Е как функцию от V, S и п). С точностью до членов второго порядка

¹) Дифференциал энергии для среды (при постоянном N): dE₀ = Т₀ dS₀ —Р₀ dV₀ + ц'о dn₀. Поскольку величины Г₀, Р₀, Но можно считать постоянными, то интегриро­вание этого равенства даст такое же соотношение между конечными измене­ниями величин Е₀, S₀, V_a, п₀. Не смешивать р:о с химическим потенциалом чистого растворяемого ве­щества!

^8Е = -I"⁶⁵ + § ^бУ + Ж ^б" + Т [ W ^№ + IS" № + S-^б»² +

Но

дЕ

dV

дЕ

dS

дЕ

Поэтому при подстановке в (96,2) члены первого порядка сокра­тятся, и мы получим

Из теории квадратичных форм известно, что для того, чтобы форма с тремя переменными (в данном случае—6S, 8V, 6га) была всегда положительна, ее коэффициенты должны удовлетворять трем условиям, которые для формы (96,3) имеют вид

д^2Е	д^2Е	д^2Е
dV^2	dVdS	dVdn
д^2Е	д^2Е	д^2Е
dSdV	dS^2	dSdn
д^2Е	д^2Е	д^2Е
dndV	дп dS	дп^2

>о,

д²Е dV² д²Е

dSdV

д²Е

dV dS

д²Е

dS²

> 0, -g- > 0. (96,4)

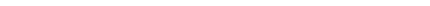
(96,5)

Эти определители представляют собой якобианы

w-^T-^) _<0 (^д(^р>^ТЛ _<0 (*L) >₀

Второе и третье из этих условий дают уже известные нам неравенства (dP/dV)_Tt „ < 0 и C_v > 0. Что касается первого, то его можно преобразовать следующим образом:

а(Р, т, |х') (дц'\

<0.

'д (V, S)

д(Р, Т, р,') _ д(Р, Т, п) _ \ дп)р, т d(V, S, п) ~ д (V, S, п) ~~ д(Р, Т,п)

\д (Р, Г),

Поскольку согласно второму из условий (96,5) знаменатель здесь отрицателен, должно быть

(ж)р,г>°- <^%'⁶>

от 0 до 1). Состояние бинарной смеси можно изобразить точкой в трехмерной системе координат, на осях которой откладываются значения этих трех величин (аналогично тому, как состояние системы из одинаковых частиц мы изображали точкой на пло­скости Р, Т).

Система из двух компонент может состоять, согласно правилу фаз, не больше чем из четырех соприкасающихся фаз. При этом число степеней свободы такой системы равно двум для двух фаз, одному для трех фаз и нулю—для четырех. Поэтому состояния, в которых находятся в равновесии друг с другом две фазы, изображаются точками, образующими поверхность в трехмерной системе координат; состояния с тремя фазами (тройные точки) — точками на линии (называемой линией тройных точек или трех­фазной линией), а состояния с четырьмя фазами—изолирован­ными точками.

Напомним (§ 81), что в случае систем с одной компонентой состояния, в которых находятся в равновесии две фазы, изобра­жаются кривой на диаграмме Р, Т; каждая точка этой кривой определяет давление и температуру обеих фаз (которые одина­ковы в обеих фазах согласно условиям равновесия). Точки же, лежащие по сторонам кривой, представляют однородные состоя­ния тела. Если же на осях координат откладывать температуру и объем, то равновесие фаз изображается кривой, точки внутри которой представляют собой состояния, в которых происходит расслоение на две фазы, изображающиеся точками пересечения прямой Т — const с кривой равновесия.

Аналогичное положение вещей имеет место для смесей. Если на осях координат откладывать значения Р, Т и химического потенциала одной из компонент (т. е. величин, имеющих одинако­вое значение в соприкасающихся фазах), то равновесие двух фаз изобразится поверхностью, каждая точка которой определяет Р, Т, р для обеих находящихся в равновесии фаз. В случае нали­чия трех фаз точки, изображающие их равновесие (тройные точки), будут лежать на кривых пересечения поверхностей равновесия каждых двух из них.

Однако пользование переменными Р, Т, р неудобно, и мы будем употреблять в дальнейшем в качестве независимых пере­менных величины Р, Т, х. В этих переменных равновесие двух фаз изображается поверхностью, точки пересечения которой с прямой Р = const, Т — const изображают состояния обеих соприкасаю­щихся фаз при данных Р и Т (т. е. определяют их концентрации, которые, конечно, могут быть различны в обеих фазах). Точки, лежащие на этой прямой между двумя точками пересечения, являются состояниями, в которых однородное тело неустойчиво и где поэтому происходит расслоение на две фазы (изображаю­щиеся точками пересечения).

Ниже мы будем обычно изображать двумерные диаграммы, откладывая на осях координат Р и х или Т и х; в таких коор­динатах можно чертить линии пересечения поверхности равнове­сия с плоскостями постоянной температуры или давления. Эти линии будем называть кривыми равновесия.

Рассмотрим точки кривой равновесия, в которых концентрации в обеих фазах становятся одинаковыми. При этом возможны два случая: 1) в такой точке также и все остальные свойства обеих фаз делаются одинаковыми, т. е. обе фазы становятся тождест­венными; 2) в такой точке продолжают существовать две различ­ные фазы. В первом случае точка называется критической, а во втором будем называть ее точкой равных концентраций.

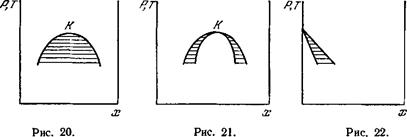
Вблизи критической точки кривая равновесия имеет вид, изображенный на рис. 20 или аналогичный, при котором крити­ческая точка К является точкой минимума (на оси абсцисс откла­дывается х, а на оси ординат—Р или Т; кривая является тогда пересечением поверхности равновесия с плоскостями соответст­венно постоянной температуры или постоянного давления). Точки, лежащие внутри этой кривой (в заштрихованной области), пред­ставляют собой область состояний, в которых происходит рас­слоение на две фазы; концентрации в этих фазах определяются точками пересечения кривой с соответствующей горизонтальной прямой. В точке К обе фазы сливаются. Между любыми двумя точками в незаштрихованной области можно совершить непрерыв­ный переход по любому пути, обходящему критическую точку.

Как видно из рис. 20, вблизи критической точки существуют состояния, в которых находятся друг с другом в равновесии две фазы со сколь угодно близкими концентрациями х и х + Ьх. Для таких фаз условие равновесия имеет вид

ц(Р, Т, х) = ц(Р, Т, х + вх),

где р.—химический потенциал одного из веществ в смеси. Отсюда видно (ср. § 83), что в критической точке должно выполняться

условие

(97,1)

Это условие тождественно с условием (96,8); поэтому оба опре­деления критической точки (здесь и в § 96) эквивалентны. Заме­тим, что в (97,1) под ц подразумевается химический потенциал любого из двух веществ в смеси. Однако оба условия, которые получаются, если взять в (97,1) один или другой химический потенциал, в действительности эквивалентны, в чем легко убе­диться, если заметить, что каждый из химических потенциалов есть производная от Ф по соответствующему числу частиц, а Ф есть однородная функция первого порядка от обоих чисел частиц.

Критические точки, очевидно, образуют некоторую линию на поверхности равновесия.

Вблизи точки равных концентраций кривые равновесия должны иметь вид, изображенный на рис. 21 (или аналогичный, где точка равных концентраций К есть точка минимума). Обе кривые касаются в точке максимума (или минимума). Область между обеими кривыми представляет собой область разделения на фазы. В точке К концентрации обеих фаз, находящихся в равновесии друг с другом, делаются одинаковыми, однако фазы продолжают существовать как различные. Действительно, перейти от одной из совпадающих в К точек к другой можно только пересекая область разделения на две фазы. Как и критические точки, точки равных концентраций лежат на некоторой кривой на поверхности равновесия.

Рассмотрим теперь свойства кривых равновесия при малых концентрациях (т. е. когда одного из веществ в смеси значи­тельно меньше другого; х близко к нулю или к единице).

В § 89 было показано, что при малых концентрациях (слабые растворы) разность между температурами равновесия фаз раство­ров и чистого вещества (при одном и том же давлении) пропор­циональна разности концентраций обеих фаз. То же относится к разности давлений при одной и той же температуре. Кроме того, в § 90 было показано (опять-таки для малых концентраций), что отношение концентраций в обеих фазах зависит только от Р и Т, и потому в области вблизи х = 0 это отношение можно считать величиной постоянной.

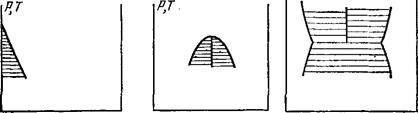
Из всего этого следует, что при малых концентрациях кри­вые равновесия имеют вид, изображенный на рис. 22, т. е. состоят из двух пересекающихся на оси ординат прямых (или аналогичный, где прямые направлены вверх). Область между обеими прямыми есть область разделения на фазы. Области над и под обеими прямыми являются областями одной и дру­гой фаз.

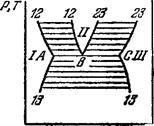
В начале этого параграфа уже указывалось, что система с двумя компонентами может состоять из трех соприкасающихся фаз. Вблизи тройной точки кривые равновесия выглядят так, как изображено на рис. 23. Все три фазы имеют при равновесии одинаковые давление и температуру. Поэтому точки А, В, С, определяющие их концентрации, лежат на одной прямой, парал­лельной оси абсцисс. Точка А, определяющая концентрацию первой фазы в тройной точке, есть точки пересечения кривых 12 и 13 равновесия первой фазы со второй и первой с третьей. Аналогично точки В и С являются пересечениями кривых 12 и

23 равновесия первой фазы со второй
и второй с третьей (точка В) и кривых
23 и 13 равновесия второй фазы с
третьей и первой с третьей (точка С).
Точки А, В, С являются, конечно, точ-
ками пересечения плоскости Р = const
или 7" = const с тремя линиями на по-
верхности равновесия; из этих линий
мы будем называть линией тройных
^ точек или трехфазной линией ту, кото-
Рис. 23. рая соответствует точке В. Области
/, // и /// представляют собой со-
стояния отдельных фаз: первой, второй и третьей. Область между
обеими кривыми 13 под прямой ABC есть область разделения
на первую и третью фазы, а область между обеими кривыми 12
и обеими кривыми 23 (над ABC) соответственно на первую и
вторую и вторую и третью фазы. Область // должна, очевидно,
быть расположена целиком над ABC (или целиком под ABC).
В точках А, В и С кривые 12, 13 и 23 пересекаются, вообще
говоря, под- некоторыми углами, а не переходят друг в друга
непрерывным образом. Направления кривых 12, 13, 23, конечно,
не обязательно должны быть такими, как изображено на рис. 23.
Существенно только, что кривые 12 и 23 и кривые 13 должны
лежать по разные стороны от прямой ABC.

Если спроецировать какую-нибудь из рассмотренных особых линий поверхности равновесия на плоскость Р, Т, то такая проек­ция разделит эту плоскость на две части. В случае критической линии на одну из этих частей спроецируются точки, соответст­вующие двум различным фазам, и точки, соответствующие раз­делению на эти две фазы. На другую же часть плоскости Р, Т спроецируются точки, изображающие однородные состояния, причем ни в одной из них не происходит разделения на две фазы. На рис. 24 пунктирная линия изображает проекцию кри­тической линии на плоскость Р, Т. Буквы а и Ь обозначают две фазы. Символ а—Ь означает, что на эту часть плоскости проеци­руются состояния двух фаз и состояния, где эти две фазы нахо­дятся в равновесии друг с другом. Символ ab означает одну фазу, в которую сливаются фазы а и Ь выше критических точек.

Аналогично проекция трехфазной линии тоже делит плоскость Р, Т на две части. Рис. 25 показывает, какие точки проеци­руются на эти части. Символ а—b—с означает, что сюда проеци­руются точки, изображающие состояния фаз а, Ь, с и состояния, в которых происходит расслоение на фазы а и Ь или Ъ и с.

тк П ™

ab

а-Ь-с

а-д-с

Рис. 24.

Рис. 25.

Рис. 26.

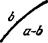
Рис. 26 изображает такую же проекцию для линии точек равных концентраций, а рис. 27—линии равновесия фаз чистого вещества (т. е. точек х~0 или х = 1); последняя, очевидно, сама лежит на плоскости Р, Т. Буква b на рис. 27 означает, что на эту часть плоскости проецируются точки, со- j-ответствующие состояниям только фазы Ь. Мы условимся в последовательности букв в символах а—b, а—b—с буквой b обозна­чать фазу с большей концентрацией, чем а, и буквой с—фазу с большей концентрацией, чем Ь¹).

Отметим, что четыре типа особых точек
кривых равновесия (тройная точка, точка
равных концентраций, критическая и точка Рис. 27.

чистого вещества) представляют собой четыре возможных типа максимумов (или минимумов) этих кривых.

Если какая-нибудь из фаз имеет всегда (т. е. независимо от значений Р и Т) один и тот же определенный состав, то кривые равновесия вблизи рассмотренных нами точек несколько упро­щаются. Такие фазы представляют собой химическое соединение обеих компонент или же являются фазами чистого вещества, т. е. фазами, имеющими всегда концентрацию х = 0 (или х=1).

Рассмотрим вид кривых равновесия при наличии фаз постоян­ного состава вблизи точек, в которых линии, соответствующие

*) Подчеркнем во избежание недоразумений, что обозначение а—Ь—с в случае линии равных концентраций (в отличие от случая трехфазной линии) имеет в известном смысле условный характер: буквы а и с обозначают здесь состояния, по существу не являющиеся двумя различными фазами, так как они никогда не существуют одновременно, соприкасаясь друг с другом.

этим фазам, оканчиваются. Очевидно, что такие точки должны быть точками максимума или минимума кривых равновесия, а потому относятся к рассмотренным в этом параграфе типам точек.

Если фаза постоянного состава является фазой чистого веще­ства с концентрацией л:=0, то соответствующая ей линия сов­падает с осью Р или Т и может окончиться в точке типа, изо­браженного на рис. 28. На этом рисунке изображен вид кривой равновесия вблизи такой точки; одна из прямых рис. 22 сливается с осью ординат.

PJ

ге сс сс

Рис. 28. Рис. 29. Рис. 30.

Если одна из фаз представляет собой химическое соединение определенного состава, то вблизи точки равных концентраций кривая равновесия приобретает вид, изображенный на рис. 29, т. е. внутренняя область на рис. 21 превращается в вертикаль­ную прямую. Заштрихованная область по обе стороны ее является областью разделения на фазы, одна из которых — химическое соединение, состав которого определяется этой прямой. В точке максимума кривая не имеет (как и на рис. 21) излома.

Аналогично, вблизи тройной точки кривые равновесия приоб­ретают вид, показанный на рис. 30. Фаза, являющаяся химиче­ским соединением, изображается вертикальной линией, к которой сводится в этом случае область // на рис. 23.

§ 98. Примеры диаграмм состояния

В этом параграфе мы перечислим основные типы кривых равно­весия; в отличие от предыдущего параграфа мы будем рассмат­ривать теперь их вид не только вблизи особых точек, но и цели­ком. Эти кривые (называемые также диаграммами состояния) могут иметь весьма разнообразную форму, в большинстве же случаев, однако, она подходит под один из приведенных ниже типов, или же является комбинацией нескольких из них. Заштри­хованные области на всех этих диаграммах всегда являются областями разделения на фазы, а незаштрихованные—областями

однородных состояний. Точки пересечения горизонтальных линий с кривыми, ограничивающими области разделения на фазы, опре­деляют состав фаз, на которые (при данных Р и Т) происходит разделение. Относительные количества обеих фаз определяются при этом тем же «правилом рычага», о котором упоминалось в §81.

Ниже мы говорим для определенности о диаграммах Т, х; такие же типы диаграмм возможны и в координатах Р, х. Кон­центрация х откладывается вдоль оси абсцисс и меняется в преде­лах от 0 до 1.

1. Имеются две фазы; каждая из них может обладать любой концентрацией (т. е. обе компоненты в обеих фазах смешиваются в произвольных отношениях). В простейшем случае, когда кривые не имеют никаких максимумов или jr минимумов (кроме точек чистого ве­щества), диаграмма состояния имеет вид, изображенный на рис: 31 (так называемая сигара).

я.

Пусть одной из фаз является жидкость (область под сигарой), а другой—пар (область над сигарой); F верхняя кривая сигары называется в этом случае кривой конденсации, а нижняя — кривой точек кипения¹).

Если нагревать жидкую смесь определенного состава, то при тем­пературе, определяющейся пересечением вертикальной прямой AD (соответствующей данной концентрации) с нижней кривой сигары (точка В), жидкость начнет кипеть. При этом выкипает пар, состав которого определяется точкой С, т. е. обладает мень­шей концентрацией, чем жидкость. Концентрация остающейся жидкости будет, очевидно, повышаться, а соответственно будет повышаться ее точка кипения. При дальнейшем нагревании точка, изображающая состояние жидкой фазы, будет передвигаться вверх по нижней кривой, а точка, изображающая выкипающий пар,— вверх по верхней кривой. Кипение закончится при различных температурах в зависимости от того, каким образом происходит процесс. Если кипение происходит в закрытом сосуде, так что весь выкипающий пар остается все время в соприкосновении с жидкостью, то, очевидно, жидкость целиком выкипит при тем­пературе, при которой пар имеет концентрацию, равную перво­начальной концентрации жидкости (точка D). Таким образом, в этом случае начало и конец кипения происходят при темпера­турах, определяемых пересечением вертикальной прямой AD

^г) Закономерности кипения и конденсации жидких смесей были установлены Д. П. Коноваловым (1884).

с нижней и с верхней кривой сигары. Если же выкипающий пар все время удаляется (кипение в открытом сосуде), то в равновесии с жидкостью в каждый момент находится лишь только что вы­кипевший пар. Очевидно, что в этом случае кипение закончится в точке G кипения чистого вещества, в которой состав жидкости и пара одинаков. Подобным же образом происходит конденсация пара в жидкость.

Совершенно аналогичное положение имеет место в случае, когда двумя фазами являются жидкость (область над сигарой), и твердое тело (область под сигарой).

я ее сп

Рис. 32. Рис. 33. Рис. 34.

2. Обе компоненты смешиваются в обеих фазах в произвольных
отношениях (как и в предыдущем случае), но имеется точка равных
концентраций. При этом диаграмма состояния имеет вид, изобра-
женный на рис. 32 (или аналогичный с минимумом). В точке
равных концентраций обе кривые имеют максимум или минимум
и касаются друг друга.

Переход из одной фазы в другую происходит подобно тому, как было описано в предыдущем случае, с той лишь разницей, что процесс может закончиться (если одна из фаз все время уда­ляется— например, при кипении жидкости в открытом сосуде) не только в точке чистого вещества, но и в точке равных кон­центраций. При составе, соответствующем самой этой точке, переход совершается целиком при одной температуре¹).

3. Имеются две фазы—жидкость и газ, в которых обе ком-
поненты произвольно смешиваются, причем имеется критическая
точка. Диаграмма состояния изображена на рис. 33 (К—крити-
ческая точка). Область справа от кривой соответствует жидким
состояниям, а область слева — газообразным. Следует, однако,
помнить, что при наличии критической точки можно, строго говоря,

Смесь, соответствующую точке равных концентраций, называют также азеотропной.

различать жидкую и газообразную фазы лишь тогда, когда обе находятся одновременно в равновесии друг с другом.

Диаграмма рассматриваемого типа приводит к следующему свое­образному явлению. Если нагревать в закрытом сосуде жидкость, состав которой изображается прямой АС (проходящей справа от точки К), то после начала кипения (в точке В) по мере даль­нейшего нагревания количество пара будет постепенно возрастать, но, начиная с некоторого момента, начнет снова уменьшаться, пока пар не исчезнет вовсе в точке С (так называемая ретро­градная конденсация).

4. Две жидкости смешиваются не во всех отношениях. Диа­грамма состояния изображена на рис. 34. При температурах выше температуры критической точки К компоненты смешиваются в произвольных отношениях. Ниже этой температуры компоненты не смешиваются в тех отношениях, которые изображаются точками внутри заштрихованной области. В этой области происходит расслоение на две жидкие смеси, концентрации которых опреде­ляются точками пересечения соответствующей горизонтальной прямой с кривой равновесия. Возможны аналогичные диаграммы, где точка К является точкой минимума, а также такие, где имеются две критические точки: верхняя и нижняя, так что область расслоения на две фазы (два раствора) ограничена замк­нутой кривой.

5. В жидком (или газообразном) состоянии обе компоненты смешиваются в произвольных отношениях. В твердом же (или жидком)—не во всех отношениях (ограниченная смешиваемость). В этом случае существует тройная точка. Смотря по тому, лежит ли температура тройной точки ниже температур равновесия фаз чистых компонент (точки Л и С) или между ними (она не может, очевидно, лежать выше них при сделанном нами предположении, что в более высокой фазе компоненты произвольно смешиваются), диаграммы состояния имеют такой вид, как изображено соответ­ственно на рис. 35 и 36. Пусть, например, фаза с неограничен­ной смешиваемостью является -жидкостью, а с ограниченной смешиваемостью—твердым телом. Область над кривой ABC (рис. 35) или ADC (рис. 36) есть область жидких состояний; области по сторонам от ADF и CEG (рис. 35) или ABF и CEG (рис. 36)—области однородных твердых фаз (твердых растворов). В тройной точке (температура которой определяется прямой DBE) находятся в равновесии жидкость и два твердых раствора с раз­ными концентрациями. Точка В на рис. 35 называется эвтекти­ческой точкой. Жидкая смесь, обладающая концентрацией, соот­ветствующей этой точке, замерзает целиком при этой же кон­центрации (в то время как при других концентрациях вымерзает твердая смесь с концентрацией, отличной от концентрации жидкости). Области ADB и СБЕ (рис. 35) и области ADB и

GDE (рис. 36) соответствуют разделению на жидкую и одну из твердых фаз; области DEGF (рис. 35) и BEGF (рис. 36)—раз­делению на две твердые фазы.

Если в случае диаграммы типа рис. 35 в твердом состоянии компоненты совсем не смешиваются, то диаграмма состояния приобретает вид, изображенный на рис. 37. В заштрихованных областях выше прямой АБС находятся в равновесии смешанная жидкая фаза с твердой фазой одного из чистых веществ, а под АБС—твердые фазы обоих чистых веществ. При понижении температуры жидкой смеси из нее вымерзает одно или другое

F G х Г G х ос

Рис. 35. Рис. 36. Рис. 37.

чистое вещество, смотря по тому, лежит ли концентрация жид­кости справа или слева от эвтектической точки. По мере даль­нейшего понижения температуры состав жидкости изменяется по кривой DB или ЕВ, и жидкость замерзает целиком в эвтекти­ческой точке В.

6. В жидком состоянии обе компоненты смешиваются в про­извольных отношениях. В твердом же состоянии компоненты не смешиваются вовсе, но образуют химическое соединение опреде­ленного состава. Диаграмма состояния изображена на рис. 38. Прямая DE определяет состав химического соединения. Имеются две тройные точки В и G, в которых находятся в равновесии жидкая фаза, твердое химическое соединение и твердая фаза одной из чистых компонент. Между точками В и G находится точка равных концентраций D (ср. рис. 29). Легко видеть, где и на какие фазы происходит разделение: в области DBE—на жидкую фазу и твердое химическое соединение, под прямой СБЕ—на химическое соединение и одно из твердых чистых ве­ществ, и т. д. Замерзание жидкости оканчивается в одной из эвтектических точек G или В, смотря по тому, лежит ли кон­центрация жидкости справа или слева от прямой DE.

7. В жидком состоянии обе компоненты смешиваются в про­извольных отношениях, а в твердом не смешиваются вовсе, но образуют химическое соединение, разлагающееся, однако, при

некоторой температуре — раньше, чем наступит плавление. Прямая, определяющая состав этого соединения, не может окончиться, как в предыдущем случае, в точке равных концентраций, так как не доходит до точки плавления. Поэтому она может окончиться в тройной точке типа, изображенного на рис. 30 в § 97 (точка А на рис. 39). На рис. 39, изображающем возможный вид диаграммы состояния для этого случая, легко видеть, на какие фазы про­исходит разделение в различных точках заштрихованной области.

8. В твердом состоянии компоненты вовсе не смешиваются, а в жидком — не во всех отношениях. В этом случае имеются две тройные точки, в которых находятся в равновесии жидкость

с двумя твердыми чистыми веществами (точка В на рис. 40) и одно из чистых веществ с двумя смешанными жидкими фазами различных концентраций (точка D). Незаштрихованные области над ABC и над DE изображают жидкие состояния с различными концентрациями; заштрихованная область над CD — область раз­деления на две жидкие фазы; область DEF — разделение на жид­кость и одно из чистых твердых веществ, и т. д.

Дата добавления: 2014-11-07