Ol — V2X 17 страница

Ho^Tlncoi-f-ifri+CoiPii.

ро₂ = Г lnc₀₂-f TJ?₂-(-c₀₂R22,

где pot, рог—химические потенциалы чистых растворяемых веществ. Совмест­ные же растворимости с'_п, с'о₂ определяются условиями

Poi = 7'lncoi + i|)₁+CoiP₁₁+Co₂p_i2,

\io₂ = T 1псо₂-г"ф₂ + ^со₂Р₂₂ + С|)]Р₁₂.

Вычитая (1) почленно из (2) и имея в виду относительную малость изменений растворимостей (бс₀₁ =coi—с₀₁<^с₀₁, 8с₀₂<^с₀₂), находим

Т ——=—с₀₂р₁₂, Т——- = — c_0lPi₂.

••01 ^с02

Отсюда

т. е. изменения растворимостей обоих веществ одинаковы.

3. Найти связь между изменениями давления насыщенных паров двух рас­творенных веществ в присутствии друг друга.

Решение. Давления насыщенных паров над растворами каждого из ве­ществ в отдельности определяются условиями равновесия

Т InPi + Xi (Т) = Т InCi + ^+CjPn, Т In Р₂ + х₂ (Г) = Г In с₂ +1₂+с₂р₂₂ (выражения слева — химические потенциалы обоих веществ в паре). Давления же Р\ и Р₂ над совместным раствором — из условий

Т In р[ + xi = Т In d + ifc + _Clp_u+c₂p₁₂, Г In P₂+Xs = Г Ь c₂ + ^₂ + c₂p₂₂ + _Clp„. Отсюда для малых изменений 6Р₁ = Р[—P_lt SP₂ находим

Т -p^-=c₂Pi2, Т -р^-=с₁р₁₂,

и затем искомое соотношение

№_t.8P, с,

§ 91. Выделение тепла и изменение объема при растворении

Процесс растворения сопровождается выделением или погло­щением тепла; мы займемся теперь вычислением этого теплового эффекта. Предварительно определим максимальную работу, кото­рая может быть совершена за счет процесса растворения.

Предположим, что процесс растворения производится при постоянных давлении и температуре. В таком случае максималь­ная работа определяется изменением термодинамического потен­циала. Вычислим ее для процесса, при котором в растворе кон­центрации с растворяется еще некоторое небольшое число б/г молекул растворяемого вещества. Изменение полного термодина­мического потенциала всей системы 6Ф равно сумме изменений потенциала раствора и чистого растворяемого вещества. Поскольку к раствору добавляется б/г молекул растворенного вещества, то изменение его термодинамического потенциала есть

бФ_расг = ^Г"^Тб/г = р,'бп,

где и.'—химический потенциал растворенного вещества в растворе. Изменение потенциала Ф₀ чистого растворяемого вещества равно

6Ф₀ = — ~ б/г = — ьцб/г,

так как число его молекул уменьшается на б/г (р.₀—химический потенциал чистого растворяемого вещества). Следовательно, полное изменение термодинамического потенциала при рассматриваемом процессе равно

бФ = бп(ц' —цо). (91,1)

Подставив сюда и.' из (87,5), получим

6Ф = — Т б/г 1п^с°^(Р; ^Т), (91,2)

где величина

с₀(Р, Т) = е ^т (91,3)

есть растворимость, т. е. концентрация насыщенного раствора (раствора, находящегося в равновесии с чистым растворяемым веществом). Это ясно из того, что в равновесии Ф должно иметь минимум, т.е. должно быть 6Ф = 0. Формулу (91,3) можно по­лучить и непосредственно из условия равновесия раствора с чистым растворяемым веществом, т. е. из равенства химических потен­циалов растворяемого вещества—чистого и в растворе (следует, однако, заметить, что с₀ может быть отождествлено с концентра­цией насыщенного раствора только в том случае, если с₀ мало, так как все формулы последних параграфов применимы только к малым концентрациям).

Полученное выражение определяет искомую работу: величина | 6Ф | есть максимальная работа, которая может быть совершена за счет растворения б/г молекул; эта же величина есть мини­мальная работа, которую необходимо затратить для того, чтобы из раствора концентрации с выделить бя молекул растворенного вещества.

Теперь уже не представляет труда вычислить поглощение тепла 8Q_P при растворении при постоянном давлении (если 8Q_P < 0, то это значит, что тепло выделяется). Количество тепла, поглощающееся при процессе, происходящем при постоянном давлении, равно изменению тепловой функции (§ 14). Поскольку, с другой стороны,

\дТ Т,

то имеем¹)

Щ_Р = -Т*(Щ_р. (91,4)

Подставляя в эту формулу выражение (91,2), найдем искомое количество тепла

SQ_P= ТЧпЩ^-. (91,5)

Таким образом, тепловой эффект растворения связан с зависи­мостью растворимости от температуры. Мы видим, что 8Qp просто пропорционально бя; поэтому эта формула применима и к рас­творению любого конечного количества вещества (до тех пор, разумеется, пока раствор слабый). Количество тепла, поглощаю­щееся при растворении я молекул, равно

Q_p = _nT2^pL. (91,6)

Определим еще изменение объема при растворении, т. е. раз­ность между объемом раствора и суммой объемов чистого рас­творяемого вещества и растворителя, в котором оно растворяется. Вычислим это изменение SV для растворения бя молекул. Объем есть производная от термодинамического потенциала по давлению. Поэтому изменение объема равно производной по давлению от изменения термодинамического потенциала:

&У = §р8Ф. (91,7)

Подставляя 6Ф из (91,2), находим

SV = —T6n^lnc₉. (91,8)

В заключение заметим, что формула (91,6) находится в соот­ветствии с принципом Ле-Шателье. Предположим, например, что

^г) Аналогичная формула для количества тепла- при процессе, происходя­щем при постоянном объеме:

Wv=-^t*{wt)_v- ⁽⁹¹'^4а>

Qp отрицательно, т. е. при растворении тепло выделяется. Рас­смотрим насыщенный раствор; если его охладить, то, согласно принципу Ле-Шателье, растворимость должна повыситься так, чтобы произошло дальнейшее растворение. При этом выделится тепло, т. е. система как бы противодействует выводящему ее из равновесия охлаждению. То же самое следует и из (91,6), так как в данном случае дс„/дТ отрицательно. Аналогичные рассуж­дения доказывают согласие с принципом Ле-Шателье и форму­лы (91,8).

Задачи

1. Найти максимальную работу, которая может быть произведена при об-
разовании насыщенного раствора.

Решение. До растворения термодинамический потенциал чистого раство­рителя был N\i₀, а чистого растворяемого вещества пц'о. Потенциал всей си­стемы был <!>! = N\i₀ + п\хо. После растворения термодинамический потенциал

будет Ф_г = Л^₀ + пГ In ^-{-nty. Максимальная работа

R_m» = <tf₁-O_i=-nTln^+n(_Vi-^)=nT ln^b

(эту величину можно получить и интегрированием выражения (91,2)). Если об­разуется насыщенный раствор, т. е. с = с₀ и n = Nc=Nc₀, то

R_mx = nT = Nc,T.

2. Найти минимальную работу, которую нужно произвести для того, чтобы,
выделив из раствора с концентрацией с_г часть растворителя, довести его кон-
центрацию до с₂.

Решение. До выделения термодинамический потенциал раствора был

Ф₁ = Л?(х₀ + Л?с₁Г In ^-+Nc^

(число молекул растворенного вещества было Ncj; N—первоначальное число молекул растворителя). Для того чтобы довести концентрацию раствора до с₂, надо выделить из него N (1—Ci/c₂) молекул растворителя. Сумма термодинами­ческих потенциалов оставшегося раствора и выделенного растворителя дает

Ф₂ = NyL₀ + Ncj In ^- + Ncrf.

Минимальная работа

/?„,„=ф₁-ф₁=л?с₁г in h..

^ci

§ 92. Растворы сильных электролитов

Метод разложения термодинамических величин по степеням концентрации, использованный в предыдущих параграфах, совер­шенно непригоден в важном случае растворов сильных электро­литов, т. е. веществ, которые при растворении почти нацело диссоциируют на ионы. Медленное убывание кулоновских сил взаи­модействия между ионами с увеличением расстояния приводит к появлению членов, пропорциональных концентрации в степени более низкой, чем вторая (фактически—степени 3/2).

Легко видеть, что задача об определении термодинамических величин слабого раствора сильного электролита сводится к рас­смотренной в § 78 задаче о полностью ионизованном газе (P. Debye, Е. Hiickel, 1923). В этом можно убедиться, отправляясь от ос­новной статистической формулы для свободной энергии (31,5). Будем производить интегрирование в статистическом интеграле в два этапа. Сначала проинтегрируем по координатам и импульсам молекул растворителя. Тогда статистический интеграл примет вид

где интегрирование распространяется теперь только по фазовому пространству частиц электролита, a F (р, q) есть свободная энер­гия растворителя с «вставленными» в него ионами, координаты и импульсы которых играют роль параметров. Как известно из электродинамики, свободная энергия системы зарядов в среде (при заданных объеме и температуре последней) получается из энергии зарядов в пустом пространстве делением произведений каждых двух зарядов на диэлектрическую постоянную среды е¹). Поэтому второй этап вычисления свободной энергии раствора совпадает с вычислениями, произведенными в § 78.

Таким образом, искомый вклад сильного электролита в сво­бодную энергию раствора дается, согласно (78,12), выражением

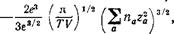
где суммирование производится по всем сортам ионов в растворе; в соответствии с обозначениями в этой главе посредством п_а обоз­начается полное число ионов сорта а (во всем объеме раствора). Этим же выражением определяется вклад в термодинамический потенциал, рассматриваемый при заданных температуре и дав­лении. Вводя молекулярный объем растворителя v(P, Т) посред­ством V«Nv, напишем термодинамический потенциал раствора в виде

ф.^+х („.г +м,) (£ г * (

¹) Это утверждение подразумевает, что расстояния между ионами велики по сравнению с молекулярными размерами. Но мы знаем из § 78, что в рас­сматриваемом приближении основной вклад в термодинамические величины происходит именно с этих расстояний.

' ''(92,1)

По обычным правилам отсюда можно найти любые термодинами­ческие свойства раствора электролита.

Так, для вычисления осмотического давления пишем хими­ческий потенциал растворителя:

Подобно тому, как это было сделано в § 88, находим отсюда осмотическое давление (на границе с чистым растворителем):

A^=_TL^—^m{t} ' ^(92>3)

Тепловая функция раствора: д Ф'

^W-------- ^Т2\дТТ Jp

(92,4)

Отсюда можно найти теплоту растворения Q, выделяющуюся при разведении раствора (при постоянных Р и Т) очень большим количеством растворителя (так что концентрация стремится к нулю). Это количество тепла дается изменением тепловой функции при процессе. Линейные по числу частиц члены, очевидно, выпадают из соответствующей разности, и мы находим из (92,4)

Единственное условие применимости полученных формул со­стоит в требовании достаточной малости концентрации. Действи­тельно, тот факт, что электролит является сильным, означает, что энергия притяжения между ионами различного сорта всегда меньше Т. Отсюда следует, что энергия взаимодействия будет во всяком случае мала по сравнению с Г на расстояниях, больших по сравнению с молекулярными. Между тем условие слабости раствора (n<^.N) означает именно, что среднее расстояние между ионами велико по сравнению с молекулярными размерами. Поэтому из этого условия автоматически следует соблюдение условия слабости взаимодействия, выражаемого неравенством

(ср. (78,2)) и лежащего в основе принятых в § 78 приближений.

Задача

Найти изменение растворимости сильного электролита (которая предпола­гается малой) при добавлении в раствор определенного количества другого элек­тролита (причем все ионы последнего отличны от ионов основного электролита).

Решение. Растворимость (т. е. концентрация насыщенного раствора) силь­ного электролита определяется уравнением

Здесь u,_TB—химический потенциал чистого твердого электролита, a v_a—число ионов сорта а в одной молекуле электролита. При добавлении к раствору по­сторонних ионов химические потенциалы собственных ионов изменятся благо­даря изменению суммы 2ⁿ6^zl>> ^{в К0Т0}РУ^Ю должны быть включены все при­сутствующие в растворе ионы. Определив растворимость с₀ посредством n_aIN = = v_ac₀, мы найдем ее изменение путем варьирования выражения (1) при задан­ных Р и Т:

Сумма под знаком вариации включает в себя только ионы добавленных сортов-Обратим внимание на то, что в рассмотренных условиях растворимость повы­шается.

§ 93. Смесь идеальных газов

Аддитивность термодинамических величин (таких, как энергия, энтропия и т. п.) имеет место лишь постольку, поскольку можно пренебречь взаимодействием отдельных частей тела. Поэтому для смеси нескольких веществ — например смеси нескольких жидкостей — термодинамические величины не будут равны суммам термодина­мических величин отдельных компонент смеси.

Исключение представляет смесь идеальных газов, так как вза­имодействием их молекул можно по определению пренебречь. Энтропия, например, такой смеси равна сумме энтропии каждого из входящих в состав смеси газов, как если бы других газов не было, а каждый из газов имел бы объем, равный объему всей смеси, и, следовательно, давление, равное парциальному дав­лению данного газа в смеси. Парциальное давление i-ro газа Р_{ выражается через.давление Р всей смеси следующим образом:

где N — полное число молекул в смеси, a N_{—число молекул i-ro газа. Поэтому согласно (42,7) энтропия смеси двух газов равна

S = N₁\n%- + N₂ In ^-NJi (T)-NJ', (T), (93,2)

или, согласно (42,8),

S = - JV_t In Р, - N₂ In Р₂ - N_1%[(Т) - N_i%2(T) =

^-(N^N^lnP-NAn^—NJn^—N^m-N^iT).

(93,3)

Свободная энергия смеси равна, согласно (42,4),

F = — N₁T ln-^-—N₂T In ^щЛ-NJ,(T) + NJ₂ (Г). (93,4)

Аналогично для потенциала Ф находим с помощью (42,6) Ф = NJ In Р_г + N₂T In Р₂ + N_lXl (Т) + N_2%2 (Т) =

= N,(Т In Р + _Xl) + N₂ (ТIn Р +_Ъ) + N,T In 4- + N₂T In.

(93,5)

Из этого выражения видно, что химические потенциалы обоих газов в смеси:

р_х = ТInP₁+_Xl = ТШР+_Ъ + ТIn4",

VL_t = T\nP_t+%_t = TlnP + %_t + Tln^-,

т. е. каждый из них имеет такой же вид, какой имел бы химиче­ский потенциал чистого газа с давлением Р_х или Р₂.

Отметим, что свободная энергия смеси газов (93,4) имеет вид

F = F₁(N_U V, Т) + F₂(N₂,V, Т),

где F_lt F₂—свободные энергии первого и второго газов как функ­ции числа частиц, объема и температуры; для термодинамического же потенциала аналогичное равенство не справедливо—потен­циал Ф смеси имеет вид

Ф = Ф_г (N_lt Р,Т)+Ф₂ (.ЛГ₂, Р, Т) + NJ In -^L + N₂T In.

Предположим, что мы имеем два различных газа с числами частиц iVj и N₂, находящихся в сосудах с объемами V_x и V₂, с одинаковыми температурами и одинаковыми давлениями. Затем оба сосуда соединяются и газы смешиваются, причем объем смеси де­лается равным Vj + Vsj, а давление и температура остаются, оче­видно, прежними. Энтропия, однако, при этом меняется; действи­тельно, до смешения энтропия обоих газов, равная сумме их энтро­пии, была

So = N, In^е^ + N_s In ^ - NJi (Т) - ВД (Т).

После смешения энтропия согласна (93,2) есть

5 = N_x In (V_t + V_t) + N₂\n-^- (V, + V₂) - Njl - ВД. Изменение энтропии

'1 У 2

или, поскольку при одинаковых давлениях и температурах объемы пропорциональны числу частиц:

AS = NAn-^- + N₂ln~. (93,7)

Эта величина положительна, т. е. энтропия при смешении увели­чивается, как и должно было быть ввиду очевидной необратимости процесса. Величину AS называют энтропией смешения.

Если бы оба газа были одинаковы, то энтропия после соедине­ния сосудов была бы

S = (N_l + N_i) In I^-iN, + N,)f.

v, + v₂ v_t v₂. и поскольку _N ^_N ~W~⁼~Fr(^{B СИЛ}У Р^{авенства} давлении и темпе­ратур), изменение энтропии было бы равно нулю.

Таким образом, изменение энтропии при смешении связано именно с различием молекул смешиваемых газов. Это соответ­ствует тому, что необходимо затратить некоторую работу, для того чтобы отделить обратно молекулы одного газа от молекул другого.

§ 94. Смесь изотопов

Своеобразными «растворами» являются смеси различных изото­пов (в любом агрегатном состоянии). Мы будем ниже говорить для простоты и определенности о смеси двух изотопов какого-либо элемента, хотя те же результаты относятся и к смеси любого числа изотопов, а также к сложным веществам (химическим соединениям), различные молекулы которых содержат различные изотопы.

В классической механике различие между частицами изото­пов сводится к различию в их массах; законы же взаимодействия атомов изотопов совершенно одинаковы. Это обстоятельство позво­ляет весьма просто выразить термодинамические величины смеси через термодинамические величины чистых изотопов. При вычисле­нии статистического интеграла смеси отличие сводится в основном к тому, что приходится делить элемент фазового объема не на N1,

как у чистого вещества, а на произведение JV_X! N_t\ факториалов чисел частиц обеих компонент смеси. Это приводит к появлению в свободной энергии лишних членов

N,T In ^-+N₂T In 4f-

(где N — А/_г + N₂), соответствующих энтропии смешения, о кото­рой в случае смеси газов шла речь в § 93.

Такие же члены появятся и в термодинамическом потенциале смеси, который может быть написан в виде

Ф = NJ In + NJ In 4г + Л^о! + ЛГ₂ц_оа. (94,1)

Здесь ц.₀₁, р₀₂ —химические потенциалы каждого из чистых изо­топов; они отличаются друг от друга только пропорциональным температуре членом:

(х_в1-11_и=-|-Г1п-^., (94,2)

где т₁, т_г—массы атомов обоих изотопов (эта разница возникает при интегрировании в статистическом интеграле по импульсам ато­мов; в случае газов (94,2) есть просто умноженная на Т разность химических постоянных).

Разность (94,2) одинакова для всех фаз данного вещества. По­этому уравнение фазового равновесия (условие равенства хими­ческих потенциалов фаз) для различных изотопов оказывается одинаковым. В частности, можно утверждать, что в классическом приближении упругости насыщенных паров различных чистых изотопов одинаковы.

Так просто обстоит дело лишь постольку, поскольку вещество может быть описано с помощью классической статистики. В кванто­вой же теории различие между изотопами становится значительно более глубоким в связи с различием колебательных и вращатель­ных уровней молекул, различием ядерных спинов и т. п.

Существенно, однако, что и при учете первых поправочных членов в термодинамических величинах (члены порядка Й²; см. § 33) термодинамический потенциал смеси может быть написан в виде (94,1). Действительно, эти члены имеют вид суммы, причем каж­дое из слагаемых содержит массу лишь одного из атомов (см. формулу (33,15) для свободной энергии). Поэтому эти слагаемые можно сгруппировать так, чтобы включить в химические потен­циалы ц₀₁ и ц₀₂; в результате формула (94,1) (но, разумеется, не (94,2)) останется в силе.

Обратим внимание на то, что термодинамический потенциал (94,1) имеет формально такой же вид, как для смеси двух про­извольных газов (§ 93). Смеси, обладающие этим свойством, назы­вают идеальными. Таким образом, смеси изотопов являются идеаль­ными с точностью до членов порядка %² включительно. В этом смысле смеси изотопов представляют собой исключительный слу­чай, так как конденсированные смеси различных веществ (не изотопов) могут быть идеальными лишь в весьма грубом прибли­жении.

В пределах применимости формулы (94,1) можно сделать опре­деленные заключения об упругости паров изотопов над их кон­денсированной смесью. Химические потенциалы обеих компонент этой смеси равны

ц^Пп^-f u._OI, p_a = Tlnc_s + Li_oa

(где c^NjN, c₂ = N₂lN—концентрации изотопов). Приравнивая их химическим потенциалам в газообразной фазе (имеющим вид Т In Р₁ + Xi (Т) и Т In Р₂ + %₂ (Т)), найдем для парциальных упру-гостей пара

Л = Л,А, Р_ш = Р_0Лс„ (94,3)

где Р₀₁ и Р₀₂ обозначают упругости пара каждого из чистых изо­топов (при данной температуре). Таким образом, парциальные упругости пара обоих изотопов пропорциональны их концентра­циям в конденсированной смеси.

Что касается упругостей насыщенного пара чистых изотопов, то, как уже было указано, в классическом приближении Р₀₁ = Р₁₁₂. При учете же квантовых эффектов появляется различие между ними. Оно не может быть вычислено в общем виде для любых веществ. Такое вычисление может быть сделано лишь для одно­атомных элементов (благородные газы) с точностью до членов порядка fa (К- Herzfeld, Е. Teller, 1938).

Поправка к термодинамическому потенциалу жидкой фазы определяется формулой (33,15) *); относя его к одному атому, найдем химический потенциал

М-И-кл-т- _24тГ г,

*) Снова пользуемся тем, что малые добавки к различным термодинами­ческим потенциалам, будучи выражены через соответствующие переменные, равны друг другу (§ 15).

где Т*—средний квадрат силы, действующей в жидкости на один атом со стороны остальных атомов. Химический же потенциал газа остается равным своему классическому выражению, так как взаимодействием частиц (атомов) газа можно пренебречь. Прирав­нивая химические потенциалы жидкости и газа, найдем поправку

к классическому значению упругости пара, а интересующая нас разность упругостей пара двух изотопов окажется равной

^рм—^р«* ^{= р}о-Ш*{щ — щ)> (⁹⁴>⁴)

где Р₀—общее классическое значение P_oi и Р₀₂. Мы видим, что знак этой разности определяется разностью обратных значений масс атомов изотопов, причем упругость паров легкого изотопа больше, чем у тяжелого.

§ 95. Давление пара над концентрированным раствором

Рассмотрим равновесие раствора с находящимся над ним паром, который состоит, вообще говоря, также из обоих веществ. При этом раствор может быть как слабым, так и сильным, т. е. коли­чества обоих веществ в нем могут быть произвольными. Напом­ним, что результаты, полученные в § 89, относились только к сла­бым растворам.

Поскольку раствор и пар находятся в равновесии друг с дру­гом, химические потенциалы р_х и р₂ обеих компонент в растворе и в паре равны друг другу. Если обозначить количества частиц обоих веществ в растворе через Щ и N$, то можно написать для раствора выражение (24,14) в виде

dQ = — Щ dp _х—Щ dp ₂—S^p dT — Р dV^p. (95,1)

Здесь S^p и V^p—энтропия и объем раствора; температура Т и да­вление Р одинаковы для раствора и для пара.

Предположим, что пар над раствором настолько разрежен, что может рассматриваться как идеальный газ; давление его мало. На этом основании пренебрегаем в (95,1) членами, пропорциональ­ными Р, т. е. Р dV и dQ. Будем сначала рассматривать все про­изводные при постоянной температуре. Тогда получаем из (95,1)

JVPdp^ + A^dp^O. (95,2)

С другой стороны, для газообразной фазы

_Vi = ThiP_l + x₁(T),

М = Т\пР,+_х, (Г).

Здесь Р₁ и Р_г — парциальные давления обеих компонент пара. Дифференцируя эти выражения (при Т = const), находим

d\il = Td\nP_lt dp^r = rdlnP₂.

Подставляя это в (95,2), получаем

NfdlnP₁ + NtdlnP, = 0. (95,3)

растворы

[ГЛ. IX

Введем концентрацию £ раствора как отношение числа частиц первой компоненты к полному числу частиц:

и аналогично—концентрацию х пара. Парциальные давления Р_х и Р₂ равны произведениям полного давления Р пара на концентра­ции соответствующих компонент, т. е. P_t = xP, Р₂ = (1—х) Р. Подставляя все это в (95,3) и деля это уравнение на полное число Ы = Щ-\-Щ частиц в растворе, находим

Id In Рх+ (1 — I) d In Р (1 — х) = 0,

откуда

d\nP= *~^l,dx,

х(1 — х) '

или

| ₌ *_*((95,4)

Это уравнение связывает концентрации раствора и пара с зависимостью упругости пара от его концентрации.

Еще одно общее соотношение можно получить, рассматривая температурную зависимость величин. Напишем условие равенства химических потенциалов в паре и растворе для одной из ком­понент, скажем первой:

_г_ с7Ф^р ^ ~ dNl '

Разделив обе стороны равенства на Т и помня, что производная по числу частиц берется при постоянной температуре, пишем:

Ц а Ф^р Т dNl Т

Возьмем теперь от обеих сторон равенства полную производную по температуре. При этом можно с достаточной точностью счи­тать, что термодинамический потенциал конденсированной фазы (раствора) не зависит от давления. Замечая также, что частная производная по температуре

_{дт т} — Т² \ дТ) Г»'

получим следующее соотношение:

ainP^ _{= г}_а^р_ (95,5)

дТ

Здесь w{—молекулярная тепловая функция газа первого веще­ства; производная же dW^pJdN^p определяет изменение тепловой функции раствора при добавлении к нему одной молекулы этого вещества. Величина, стоящая в правой стороне равенства (95,5), представляет собой, следовательно, тепло, поглощающееся при переходе из раствора в пар одной частицы первого вещества.

Для чистого первого вещества соотношение (95,5) превращается в обычное уравнение Клапейрона — Клаузиуса

где Р₁₀—упругость пара первого чистого вещества, a»f—его мо­лекулярная тепловая функция в жидком состоянии. Вычитая это равенство почленно из уравнения (95,5), получим окончательно следующее соотношение:

где Oj = — wf—молекулярная теплота разбавления—количе­ство тепла, поглощающееся при переходе в раствор одной частицы из жидкого первого вещества. Такое же соотношение можно, разумеется, написать и для второго вещества.

§ 96. Термодинамические неравенства в растворах

В § 21 было показано, что тело может существовать лишь в таких состояниях, в которых выполняются определенные условия—так называемые термодинамические неравенства. Эти условия были, однако, выведены нами для тел, состоящих из одинаковых частиц. Произведем теперь аналогичное исследование для растворов, при­чем мы ограничимся случаем смеси всего двух веществ. •

В § 21 мы пользовались в качестве условия равновесия не максимальностью энтропии замкнутого тела в целом, а эквива­лентным ему условием, требующим положительности минималь­ной работы, необходимой для того, чтобы вывести какую-либо малую часть тела из состояния равновесия в любое другое близ­кое состояние.

Аналогично поступим и теперь. Выделим из раствора неко­торую малую часть; числа частиц растворителя и растворенного вещества в ней пусть будут Nun. В состоянии равновесия тем­пература, давление и концентрация в этой части равны значе­ниям тех же величин для остального раствора (играющего роль внешней среды). Определим минимальную работу, которую необ­ходимо произвести для того, чтобы выделенная нами часть, со­держащая определенное число N частиц растворителя, приобрела температуру, давление и число частиц растворенного вещества, отличающиеся на малые (но конечные) величины 67, 6Р и 8п от их равновесных значений.

Дата добавления: 2014-11-07