Ol — V2X 21 страница

F — — 1.9^1 F- ^{3 GM2} F - ^{3 GM2} ППЙ 1П\

■'-'гр 7 R ' 7 R ' ^полн— 7 ' (.^Оо,

В ультрарелятивистском же случае имеем п = 3, так что

£r_P = -£ = -4if\ £полн=о. (108,11)

Полная энергия равна в этом случае нулю в соответствии с изло­женными в предыдущем параграфе качественными соображениями о равновесии такого тела ²).

§ 109. Равновесие нейтронной сферы

^г) Заметим, что в этом случае 2£ = —£_гр в соответствии с известной из механики теоремой вириала, примененной к системе частиц, взаимодействующих по закону Ньютона (см. I, § 10) ²) Напомним, во избежание недоразумений, что релятивистская внутренняя энергия £ (а с нею и £_Полн ^в (108,11)) включает в себя также и энергию покоя частиц (создающих'давление Р). Если же определить £_Поли ^как «энергию связи» тела (отсчитываемую от энергии вещества, рассеянного по пространству), то энергия покоя частиц должна быть вычтена из нее.

Для тела с большой массой существуют две возможности рав­новесного состояния. Одна из них соответствует электронно-ядер­ному состоянию вещества, как это предполагалось при численных оценках в § 107. Другая же соответствует нейтронному состоянию вещества, в котором почти все электроны захвачены протонами и вещество можно рассматривать как нейтронный газ. При достаточно

больших массах тела вторая возможность во всяком случае должна стать термодинамически более выгодной, чем первая (W. Baade, F. Zwicky, 1934). Хотя превращение ядер и электронов в сво­бодные нейтроны и связано со значительной затратой энергии, но при достаточно большой полной массе тела эта затрата будет с избытком компенсирована освобождением гравитационной энергии, связанным с уменьшением размеров и увеличением плотности тела.

Прежде всего исследуем вопрос о том, при каких условиях нейтронное состояние тела вообще может соответствовать какому бы то ни было термодинамическому равновесию (хотя бы и ме-тастабильному). Для этого исходим из условия равновесия Р+^«9 = const, где р—химический потенциал (термодинамиче­ский потенциал, отнесенный к одному нейтрону), т_п—масса ней­трона, ф—гравитационный потенциал.

Поскольку на границе тела давление должно быть равно нулю, ясно, что в некотором внешнем слое вещество будет иметь не­большие давление и плотность и, следовательно, будет находиться в электронно-ядерном состоянии. Хотя толщина такой «оболочки» и может оказаться сравнимой с радиусом внутреннего плотного нейтронного «ядра», тем не менее благодаря значительно меньшей плотности этого слоя его полную массу можно считать малой по сравнению с массой ядра¹).

Сравним значения ц.-|-т„ф в двух местах: в плотном ядре вблизи его границы и вблизи внешней границы оболочки. Грави­тационный потенциал в этих точках можно считать равным — GM/R и —GM/R', где R и R' — радиусы ядра и оболочки, а М—масса ядра, совпадающая в нашем приближении с полной массой тела. Что касается химического потенциала, то он в обоих случаях определяется в основном внутренней энергией (энергией связи) соответствующих частиц, большой по сравнению с их теп­ловой энергией. Поэтому разность обоих химических потенциа­лов можно положить равной просто разности приходящейся на единицу атомного веса энергии покоя нейтрального атома (т. е. ядра и Z электронов) и энергии покоя нейтрона; обозначим эту вели­чину посредством Д. Таким образом, приравнивая значения р. + т„ф в двух рассматриваемых местах, получим

Отсюда видно, что, каким бы ни был радиус R', масса и радиус нейтронного ядра должны удовлетворять неравенству

m_nMG R

> А.

(109,1)

С другой стороны, применив результаты § 107 к сферическому телу, состоящему из вырожденного (нерелятивистского) нейтрон­ного газа, мы найдем, что М и R связаны друг с другом соот­ношением

MR³=9l,9-^-~ =3,6-10³Окл? (109,2)

G³m„

(формула (107,10), в которой надо заменить т_в и т' на т_п). Выразив отсюда М через R и подставив в (109,1), получим не­равенство для М. Численно оно дает

М > ~ 0,2О.

Так, взяв значение А для кислорода, получим М > 0,17 0, для же­леза М>0,18О- Таким массам соответствуют радиусы^?<26км*).

Полученное неравенство определяет нижний предел масс, за которым нейтронное состояние тела вообще не может быть устой­чивым. Однако оно еще не обеспечивает полной устойчивости состояния, которое может оказаться метастабильным. Для опре­деления границы метастабильности надо сравнить полные энергии тела в обоих состояниях: нейтронном и электронно-ядерном. С одной стороны, переход всей массы М из электронно-ядерного состояния в нейтронное требует затраты энергии

4-А

для компенсации энергии связи ядер. С другой стороны, при этом произойдет освобождение энергии за счет сжатия тела; согласно формуле (108,10) этот выигрыш в энергии равен

3GM² (J_______ 1_

7 \R_a Re

где R„—радиус тела в нейтронном состоянии, определяемый формулой (109,2), a R_e — радиус тела в электронно-ядерном состо­янии, определяемый формулой (107,10). Поскольку R_e^>R_n, то величиной \/R_e можно пренебречь, и мы получаем следующее условие, обеспечивающее полную устойчивость нейтронного состо­яния тела (индекс у R_n опускаем):

> Д. (109,3)

^г) Подчеркнем, что численным оценкам в этом параграфе, основанным на простых предположениях о структуре тела, не следует придавать слишком бук­вальный астрофизический смысл.

Сравнивая: это условие с условием (109,1) и учитывая (109,2), мы видим, что определяемый неравенством (109,3) нижний предел массы в (7/3)^3/4 = 1,89 раз выше, чем получающийся из (109,2).

Численно граница метастабильности нейтронного состояния ле­жит, таким образом, при массе

М ж 1/3 О

(и радиусе R «22 км)^х).

Перейдем к вопросу о верхнем пределе значений массы, при которых нейтронное тело может находиться в равновесии. Если мы применили бы результаты § 107 (формулу (107,17) с т_п вмес­то т'), то мы получили бы для этого предела значение 6 О.

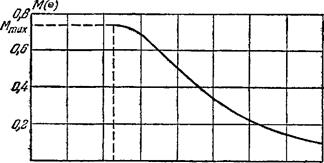
^ 4 SR_mi0r2 15 20 24 ££ 32

Д. км

Рис. 52.

В действительности, однако, эти результаты неприменимы к дан­ному случаю по следующей причине. В релятивистском нейтрон­ном газе кинетическая энергия частиц порядка величины (или больше) энергии покоя, а гравитационный потенциал ф~с²²). Ввиду этого становится незаконным применение ньютоновской теории тяготения, и вычисления должны производиться на основе общей теории относительности. При этом, как мы увидим ниже, оказывается, что ультрарелятивистский случай вообще не дости­гается; поэтому вычисления должны производиться с помощью точного уравнения состояния вырожденного ферми-газа (см. за­дачу 3 к § 61).

^х) Средняя плотность тела при этом равна 1,4-10¹³ г/си³, так что нейтрон­ный газ действительно еще можно считать нерелятивистским, и использова­ние применяемых нами формул еще законно. ²) В электронном же релятивистском газе кинетическая энергия частиц сравнима с энергией покоя электронов, но все еще мала по сравнению с энер- гией покоя ядер, составляющих основную массу вещества. ³) За подробностями вычислений отсылаем к оригинальной статье J. R.Oppenheimer, G. М. Volkoff, Phys, Rev. 55, 374 (1939).

Вычисления производятся путем численного интегрирования уравнений центрально-симметрического статического гравита­ционного поля и приводят к следующим результатам³).

Предельное значение массы равновесного нейтронного шара оказывается равным всего Ж_тах=0,7бО, причем это значение достигается уже при конечном (равном /?_mj_n = 9,4 км) его ради­усе; на рис. 52 изображен график получающейся зависимости массы М от радиуса R. Устойчивые нейтронные сферы большей массы или меньшего радиуса, таким образом, не могут сущест­вовать. Следует указать, что под массой М мы понимаем здесь произведение M = Nm_n, где N — полное число частиц (нейтронов) в сфере. Эта величина не совпадает с гравитационной массой те­ла Af_rp, определяющей создаваемое им в окружающем простран­стве гравитационное поле. Благодаря «гравитационному масс-де-фекту» в устойчивых состояниях всегда М_гр < М (в частности,

при R = R_mia M_rp = 0,95AT)i).

Что касается вопроса о поведении сферического тела с мас­сой, превышающей М_тах, то заранее ясно, что оно должно стре­миться неограниченно сжиматься. Исследование характера такого неудержимого гравитационного коллапса- изложено в другом то­ме этого курса (см. II, §§ 102—104).

*) Точка R = R_m\n ^на Р^ис- 52 есть 'в действительности точка максимума кривой M = M(R). Эта кривая продолжается за точку максимума в виде за­кручивающейся спирали, асимптотически приближающейся к определенному центру. Параметром, монотонно возрастающим вдоль всей кривой, является плотность в центре сферы, стремящаяся к бесконечности для сферы, соответ­ствующей предельной точке спирали (Н. А. Дмитриев, С. А. Холин, 1963). Вся часть кривой при R < R_m-_ln, однако, не соответствует устойчивому со­стоянию сферы. Изложение соответствующего исследования — см. Н. А. Дмитриев, С. А. Хо­лин, Вопросы космогонии, т. 9, 1963; Б. К. Гаррисон, К- С. Торн, М. Ва­тт, Дж. А. Уилер, Теория гравитации и гравитационный коллапс, «Мир», 1967 (University of Chicago Press, 1965). ²) См. Я- Б. Зельдович, ЖЭТФ 42, 641 (1962).

Следует отметить, что принципиальная возможность гравита­ционного коллапса, неизбежного (для рассматриваемой модели сферического тела) при м > м_тах, не ограничена в действитель­ности большими массами. «Коллапсирующее» состояние сущест­вует для любой массы, но при м < М_ты оно отделено от ста­тического равновесного состояния очень высоким энергетическим барьером²).

ГЛАВА XII

ФЛУКТУАЦИИ

§110. Распределение Гаусса

Уже много раз подчеркивалось, что физические величины, характеризующие равновесное макроскопическое тело, практи­чески всегда с очень большой точностью равны своим средним значениям. Однако, как ни малы отклонения от средних значе­ний они все же происходят (величины, как говорят, флуктуи­руют), и возникает вопрос о нахождении распределения веро­ятностей этих отклонений.

Рассмотрим какую-либо замкнутую систему, и пусть х есть некоторая физическая величина, характеризующая систему в це­лом или какую-либо ее часть (в первом случае это, конечно, не должна быть величина, остающаяся для замкнутой системы стро­го постоянной, как, например, ее энергия). В дальнейшем будет удобно полагать, что среднее значение х уже вычтено из х, так что везде ниже предполагается, что jc = 0.

Изложенные в § 7 рассуждения показали, что если рассматри­вать формальным образом энтропию системы как функцию от точных значений энергий подсистем, то функция e^s будет давать распределение вероятностей для этих энергий (формула (7,17)). Легко, однако, заметить, что в этих рассуждениях не были ис­пользованы какие-либо специфические свойства энергии. Поэтому такие же рассуждения приведут к результату, что вероятность величине х иметь значение в интервале между х и x-\-dx про­порциональна e^Su), где5(х)—энтропия, формально рассматри­ваемая как функция точного значения х. Обозначив вероятность посредством w (х) dx, имеем^г)

w (х) = const-e^S(*>. (110,1)

*) Эта формула была впервые применена к исследованию флуктуации А. Эйнштейном (1910).

Прежде чем приступить к исследованию этой формулы, оста­новимся на вопросе о пределах ее применимости. Все рассужде­ния, которые привели к формуле (110,1), неявно подразумевают

классичность поведения величины х¹). Поэтому надо найти усло­вие, допускающее пренебрежение квантовыми эффектами.

Как известно из квантовой механики, между квантовыми неопределенностями энергии и какой-либо величины х имеет место соотношение

АЕ Ах ~ %х,

где х—классическая скорость изменения величины х (см. III, § 16).

АЕ Ах

Пусть т—время, характеризующее скорость изменения инте­ресующей нас величины х, которая имеет неравновесное значе­ние²); тогда х ~ х/т, так что

Ясно, что говорить об определенном значении величины х мож­но лишь при условии малости ее квантовой неопределенности: Ах<^,х, откуда

Таким образом, квантовая неопределенность энергии должна быть велика по сравнению с %/х. Энтропия же системы будет при этом иметь неопределенность

Для того чтобы формула (110,Д) имела реальный смысл, необ­ходимо, очевидно, чтобы неточность энтропии была мала по сравнению с единицей:

Т>\-, т>А. ₍1_10>2)

¹) Это не означает, конечно, что вся система должна быть классической. Другие (помимо х) относящиеся к ней величины могут иметь квантовый ха- рактер. ²) Время т может не совпадать со временем релаксации для установления равновесия по величине х, а быть меньше него, если величина х приближается к х, испытывая в то же время колебания. Так, если речь идет об изменении давления в небольшом участке тела (с линейными размерами ~ а), то т будет порядка величины периода звуковых колебаний с длиной волны X—а, т. е. т — а/с, где с — скорость звука.

Это и есть искомое условие. При слишком низких температурах или при слишком быстром изменении величины х (слишком ма­лом т) флуктуации нельзя рассматривать термодинамически, и на первый план выступают чисто квантовые флуктуации.

§ 110] РАСПРЕДЕЛЕНИЕ ГАУССА 365

<о.

Л2е — 0 — *=о ^и* дх²

Вернемся к формуле (110,1)- Энтропия S имеет максимум при х = х = 0. Поэтому

ds_ дх

х = 0

Величина я при флуктуациях очень мала. Разлагая S(x) в ряд по степеням х и ограничиваясь членом второго порядка, получим

S(x) = S(0)-|-x², (110,3)

где В — положительная постоянная. Подставляя в (110,1), полу­чим распределение вероятностей в виде

w (х) dx— Ае ² dx.

Нормировочная постоянная А определяется условием \w(x)dx—\;

хотя выражение для w(x) относится к малым х, но ввиду быст­рого убывания подынтегральной функции с увеличением \х| об­ласть интегрирования можно распространить на все значения от — оо до + ⁰⁰ • Произведя интегрирование, получим А = 1/^6/2^.

Таким образом, распределение вероятностей для различных значений флуктуации х определяется формулой

w(x)dx= У -2яТе ² dx. (110,4)

Распределение такого вида называется распределением Гаусса. Оно имеет максимум при х = 0 и быстро спадает с увеличением \х\ симметрично в обе стороны.

Средний квадрат флуктуации равен

<х*> ^_x*w(x)dx = ~. (110,5)

— со

Поэтому распределение Гаусса можно написать в виде

Как и следовало, w(x) имеет тем более острый максимум, чем меньше <*²>.

*) Подразумевается, конечно, что функция <р(х) мало меняется на значе­ниях х^<^>^^г и что производная dyjdx отлична от нуля при х=0.

Отметим, что по известному <х²> можно найти аналогичную величину для любой функции у(х). В виду малости х имеем¹);

§ 111. Распределение Гаусса для нескольких величин

В предыдущем параграфе мы рассматривали вероятность от­клонения какой-либо одной термодинамической величины от ее среднего значения, не интересуясь при этом значениями других величин, т. е. считая значения последних произвольными¹). Аналогичным образом можно определить вероятность одновремен­ного отклонения ряда термодинамических величин от своих сред­них значений; эти отклонения мы обозначим посредством

^Х1> ^Х2> • • • > ^Хп'

Вводим энтропию S(x₁, х_п) как функцию рассматривае­мых величин и пишем распределение вероятностей в виде wdx_x...dx_n с w из (110,1). Разлагаем 5 по степеням х,-; с точ­ностью до членов второго порядка разность S—S₀ представится в виде существенно отрицательной квадратичной формы

1 "

I, k=\

(очевидно, что Р,й = 6«). Ниже в этом параграфе мы будем опу­скать знаки суммирования и по дважды повторяющимся индек­сам везде подразумеваем суммирование (по всём значениям от 1 до п). Таким образом, пишем:

S-5₀=—(111,1)

Подставляя это выражение в (110,1), находим для искомого рас­пределения вероятностей формулу

в»=Лехр(—-g-ptt*,**). (Н1.2)

Постоянная А определяется условием нормировки ^wdx_t......dx_n=l, в котором (по той же причине, что и в § ПО) интегрирование по всем х,- можно производить в пределах от — оо до оо. Для вычисления этого интеграла поступим следую­щим образом. Произведем над величинами х,- линейное преобра­зование

*/ = (111,3)

которое превращает квадратичную форму В,*х,х_А в сумму квад­ратов x'i. Для того чтобы было

¹) Это значит, что функция S (х), которой мы пользовались в § 110, пред­ставляла собой наибольшее значение, которое энтропия может принять при заданном неравновесном значении х.

§ik^xi^xk — Х_{== XtX'ifiik,

надо, чтобы коэффициенты преобразования удовлетворяли соот­ношениям

Определитель матрицы величин, стоящих в левой стороне этого равенства, равен произведению определителя р = | $_ik | и двух определителей a = \a_ik\. Определитель же |б,-_й| = 1. Поэтому из написанного соотношения следует, что

Ра²=1. (111,5)

Якобиан линейного преобразования от переменных х,- к пере­менным х\ есть постоянная величина — определитель а. Поэтому-после проведения преобразования нормировочный интеграл рас­падается на произведение п одинаковых интегралов и с учетом (111,5) получим

Аа

^(2^ = 1.

J ехр ^ — у*'*) ^dx'

L -со

Таким образом, находим окончательно распределение Гаусса для нескольких величин в виде

Введем величины

Ц=Р«*а. (111,7)

которые назовем термодинамически взаимными с величинами х,-*). Определим средние значения произведений х,-Х_А:

<х,Х_л> = J^l; J... J х,р_их, ехр (— -I р,-*х,х^ dx_t... dx„.

Для вычисления интеграла допустим на минуту, что средние значения х,- равны не нулю, а некоторым конечным х_/0. Тогда в (111,6) надо писать х,-—х,₀ вместо х,- и, согласно определению средних значений, получим

¹) Отметим, что при линейной зависимости (111,7) эта взаимность обоюд­ная: если та же энтропия S выражена через величины X;, то dS

(Ш,7а) dS=—X_k dx_k = — _Pfti x_t dx_h = — x_td ($_ikx_k) = — x_t dX_t.

Действительно, используя (111,7), имеем

*' ⁼ (2^» J*'' J*'^exP [^—■§"?«(*/—*/»)(**—*»)] • -dx_n = x_№.

Дифференцируя это равенство по x_k0 и полагая затем снова все x_iB равными нулю, получим справа b_ik, а слева — как раз нужный нам интеграл.

Таким образом, находим

= 8_rt. (111,8)

Подставив сюда (111,7), получим: в_л;<ад-> =

°ia> откуда
<*,**> = рй\ (111,9)

где В»¹ — элемент матрицы, обратной матрице В_/А.

Наконец, определим еще <Х,Х_Й>. Согласно (111,7—8) имеем
<ВД»> = Р«= Р/,6«, т. е.

<Х,Х_Л>^_Л.. (111,10)

Легко определить также средний квадрат флуктуации любой функции ф (х₁₍..., х_п). Поскольку отклонения от средних зна­чений малы, то Аф = (ду/дх;) Ах;, где под дц>/дх; понимаются значения производных при х₁ = х₂ =... =0. Отсюда

Если флуктуации каких-либо двух величин х₍ (назовем их х_г и х₂) статистически независимы, то среднее значение <.х_гх₂У равно произведению средних значений x_t и х₂, и поскольку каж­дое из последних равно нулю, то обращается в нуль и <д:₁х₂>; по (111,9) это означает, что P{₂¹ = 0. Легко видеть, что при гаус­совом распределении вероятностей справедлива и обратная тео­рема: если <x₁x_i> = 0 (т. е. РГг¹ = 0). то флуктуации величин х_гк х₂ статистически независимы.

Действительно, распределение вероятностей w₁₂ для величин х_г и х₂ получается интегрированием распределения (111,6) по всем остальным х-; при этом получится выражение вида

о»_и = const-ехр | —2-Рп*²—Pi₈*i*2—yP^lj-

*) Для матрицы второго ранга имеем: {$«?<= РиЛ?'*'""РпРга)-

(в котором коэффициенты Р#, вообще говоря, отличны от соот­ветствующих компонент Р_(А). Применив к этому распределению формулу (111,9), найдем, что <х₁х₂> = р"₁₂~¹. Если <^₁х₂> = 0, то Pi₃^_1 = 0. Но для матрицы второго ранга обращение в нуль ком­поненты Pi₂^-1 обратной матрицы означает равенство нулю также компоненты Pi₂ прямой матрицы¹). В результате w_l2 распадается на произведение двух независимых гауссовых распределений для величин х_г и х₂, что и означает их статистическую независимость.

§ 112. Флуктуации основных термодинамических величин

Займемся теперь вычислением средних квадратов флуктуации основных термодинамических величин, относящихся к выделен­ной в теле какой_:либо малой его части. Эта малая часть должна, разумеется, содержать еще достаточно много частиц. Однако при очень низких температурах это условие может оказаться более слабым, чем условие (110,2), обеспечивающее предпола­гаемое отсутствие квантовых флуктуации; в этом случае мини­мальные допустимые размеры участков тела будут определяться именно последним условием¹). Во избежание недоразумений следует подчеркнуть, что вопрос о степени существенности кван­товых флуктуации не имеет никакого отношения к вопросу о влиянии квантовых эффектов на термодинамические величины (уравнение состояния) вещества; флуктуации могут быть класси­ческими, и в то же время уравнение состояния тела может опре­деляться квантовомеханическими формулами.

*) Так, для флуктуации давления условие %^>%/Т с т~а/с (см. примеча­ние на стр. 364) дает: а *>> Ас/Г.

Для таких величин, как энергия, объем и т. п., имеющих наряду с термодинамическим также и чисто механический смысл, понятие флуктуации само собой очевидно. Оно нуждается, однако, в уточнении для таких величин, как энтропия и темпе­ратура, определение которых неизбежно связано с рассмотрением тела в течение конечных интервалов времени. Пусть, например, S (Е, V) есть равновесная энтропия тела как функция его (сред­них) энергии и объема. Мы будем понимать под флуктуацией энтропии изменение функции S(E, V), рассматриваемой формально как функция от точных (флуктуирующих) значений энергии и объема.

Как мы видели в предыдущих параграфах, вероятность w флуктуации пропорциональна ехр5_п, где S„—полная энтропия замкнутой системы, т. е. всего тела в целом. С тем же успехом можно написать, что w пропорциональна

w со ехр AS_n,

где AS„—изменение энтропии при флуктуации. Согласно фор­муле (20,8) имеем: А5_П = — R_mijT₀, где R_min—минимальная работа, необходимая для того, чтобы обратимым образом произ­вести заданное изменение термодинамических величин данной малой части тела (по отношению к которой остальные части тела играют роль среды). Таким образом,

ауслехр (— (П2,1)

Подставим сюда для R_mia выражение

R_min = AE-T₀AS + P₀AV,

где АЕ, AS, AV—изменения энергии, энтропии и объема данной малой части тела при флуктуации, а Г, и Р₀—температура и давление «среды», т. е. равновесные (средние) значения темпера­туры и давления тела. Ниже мы будем опускать индексы нуль у всех величин, стоящих в качестве коэффициентов перед флук-туациями; везде подразумеваются их равновесные значения. Таким образом, имеем

вуслехр(^ j. (112,2)

Заметим, что в таком [виде эта формула применима к любым флуктуациям — как небольшим, так и значительным; под значи­тельными здесь подразумеваются такие флуктуации, - при кото­рых, например, АЕ сравнимо с энергией самой малой части тела, но, конечно, по-прежнему мало по сравнению с энергией тела в целом. В применении к малым флуктуациям (какими они, вообще говоря, являются) формула (112,2) дает следующее. Разлагая АЕ в ряд, получим (ср. § 21)

_АЕ_Т as + Р AV = 1 [g- (AS)² + 2^ASAV + ™ (AV)²]. Как легко убедиться, это выражение можно написать в виде

Т [^ASA (§)v + ^AyA (i)J -ji^AT-APAV)

Таким образом, получаем вероятность (112,2) флуктуации в виде

(APAV—AT AS\,,,„,.

гослехр^ 2f)' (П2,3)

Из этой общей формулы можно найти флуктуации различных термодинамических величин. Выберем сначала в качестве неза­висимых переменных V и Т. Тогда

Д₃=(|)_уАГ₊(§)_гЛ^ДГ₊(|)^,

"-(»),*+(»),»

(см. (16,3)). Подставляя эти выражения в показатель формулы (112,3), найдем, что члены с AV AT сокращаются, и остается

w слехр {(AT)² + ± [%) _т (AV)²}. (112,4)

Это выражение распадается на два множителя, зависящих только от AT или AV. Другими словами, флуктуации темпера­туры и объема статистически независимы, а потому

<АГДУ> = 0. (112,5)

Сравнивая поочередно каждый из двух множителей, на ко­торые распадается (112,4), с общей формулой (110,6) распреде­ления Гаусса, найдем следующие выражения для средних квад­ратов флуктуации температуры и объема¹):

<(ДГ)²>=Р, (112,6)

<(АУ)²> = -Г(^)_г. (112,7)

Положительность этих величин обеспечивается термодинамиче­скими неравенствами C_v > 0 и (дР/дУ)т < 0.

Выберем теперь в качестве независимых переменных в (112,3) Р и S. Тогда

Но согласно формуле dW = ТdS-\-VdP имеем

dS Jp~~dPdS~{dPjs'

^J) Если T измеряется в градусах, то <{AT)²>=kT²/C_v.

и поэтому

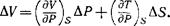
Подставляя ДУ и АГ в (112,3), находим

_w^ex_P{±(^_p)_s(APr~±-_{ASy}. (112,8)

Как и (112,4), это выражение распадается на множители, зависящие соответственно от АР и AS. Другими словами, флук­туации энтропии и давления статистически независимы*), и потому

<ASAP> = 0. (112,9)

Для средних квадратов флуктуации энтропии и давления находим

<(AS)²> = C,, (112,10)

<(АР)*>=-Г(!£)₅. (112,11)

Дата добавления: 2014-11-07