Ol — V2X 22 страница

Из полученных формул видно, что средние квадраты флук­туации аддитивных термодинамических величин — объема и энтропии —пропорциональны размерам (объему) тех частей тела, к которым они относятся. Соответственно средняя квадратичная флуктуация этих величин пропорциональна квадратному корню из объема, а относительная флуктуация — обратно пропорцио­нальна этому корню; это находится в соответствии с общими утверждениями, сделанными в § 2 (формула (2,5)). Для таких же величин, как температура и давление, обратно пропорцио­нальны корню из объема уже сами их средние квадратичные флуктуации.

Формула (112,7) определяет флуктуацию объема некоторой части тела, содержащей определенное число N частиц. Деля обе стороны равенства на N², находим флуктуацию объема, прихо­дящегося на одну частицу:

Эта величина, очевидно, не может зависеть от того, рассматри­ваем ли мы флуктуацию в постоянном объеме или для постоян­ного числа частиц. Поэтому из (112,12) можно найти флуктуацию числа частиц, находящихся в определенном выделенном в теле

!) Статистическая независимость пар величин Т, V и S, Р очевидна зара­нее из следующих соображений. Если выбрать в качестве величин ж,- (в фор­мулах § 111) x_t=AS, x₂ — AV, то соответствующими им Х[ будут (см. § 22): Х₁ = АТ/Т, Х₂= —АР/Т. Но <а:,Ха> = 0 при 1фк (согласно общей формуле (111,8)), откуда и следуют (112,5) и (112,9).

объеме. Поскольку при этом V есть заданная величина, то надо положить

Подставляя это в (112,12), находим

<(ДЛ')*> = -^(!£1.. (112,13)

V¹ \дР Jt'

Для некоторых вычислений удобно представить эту формулу в ином виде. Замечая, что производная (dV/dP)_T подразумевается взятой при постоянном" N, пишем

V¹\dPj_t,n~' [дР V Jt.n'

Но число частиц N как функция от Р, Т, V в силу соображе­ний аддитивности должно иметь вид N = Vf(P,T) (ср. § 24); другими словами, N/V есть функция только от Р и Т, и потому безразлично, производится ли дифференцирование N/V при по­стоянном N или V, так что можно написать:

\дР V)т, n V \дР)т,у~~ \дР]т. v \д\»,)т,у~ \ дц

Т, V

(мы воспользовались равенством N/V= (дР/дц)т, v, следующим из формулы (24,14) dQ =— VdP= — SdT — Nd[i). Таким обра­зом, получаем следующую формулу для флуктуации числа частиц^J):

<(ДЛ0'> = Г(4£)_Г1у. (112,14)

^г) Эту формулу можно легко получить и непосредственно из распределения Гиббса. Согласно определению средних значений имеем

n n

Продифференцировав это выражение по р. (при постоянных V и Т), получим

n п

Но dQ/dp.=—Л/, так что

^ = Y «N²> - Щ = jr < (АЛ0»>,

откуда и получается формула (112,14).

Исходя из распределения Гиббса, можно было бы получить выражения и для флуктуации других термодинамических величин.

Наряду с рассмотренными термодинамическими величинами, тело характеризуется также импульсом Р своего макроскопиче­ского движения относительно среды. В состоянии равновесия никакого макроскопического движения нет, т. е. Р=0. Движение, однако, может появиться в результате флуктуации; определим веро­ятность такой флуктуации. Минимальная работа ^_min в этом случае равна просто кинетической энергии тела

где М—его масса, v = P/M—скорость макроскопического дви­жения. Таким образом, имеем для искомой вероятности

шел ехр (—• (112,15)

Отметим, что флуктуации скорости статистически независимы от флуктуации других термодинамических величин. Средний квадрат флуктуации каждой из декартовых компонент скорости равен

<(Atg*> = ^-; (112,16)

он обратно пропорционален массе тела.

Из выведенных формул видно, что средние квадраты флукту­ации таких величин, как энергия, объем, давление, скорость, обращаются при абсолютном нуле в нуль (пропорционально пер­вой степени температуры). Это является общим свойством всех термодинамических величин, имеющих также и чисто механи­ческий смысл, но, вообще говоря, не относится к таким чисто термодинамическим величинам, как энтропия и температура.

Формула (112,6) для флуктуации температуры может быть истолкована еще и с другой точки зрения. Как мы знаем, поня­тие температуры может быть введено через посредство распределе­ния Гиббса; при этом температура рассматривается как параметр, определяющий это распределение. В применении к изолирован­ному телу распределение Гиббса полностью описывает его стати­стические свойства с той лишь неточностью, что оно дает весьма малые, но все же отличные от нуля флуктуации полной энергии тела, которых в действительности не должно быть (см. стр. 100). Напротив, если считать энергию величиной заданной, то нельзя приписывать телу вполне определенную температуру, и надо считать, что последняя испытывает флуктуации, определяющиеся формулой (112,6), в которой C_v будет теплоемкостью тела в целом. Эта величина, очевидно, характеризует точность, с которой мо­жет быть дано определение температуры изолированного тела.

Задачи

i. Найти средний квадрат флуктуации энергии (пользуясь в качестве неза­висимых переменных V и Т). Решение. Имеем

^ (*), AV+ (*), AT - [г [§\-р] А,+С„АГ.

Возводя в квадрат и усредняя, получим

<(Д£)²>=-

2. Найти <(Д№)²> (пользуясь переменными Р и S).
Решение.

_<{AW)*>=-TV*(jiy+T4:_p.

3. Найти < ДТ ДР > (пользуясь переменными К и Т).
Решение.

<™>-E(S),-

4. Найти <ДУДР> (пользуясь переменными V, Т).
Решение.

<ДКДР>= — Т.

5. Найти < AS AV > (пользуясь переменным V, Т).
Решение.

<Д5ДУ>=(^)_рГ.

6. Найти < AS AT > (пользуясь переменными К, 7").
Решение.

<ASAT >=7\

7. Найти средний квадрат флуктуационного отклонения вертикально вися-
щего математического маятника.

Решение. Пусть /—длина маятника, m—его масса, <р—угол отклонения от вертикали. Работа R_mln в данном случае есть просто механическая работа против силы тяжести при отклонении маятника; для малых ф: R_ta\_n = ¹/₂ mg-lq?. Отсюда

Т

mgl

8. Найти средний квадрат флуктуационного отклонения точек натянутой
струны.

Решение. Пусть I—длина струны, F—сила ее натяжения. Рассмотрим точку, находящуюся на расстоянии х от одного из концов струны, и пусть у — ее поперечное смещение. Для определения <i/²> мы должны рассмотреть равно­весную форму струны при заданном смещении у точки х; она состоит из двух прямых отрезков, проведенных из точек закрепления струны в точку х, у. Работа, затрачиваемая при такой деформации струны, равна

ГУ² (1, I

2 V* ¹ I—х,

R*4n = F(V* + y^t-x) + F[V(1-х)* + У*-(1-х)\ ~ Ц-

Отсюда находим для среднего квадрата

< у^гУ—щХ (I—х).

9. Определить среднее значение произведения флуктуационных смещений двух различных точек струны.

Решение. Пусть y_lt у₂ — поперечные смещения точек, находящихся на расстояниях х_ъ х₂ от одного из концов струны (причем х_г > х_х). Равновесная форма при заданных у_г и у₂ составляется из трех прямых отрезков, и работа

D —^F(² *2 | 2 l—Xl „ 1 \

/?mi„-_T ^ _Xl{Xt-_Xj+y (Т=^^~ ^W2(V=^)j •

По формуле (111,8) найдем

Т

§ 113. Флуктуации в идеальном газе

Средний квадрат флуктуации числа частиц обычного идеаль­ного газа, находящихся в некотором выделенном в газе относи­тельно малом объеме, мы найдем, подставив в формулу (112,13) V=NT/P. Это дает следующий простой результат:

<(ДЛ0²> = ЛГ. (113,1)

Относительная флуктуация числа частиц равна, следовательно, просто обратному квадратному корню из среднего числа частиц:

< (AN²) >^1/2 _ 1
N '

Для того чтобы вычислить флуктуацию числа частиц в иде­альном газе Бозе или Ферми, следует воспользоваться формулой (112,14), подставив в нее выражение (56,5) для N как функции от fi, Т, V, получаемое интегрированием соответствующей функ­ции распределения. Мы не станем выписывать здесь получаю­щиеся таким способом довольно громоздкие выражения. Отметим лишь следующее обстоятельство. Мы видели, что у бозе-газа при температурах Т < Г₀ (см. § 62) давление не зависит от объема; другими словами, его сжимаемость обращается в бесконечность. Согласно формуле (112,13) отсюда следовало бы, что флуктуа­ции числа частиц тоже становятся бесконечными. Это означает, что при вычислении флуктуации в бозе-газе при низких темпе­ратурах нельзя пренебрегать взаимодействием его частиц, сколь бы слабым оно ни было; учет этого взаимодействия, которое должно существовать во всяком реальном газе, привел бы к ко­нечным флуктуациям.

Далее рассмотрим флуктуации в распределении частиц газа по различным квантовым состояниям. Введем снова в рассмотре-

ние квантовые состояния частиц (включая в это понятие также и различные состояния их поступательного движения), и пусть n_k — их числа заполнения.

Рассмотрим совокупность n_k частиц, находящихся в k-м кван­товом состоянии; ввиду полной статистической независимости этой системы частиц от остальных частиц газа (ср. § 37) можно применить к ней формулу (112,14):

<(An_k)*> = T^. (113,2)

В применении к ферми-газу надо подставить сюда

Произведя дифференцирование, найдем

((An_ky> = n~_k(\-n_k). (113,3)
Аналогичным образом найдем для бозе-газа

<(An_k)*> = n_k(l+n_k). (П3,4)

Для больцмановского газа при подстановке «_А = ехр[(р—е_А)/Г] получается, естественно, формула

<(An_k)*>=~n_k, (113,5)

в которую переходят как (113,3), так и (113,4) при п_А<^1.

Просуммируем формулу (113,3) или (113,4) по группе из Gj близких друг к другу состояний, содержащих всего N_J = '£_in_k частиц. В силу упомянутой уже статистической независимости флуктуации различных n_k получим

< (AN,.)* > = GjtTj (1 =f~rij) = #_у (I =F -^-), (113,6)

где «у—общее значение близких друг к другу n_k, a Nj — n~jGj.

Полученные формулы можно применить, в частности, к чер­ному излучению (равновесный бозе-газ фотонов), для чего надо положить в (113,4) р = 0. Рассмотрим совокупность квантовых состояний фотонов (в объеме V) с близкими значениями частот, лежащими в малом интервале Асо,-; число таких состояний равно Gj = Vu))A(uj/n²c³ (см. (63,3)). Общая энергия квантов в этом интервале частот есть£_Д(^== Л^Лсо,. Умножив формулу (113,6) на (hwj)² и опуская индекс /, получим следующее выражение для флуктуации энергии Е^_а черного излучения в заданном интер­вале частот Дсо (впервые найденное Эйнштейном, 1909):

<(АЕ^)*> = 1ш.Еь_а,+ ■ ОВД

Задача

Определить <(ДЛ!)²> для электронного газа при температурах, малых по сравнению с температурой вырождения.

Решение. При вычислении (dN/d\i)_{T v} можно пользоваться выражением (57,3) для р. при абсолютном нуле. Простое вычисление дает

§114. Формула Пуассона

Зная средний квадрат флуктуации числа частиц в заданном объеме газа (113,1), можно написать соответствующее гауссово распределение вероятностей флуктуации этого числа:

B»(^)dJV = ^=Wexp{--fc^4 -dN. (П4,1)

Эта формула, однако, применима лишь для малых флуктуации — отклонение N—N должно быть малым по сравнению с самим числом Л'.

Если выделенный в газе объем V достаточно мал, то число частиц в нем невелико, и представляет интерес рассмотрение также и больших флуктуации, при которых N — N становится сравнимым с N. Заметим, что этот вопрос имеет смысл лишь в применении к больцмановскому газу, так как в газах Ферми или Бозе вероятность таких флуктуации может стать заметной лишь в настолько малых объемах, что существенными становятся квантовые флуктуации.

Решение поставленного вопроса проще всего получить следую­щим образом. Пусть К₀ и N₀— полный объем газа и число частиц в нем, а V—малая по сравнению с V₀ часть объема. В силу однородности газа очевидно, что вероятность некоторой опреде­ленной частице находиться в объеме V равна просто отношению V/V₀, а вероятность одновременного нахождения в нем N опре­деленных частиц равна (V/V₀)^N. Аналогично вероятность частице не находится в объеме V равна (V₀—V)/V₀, а такая же вероят­ность одновременно для N₀— N определенных частиц есть (1—V/V₀)^N«-^N. Поэтому вероятность w_N того, что в объеме V будет находиться всего N каких-либо молекул, дается выражением

^W» = NHN.-N)l [TJ {^l-Tj ' (¹¹⁴'²⁾

где введен множитель, определяющий число возможных спосо­бов выбора Af из Л^о частиц.

В интересующем нас случае V<^.V₀, а число N хотя и мо­жет значительно отличаться от своего среднего значения N, но, разумеется, предполагается малым по сравнению с полным чи­слом N₀ частиц в газе. Тогда можно положить N₀!«(Af„—N)]Ntf и пренебречь N в показателе степени, так что получается

1 {N₀V\n{, V\n„

Но N_aV/V₀ есть не что иное, как среднее значение N числа частиц в объеме V. Поэтому имеем

Наконец, имея в виду известную формулу

11т (\ — -)" = е-^х,

заменяем (1—N/N₀)^N° с большим Л/„ на ехр (—N) и получаем окончательно искомое распределение вероятностей в виде¹)

N^Nexp(—N).... _оч

^Wn= ж— • (¹¹⁴>³)

Это — так называемая формула Пуассона. Легко убедиться в том,

что она удовлетворяет условию нормировки 2 &W=1.

jv=o

Вычислим с помощью этого распределения средний квадрат флуктуации числа частиц. Пишем:

оо оо Т"ЛГ

<ЛГ2>= 2 iV^ = exp(—~N) 2 ^N

= exp(— N)

V "^N ■ V ^W 1 a7». VT

Отсюда находим для искомой флуктуации прежнее значение

<(ДЛ/)²> = <Л/²> — W = N. (114,4)

!) Для малых флуктуации (| N—N | <^ N, N велико) эта формула перехо­дит, естественно, в формулу (114,1). В этом легко убедиться, воспользовав­шись асимптотической формулой Стирлинга для факториала большого числа Л': ЛП = УШ?.Ы" ехр (— N), и разложив lnw_N „ _{ряд по} степеням N — N.

Таким^ образом, средний квадрат флуктуации числа частиц ра­вен Njie только при больших, но и вообще при любых значе­ниях N.

Отметим, что формула (114,3) может быть получена и непо­средственно из распределения Гиббса. Согласно последнему рас­пределение N частиц газа, рассматриваемых одновременно, по различным квантовым состояниям определяется выражением

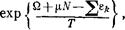
где 2 ^е* ^{есть с}У^мма энергий отдельных частиц. Для получения искомой вероятности w_N надо просуммировать это выражение по всем состояниям частиц, приходящимся на заданный объем V. Производя суммирование по состояниям каждой частицы неза­висимо, мы должны одновременно разделить результат на N1 (ср. § 41), так что получается

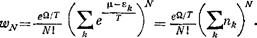
Но стоящая здесь сумма есть не что иное, как среднее значение N числа частиц в рассматриваемом объеме. Поэтому находим: w_N— const -N^N/N\, после чего из условия нормировки находим const = ехр (—N)¹), приходя снова к формуле (114,3).

§ 115. Флуктуации в растворах

Флуктуации термодинамических величин в растворах могут быть вычислены тем же методом, с помощью которого были рас­смотрены в § 112 флуктуации в телах, состоящих из одинаковых частиц. Соответствующие вычисления значительно упрощаются, если заранее учесть следующие соображения.

Рассмотрим некоторую малую часть раствора, содержащую заданное число N молекул растворителя, и поставим себе целью вычислить среднюю флуктуацию числа п молекул растворенного вещества в этой части, или, что то же, флуктуацию концентра­ции c = n/N в ней. Мы должны рассмотреть для этого наиболее полное равновесие раствора, возможное при данном неравновес­ном значении п (ср. примечание на стр. 366). Задание концент­рации не мешает установлению равновесия между данной малой частью и остальным раствором по отношению к обмену энергией между ними и по отношению к изменению их объемов. Первое означает (см. § 9), что температура остается постоянной вдоль всего раствора, а второе означает то же самое для давления (§ 12). Таким образом, для вычисления среднего квадрата <(Ас)²>

^J) То есть Q=—PV=—NT—в соответствии с уравнением состояния идеального газа.

достаточно рассматривать флуктуации концентрации, происходя­щие при неизменных температуре и давлении.

Этот факт уже сам по себе означает, что флуктуации концентра­ции, с одной стороны, и флуктуации температуры и давле­ния—с другой, статистически независимы, другими словами¹),

<ЛГДс> = 0, <ДсДР> = 0. (115,1)

Минимальная работа, необходимая для изменения числа п на An при постоянных давлении и температуре, согласно (96,1) равна #ть ⁼ АФ—р'Дга, где р/— химический потенциал растворенного вещества. Разлагая ДФ по степеням An, имеем

так что

Подставляя это выражение в общую формулу (112,1) и сравни­вая с формулой распределения Гаусса (110,5), получим для иско­мого среднего квадрата флуктуации числа п

<(А»)^,>-тЬт. ("5,2)

дп) р,т

или, разделив на N², для среднего квадрата флуктуации кон­центрации

<<Д_С)*> =-Г. (115,3)

V дс Jp.t

Последний, как и следовало (ср. стр. 372), обратно пропорцио­нален количеству вещества (N) в данной малой части раствора. Для слабых растворов др//дп — Т/п, и формула (115,2) дает

<(Дя)²> = д. (115,4)

Обратим внимание на аналогию (которую и следовало ожидать) с формулой (113,1) для флуктуации числа частиц в идеальном газе.

^J) Более строго в этом можно убедиться способом, указанным в приме­чании на стр. 372. С помощью термодинамического соотношения dE=TdS—PdV-\-\x'dn (при N = const) переписываем формулу (96,1) в виде

dR_m\n = (Т-То) dS - (Р—Р₀) dV+ (и/ - (iS) dn.

Отсюда видно, что если выбрать в качестве величин х,- следующие: x_x = AS, лг_а = ДУ, х₃ = Ап, то термодинамически взаимными с ними будут: Xj^—AT/T, Х₂ = — АР/Т, Х₃ = Ац'/Т. Равенства (115,1) следуют тогда из <х₃Х₁у=0, <*₃Х₂> = 0.

§ 116. Пространственная корреляция флуктуации плотности

Утверждение, что в однородной изотропной среде (газ или жидкость) все положения частиц в пространстве равновероятны, относится к каждой отдельной частице при условии, что все остальные частицы могут занимать произвольные положения. Это утверждение, конечно, не противоречит тому, что между взаим­ным положением различных частиц должна существовать в силу их взаимодействия некоторая корреляция: если рассматривать, скажем, одновременно две частицы, то при заданном положе­нии одной различные положения другой будут неравноверо­ятными.

Обозначим посредством п (г) точную (флуктуирующую) плот­ность числа частиц; произведение ndV есть число частиц, нахо­дящихся (в данный момент времени) в элементе объема dV. Для характеристики корреляции между положениями частиц в двух точках пространства введем пространственную корреляционную функцию флуктуации плотности:

< Ап-l Ап₂у = п₁п₂— ft², (116,1)

где Ап — п—п, а индексы 1 и 2 отличают значения п (г) в двух точках пространства г_х и г₂. В однородной изотропной среде корреляционная функция зависит только от абсолютной вели­чины расстояния г = \г₂—г_х| между обеими точками. При г—»-оо флуктуации в точках r_t и г₂ становятся статистически неза­висимыми, так что корреляционная функция стремится к нулю.

Смысл введенной таким образом корреляционной функции полезно пояснить следующими рассуждениями. В силу беско­нечной малости объема dV в нем может находиться одновремен­но не более одной частицы; вероятность нахождения в нем сразу двух частиц есть бесконечно малая величина более высокого порядка. Поэтому среднее число частиц ndV есть в то же вре­мя вероятность частице находиться в элементе dV. Обозначим далее посредством nw₁₂(r)dV₂ вероятность частице находиться в элементе объема dV₂ при условии, что одна частица находится в элементе dV_t (w₁₂—► 1 при г—► оо). Из сказанного очевидно, что среднее значение

<я_х dV_x ■n₂dV₂y = n dV_x ■ п ш₁₂ dV₂.

Отсюда: <ft₁n₂> = w₁₂n^%. В этом равенстве, справедливом при г_гфт₂ нельзя, однако, перейти к пределу г₂—>г_г, так как при выводе не учтено, что если точки 1 и 2 совпадают, то частица, находящаяся в dV_lt тем самым находится и в dV₂. Легко ви­деть, что соотношение, учитывающее это обстоятельство, имеет

вид

<м₁и_а> = м²ге;₁2+"⁶(^г8—^ri)- 016,2)

Действительно, выделим некоторый малый объем АУ и, умно­жив (116,2) на dV_xdV₂, проинтегрируем по этому объему. Член n^aw₁₂ даст при этом малую величину второго порядка (пропор­циональную (АУ)²); член же с б-функцией даст величину пер­вого порядка п A V, как и должно быть, поскольку (с точностью до величин первого порядка) в малом объеме может находиться лишь 0 или 1 частица.

Член с б-функцией целесообразно выделить и из корреля­ционной функции (116,1), записав ее в виде

<Ап₁Дп₂> = гсб (г_г—rj + п v (г), (П6,3)

где

v(r) = «fcW-l]. (116,4)

Мы будем называть корреляционной функцией как исходную величину <Ал, Att₂>, так и функцию v(r)¹).

Проинтегрируем теперь равенство (116,3) по dV_x dV₂ по неко­торому конечному объему V. Введя полное число N частиц в этом объеме (так что nV=N), получим

<(AJV)²> = Л/ +п 11 v(r) аУ_х dV₂,

или, перейдя от интегрирования по dV_x dV₂ к интегрированию по координатам одной из частиц и по относительным координа­там г = г_а—r_lf

j-_vdy₌ <m-^i. (116,5)

Таким образом, интеграл от корреляционной функции по неко­торому объему выражается через средний квадрат флуктуации полного числа частиц в этом объеме. Воспользовавшись для последнего термодинамической формулой (112,13), можно выра­зить этот интеграл через термодинамические величины:

3K£)-i. (над

В обычном (классическом) идеальном газе интеграл обра­щается в нуль, как и должно быть: в таком газе никакой кор­реляции между положениями различных частиц нет, поскольку

^г) Функция v (г) отличается от введенной в § 79 функции а>₁₂ (г) нормиров­кой: /j(b₁₂ = v.

384 флуктуации [гл. хп

между ними нет никакого взаимодействия — ни прямого, ни (как в квантовом идеальном газе) обменного.

Напротив, в жидкости (вдали от критической точки) первый член в выражении (116,6) мал по сравнению с единицей в силу малой сжимаемости жидкости, так что интеграл близок к—1¹). Основные силы взаимодействия между частицами жидкости имеют радиус действия порядка молекулярных размеров а. С учетом этих сил корреляционная функция \(г) убывает с расстоянием по экспоненциальному закону с показателем^—г /а²).

Поскольку флуктуации плотности и температуры статистиче­ски независимы, то при рассмотрении флуктуации плотности температуру можно считать постоянной. Постоянен по определе­нию также и полный объем тела. В таких условиях минималь­ная работа, требуемая для вывода тела из состояния равновесия, равна изменению AF_n его полной свободной энергии. Поэтому вероятность флуктуации

шел ехр(—ф¹). (П6.7)

Изменение AF„, связанное с флуктуациями плотности, может быть представлено в виде

A/^r„ = -₂-j^>j^>9(r)A«₁An₂dF₁dF₂. (116,8)

Покажем, каким образом корреляционная функция v(r) может быть найдена по функции q> (г)⁸).

Рассматривая тело большого, но конечного объема V, разло­жим Дя в ряд Фурье:

Дп = £Дп_ке'^кг, Дпк= Y^Ane-^ikrdV (116,9)

(причем ввиду вещественности Дя:Дя_к — Ant). При подста­новке этих выражений в (116,8) и интегрировании, все члены с произведениями Длк Апк-е¹<^к+к'>^г, к'Ф—к обращаются в нуль, и в результате находим

^д/гп=4£|Д"к|²<р(*), (116,10)

*) Значение—1 отвечает как бы взаимной непроницаемости частиц жидко­сти, рассматриваемых как плотно упакованные твердые шарики. ²)Существуют, однако, также и слабые, но более дальнодействующие (ван-дер-ваальсовы) силы взаимодействия. Эти силы приводят к появлению в корреляционной функции члена более медленно (по степенному закону) спа- дающего с расстоянием (см. том IX). ³) По математической терминологии ф(г) — вторая вариационная производ- ная от Д F_a по п (г).

к

где той же буквой ц> с указанием нового аргумента k обозна­чена компонента разложения функции ф (г) в интеграл Фурье:

Ф(*)= ^(f(r)e-^ikrdV. (П6,П)

Поскольку каждый из членов суммы (116,10) зависит только от одного из An_k) то флуктуации различных Ап_к статистически независимы. Каждый квадрат |Ди_к|² входит в сумму дважды (±к), так что распределение вероятностей его флуктуации да­ется выражением

tiyoiexpj— jrq>(k)\ An_k|² j.

Наконец, имея в виду, что |Дя_к|² есть сумма квадратов двух независимых величин (Дп_к комплексно), найдем отсюда для сред­него квадрата флуктуации

<l^A»H^e>=7?W- ⁽¹¹⁶'¹²>

С другой стороны, умножив равенство (116,3) с обеих сторон на ехр (— гкг) = ехр[—ik(r₂—rj] и снова проинтегрировав по аУ^аУъ, получим

<| Ая_к|²>=-£

l+v(*)1, v(£) = J v(r)e-^dV. (116,13)

Наконец, подставив сюда (116,12), приходим к искомому ре­зультату:

v(*) = =I--l. (116,14)

гщ (k)

Задача

Определить первый член разложения корреляционной функции разрежен­ного газа по степеням N/V.

Решение. Исходим из формулы (79,2). В первом приближении можно считать, что все остальные частицы, кроме двух заданных, находятся вдали друг от друга и их взаимодействием можно пренебречь, так что интегрирова­ния дают V^N~². С той же точностью можно положить /^, = /⁷_ид. В результате находим

v(r) = n[_e-^u^^r-l],

где U (г)—энергия взаимодействия двух частиц газа.

Отметим, что подстановка этого выражения в (79,1) дает для энергии газа

Этот результат находится, конечно, в соответствии с формулами (74,4—5) для свободной энергии слабо неидеального газа.

§ 117. Корреляция флуктуации плотности в вырожденном газе

Как уже было отмечено в предыдущем параграфе, в класси­ческом идеальном газе никакой корреляции между положениями различных частиц вообще нет. В квантовой механике, однако, такая корреляция возникает ввиду косвенного взаимодействия частиц идеального газа в силу принципа симметрии волновых функций

Дата добавления: 2014-11-07