Функции нескольких переменных

Дифференциальное исчисление.

Конец примера.

Конец примера.

Конец доказательства.

Пример 18.2. Вычислить производную сложной функции .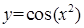

.

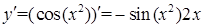Теорема 18.6. (Дифференцируемость обратной функции). Пусть 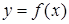строго монотонная и непрерывная на интервале I функция, принимающая значения из интервала E. Тогда, если 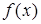дифференцируема на I, то на интервале E существует дифференцируемая обратная функция , причем

.

Доказательство. Из условий теоремы следует существование и единственность обратной функции , определенной на интервале E.

Тогда

.

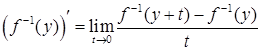Обозначим через h разность 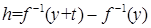, тогда, учитывая, что 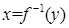, получим 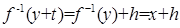, или 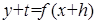. Отсюда, учитывая, что при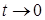 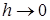, получим

Конец доказательства.

Пример 18.3.

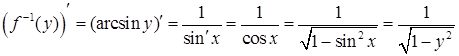
О. Если каждой паре чисел из некоторого множества D по некоторому закону соответствует значение Z из множества M, то переменная Z называется функцией двух переменных.

Переменная x и y – независимые переменные (аргументы).

z – зависимая переменная (функция)

z – f(x;y)

z – z(x;y)

Z – F(x;)

Функция двух переменных может быть задана:

1) графически

2) таблицей

3) формулами.

D(z) – область определения функции.

О. Часть плоскости XOY, ограниченная замкнутой кривой, причём точки этой кривой (границы области) могут принадлежать или не принадлежать D(z). y

Пример: 2

z =

4 - x² – y² ≥ 0

x² + y² ≤ 4 -2 0 2 x

x² + y² = 4

-2

z

0 2 y

x

Область определения функции z=f(x;y) представляет собой геометрическое место точек, расположенных в плоскости XOY. График же самой функции представляет собой поверхность, расположенную в пространстве.

Частные производные:

Рассмотрим функцию z = f(x;y) в некоторой области, зафиксируем произвольную точку M(x;y) и дадим x приращение ∆x, оставляя y неизменным.

При этом функция z получит приращение:

∆_x z = f(x + ∆x;y) – f(x;y) – частное приращение функции по аргументу x.

О. Частной производной от функции z = f(x;y) по независимой переменной x называется производная:

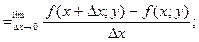
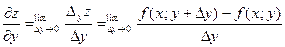
Частные производные функции нескольких переменных определяются, как производные этой функции по одной из них при условии, что остальные переменные считаются постоянными. Для частных производных справедливы обычные правила и формулы дифференцирования.

Например:

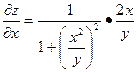
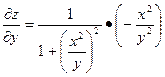
Дата добавления: 2014-10-22