
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дискретной случайной величины
|
|
|
|
Формы закона распределения
I. Табличная форма: в таблице перечислены все возможные значения дискретной случайной величины (в порядке возрастания) и соответствующие им вероятности:
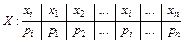
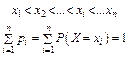
Опр.: Табличная форма закона распределения дискретной случайной величины называется рядом распределения ДСВ.
Задача 5.1: Вероятности сдать с первого раза семестровые экзамены по математике и по физике студент оценивает как 0,7 и 0,4. Составить ряд распределения числа экзаменов, которые студент сдаст с первого раза.
Решение: Так как с первого раза можно либо не сдать ни одного экзамена, либо один из них, либо все два, то есть случайная величина  – число экзаменов, которые студент сдаст с первого раза, может принять одно из значений 0, 1 или 2.
– число экзаменов, которые студент сдаст с первого раза, может принять одно из значений 0, 1 или 2.
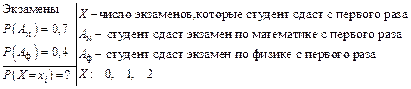
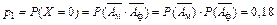
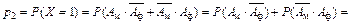
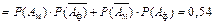
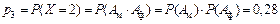
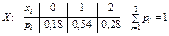
II. Графическая форма: в системе координат 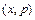 точки
точки 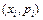 последовательно соединяются отрезками ломаной, из конечных точек которой опускаются перпендикуляры на ось
последовательно соединяются отрезками ломаной, из конечных точек которой опускаются перпендикуляры на ось 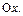
Опр.: Плоская фигура, ограниченная ломаной из последовательно соединенных отрезками точек 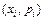 , прямыми
, прямыми 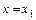 и
и 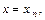 а также осью
а также осью 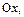 называется многоугольником распределения.
называется многоугольником распределения.
Задача 5.2: Используя условие задачи 5.1, построить многоугольник распределения числа экзаменов, которые студент сдаст с первого раза.
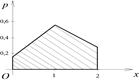 Решение:
Решение:
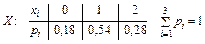
III. Аналитическая форма: закон распределения случайной величины может быть задан в виде формулы, связывающей 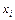 и
и 
Опр.: Если любому значению аргумента 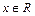 ставится в соответствие вероятность
ставится в соответствие вероятность 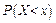 того, что случайная величина
того, что случайная величина  примет значение, меньшее заданного
примет значение, меньшее заданного 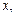 то говорят, что задана функция распределения случайной величины
то говорят, что задана функция распределения случайной величины 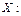
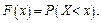
Замечание 1: Аргумент 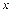 следует отличать от значения
следует отличать от значения  случайной величины
случайной величины  . Хотя в частном случае аргумент
. Хотя в частном случае аргумент 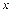 можно задать равным и значению
можно задать равным и значению 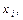 но вообще значения функции распределения можно определять для любого действительного значения аргумента.
но вообще значения функции распределения можно определять для любого действительного значения аргумента.
Замечание 2: Функция распределения – не единственный способ аналитического задания закона распределения. Существуют «стандартные» законы, для которых связь 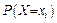 с
с 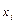 явно задается в виде формулы.
явно задается в виде формулы.
Замечание 3: График функции 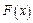 является еще одним способом графического задания закона распределения случайной величины.
является еще одним способом графического задания закона распределения случайной величины.
Свойства функции распределения:
1. 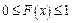 по определению.
по определению.
2. 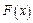 – неубывающая функция на всей числовой оси.
– неубывающая функция на всей числовой оси.
3. 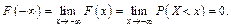

4. Вероятность попадания значений случайной величины в полусегмент 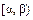 равна приращению функции распределения случайной величины на этом полусегменте:
равна приращению функции распределения случайной величины на этом полусегменте: 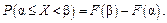
Задача 5.3: Найти функцию распределения и построить ее график для дискретной случайной величины из задачи 5.1. Вычислить вероятность 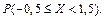
Решение: Будем искать значения функции по определению как вероятность для дискретной случайной величины  принять значение, меньшее заданного значения аргумента
принять значение, меньшее заданного значения аргумента 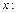
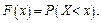
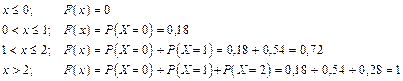
 – вероятность того, что
– вероятность того, что  примет значение меньше, чем самое малое из значений случайной величины, равна нулю, так как значений меньше
примет значение меньше, чем самое малое из значений случайной величины, равна нулю, так как значений меньше 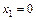 нет. Тем более
нет. Тем более 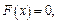 если выбрать значение аргумента еще меньшим, чем
если выбрать значение аргумента еще меньшим, чем 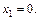 Таким образом, для любых заданных на промежутке
Таким образом, для любых заданных на промежутке 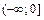 значений аргумента
значений аргумента 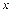 вероятность того, что
вероятность того, что  примет значение, меньшее
примет значение, меньшее 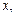 равна 0.
равна 0.
Если 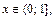 то вероятность для ДСВ
то вероятность для ДСВ  принять значение, меньшее заданного
принять значение, меньшее заданного 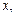 равна 0,18, так как такое событие возможно, только если ДСВ
равна 0,18, так как такое событие возможно, только если ДСВ  примет значение
примет значение 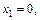 а это происходит с вероятностью
а это происходит с вероятностью 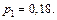 Таким образом, при
Таким образом, при 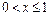
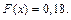
Для 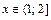 вероятность того, что ДСВ
вероятность того, что ДСВ  примет значение, меньшее заданного
примет значение, меньшее заданного 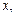 складывается из вероятностей двух несовместных событий:
складывается из вероятностей двух несовместных событий:  примет значение 0 с вероятностью 0,18 или значение 1 с вероятностью 0,54. Таким образом, при
примет значение 0 с вероятностью 0,18 или значение 1 с вероятностью 0,54. Таким образом, при 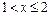
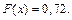
Рассмотрим 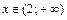 . Все значения ДСВ
. Все значения ДСВ  меньше значений аргумента
меньше значений аргумента 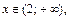 поэтому вероятность для ДСВ
поэтому вероятность для ДСВ  принять значение, меньшее заданного
принять значение, меньшее заданного 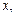 есть вероятность достоверного события и равна 1. Таким образом, при
есть вероятность достоверного события и равна 1. Таким образом, при 
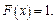
Обобщим результаты и построим график:
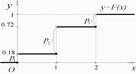
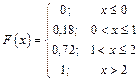
Вероятность попадания значений случайной величины в заданный промежуток найдем с помощью свойства 4:
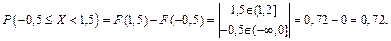
Замечание: Как видно на графике, функция распределения дискретной случайной величины имеет разрывы первого рода в точках 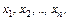 совпадающих со значениями случайной величины, причем скачки равны вероятностям
совпадающих со значениями случайной величины, причем скачки равны вероятностям 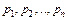 этих значений.
этих значений.
|
|
|
|
|
Дата добавления: 2014-10-23; Просмотров: 588; Нарушение авторских прав?; Мы поможем в написании вашей работы!