Для независимых повторных испытаний

Формула Пуассона

Алгоритм решения задач

на независимые повторные испытания:

1. Определить, в чем состоит опыт и каково число опытов .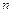

2. Определить, в чем состоит событие – результат единичного опыта, какова вероятность 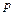наступления этого события и какова вероятность ненаступления этого события в единичном опыте.

3. Если требуется, найти наивероятнейшее число наступлений события 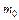из неравенства.

4. В зависимости от вопроса к задаче применить формулу Бернулли один или несколько раз.

При большом количестве опытов использование формулы Бернулли неудобно. Для этих случаев существуют приближенные (асимптотические) формулы.

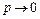Теорема 4.4: Если вероятность наступления события в каждом опыте при неограниченном увеличении числа опытов 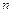, причем произведение стремится к постоянному числу , то вероятность того, что событие наступит 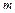раз в 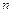независимых опытах, удовлетворяет предельному равенству

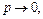Замечание 1: По схеме Бернулли , а в условии теоремы но с хорошей точностью справедлива приближенная формула Пуассона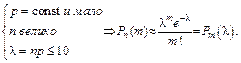

Замечание 2: Значения функции можно найти в специальной табл. (прил. I).

Замечание 3: По смыслу – среднее число наступлений события в 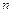независимых опытах.

Задача 4.5: Радиоаппаратура состоит из 2000 элементов. Вероятность отказа одного элемента в течение года равна 0,001. Какова вероятность отказа трех элементов за год? Какова вероятность отказа не менее двух элементов за год?

Решение: 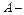элемент откажет в течение года.

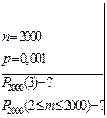Вероятность отказа трех элементов за год – это вероятность трех наступлений события в 2000 независимых опытах. Так как 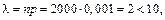то по формуле Пуассона 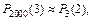это значение получим из табл. (прил. I). Оно находится в столбце значений функции при , в строке т. е.

Вероятность отказа не менее двух элементов за год – это вероятность двух, трех, четырех и т. д. наступлений события в 2000 независимых опытах. Найдем вероятность противоположного события: в течение года не откажет ни один элемент или только один элемент

Но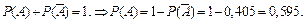

Ответ: а) б)

4.4. Формулы Муавра–Лапласа

Дата добавления: 2014-10-23