Теоремы умножения вероятностей

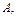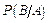Опр.: Вероятность события найденная при условии, что произошло событие называется условной вероятностью события и обозначается или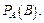

Замечание: Понятие условной вероятности вводится, чтобы установить, влияет ли на вероятность события изменение условий в виде наступления другого события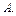

Опр.: События и называются независимыми, если вероятность любого из них не изменится от того, что произойдет другое. В противном случае и называются зависимыми.

Определение можно выразить с помощью формул:

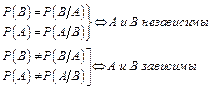
Задача 3.7: Из колоды в 52 листа извлекается одна карта. Рассматриваются события: – появление карты красной масти; – появление туза; 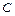– появление бубнового туза. Найти вероятности событий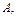 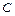и все возможные условные вероятности. Проверить попарную зависимость или независимость этих событий.

Решение:

, , .

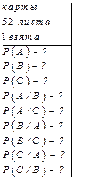
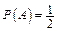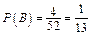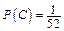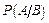– вероятность извлечь карту красной масти при условии, что вынут «туз»; «туза» можно вынуть 4 способами, среди них 2 карты красной масти, поэтому .

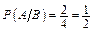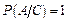– вероятность извлечь карту красной масти при условии, что вынут бубновый «туз» – вероятность достоверного события.

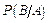– вероятность извлечь «туза» при условии, что вынута карта красной масти; красную карту можно извлечь 26 способами, среди них 2 способа взять «туза», поэтому .

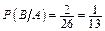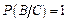– вероятность извлечь «туза» при условии, что вынут бубновый «туз»; очевидно, что это достоверное событие.

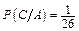– вероятность извлечь бубнового «туза» при условии, что вынута карта красной масти; красную карту можно вынуть 26 способами, а бубновый «туз» среди красных карт один.

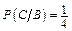– вероятность извлечь бубнового «туза» при условии, что вынут «туз»; «туза» из колоды можно взять 4 способами, и среди «тузов» бубновый один.

Таким образом, получили, что

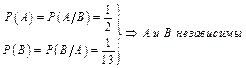
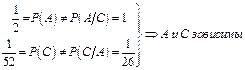
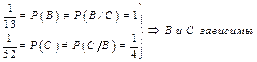
Замечание: Из примера легко видеть, что для выяснения зависимости или независимости событий и достаточно проверить лишь одно из равенств определения: 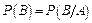или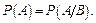

Теорема 3.3: Вероятность произведения зависимых событий и равна произведению вероятности события на вероятность события найденную при условии, что произошло событие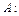

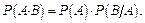
Замечание 1: События и в теореме можно поменять местами на основании свойства коммутативности умножения, тогда

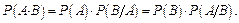
Задача 3.8: В урне 2 белых и 3 черных шара. Из урны вынимают подряд два шара. Найти вероятность того, что оба шара белые.

Решение:

Событие 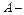появление двух белых шаров.

Событие 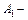появление белого шара при первом вынимании.

Событие 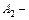появление белого шара при втором вынимании.

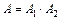. События и 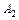зависимые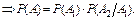

Один белый шар из пяти шаров, среди которых два белых, можно вытащить с вероятностью 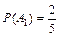. Второй белый шар среди оставшихся четырех шаров можно вытащить уже с вероятностью 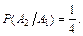Таким образом,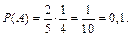

Ответ: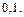

Теорема 3.4: Если события и независимы, то вероятность их произведения равна произведению вероятностей этих событий:

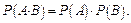
Замечание 1: Теоремы 3.3 и 3.4 можно распространить на любое конечное число событий.

Замечание 2: Теоремы дают возможность проверять зависимость событий еще одним способом:

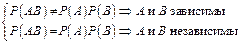
Задача 3.9: Найти вероятность совместного появления «герба» при одном бросании двух монет.

Решение:

Событие 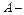появление «герба» на первой монете, .

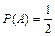Событие 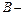появление «герба» на второй монете, .

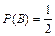События и независимые .

Ответ: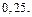

Дата добавления: 2014-10-23