Алгоритм решения задач с помощью теорем сложения

и умножения вероятностей:

1. Осмыслить условие задачи и записать краткое условие.

2. Ввести «сложное» событие 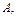вероятность которого нужно найти, и «простые» события, вероятности которых либо известны из условия, либо легко вычисляются.

3. Представить «сложное» событие в виде результата операций над «простыми» событиями.

4. Вероятность «сложного» события заменить вероятностью составленного из «простых».

5. Сначала применить одну из теорем сложения (для совместных или несовместных событий), затем – одну из теорем умножения (для зависимых или независимых событий).

6. Окончательная формула должна состоять из вероятностей «простых» событий, которые известны либо легко вычисляются.

Задача 3.10: Вероятность попадания в цель при стрельбе первого и второго орудий соответственно равны 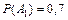и 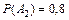. Найти вероятность попадания в цель при одном залпе из двух орудий хотя бы одним из них.

Решение:

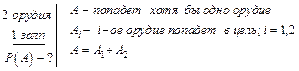
I способ: Событие состоится, если в цель попадет хотя бы одно орудие, то есть произойдет хотя бы одно из событий и 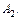По определению суммы событий 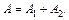События и 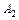совместны, так как оба орудия одновременно могут попасть в цель, и независимы, так как попадание первого орудия в цель не изменяет вероятности попадания в цель вторым орудием.

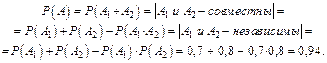
II способ: событие состоится, если совместно произойдут попадание в цель первого орудия – и непопадание в цель второго орудия – 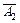(то есть по определению произведения событий 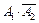), или непопадание в цель первого орудия – 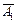и попадание в цель второго орудия – 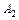(то есть 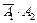), или, наконец, совместно попадут в цель оба орудия (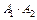). По определению суммы событий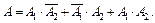

Тогда получим:

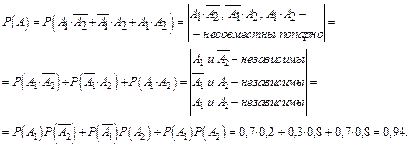
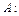
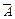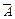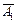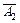III способ: Перейдем к событию, противоположному для– в цель не попадет ни одно орудие. Событие состоится, если произойдет и . По определению произведения событий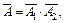

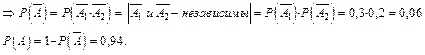
Ответ: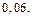

Вопросы для самоконтроля:

1. Чем отличаются классический, геометрический и статистический подходы к определению вероятности случайного события?

2. В каких единицах может измеряться мера благоприятной области при расчете вероятности по геометрическому определению?

3. Опыт состоит в извлечении одной карты из колоды в 36 карт. Рассматриваются события: – появление карты красной масти; – появление туза; 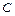– появление бубнового туза. Представить следующие исходы данного опыта в виде результатов операций над событиями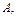 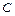(всеми или только некоторыми из них). 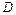– появление красного туза; 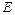– появление карты красной масти, не являющейся бубновым тузом; 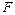– появление карты черной масти не являющейся тузом, 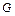– появление туза или карты красной масти.

4. В многоквартирном доме три подъезда с железными дверями. Ввести «простые события» и представить следующие «сложные» в виде результатов операций над «простыми». – все двери открыты; – все двери закрыты; 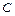– открыта только одна дверь; 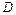– открыта только третья дверь; 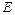– открыты две двери; 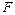– открыта хотя бы одна дверь.

5. Охарактеризуйте условия применения теорем сложения и произведения вероятностей.

Дата добавления: 2014-10-23