Для независимых повторных испытаний. Формула Пуассона применима при большом числе испытаний, если мало и

Формула Пуассона применима при большом числе испытаний, если мало и 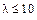. Но если последние условия не выполняются, то в случае большого числа испытаний, когда формула Бернулли не удобна, используют асимптотические формулы Муавра–Лапласа.

Теорема 4.5: Если вероятность наступления события в каждом опыте постоянна и отлична от 0 и 1, то вероятность того, что событие произойдет 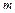раз в 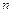независимых опытах при большом числе 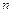, приближенно вычисляется по локальной формуле Муавра–Лапласа:

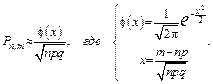
Замечание 1: Формула дает допустимую погрешность при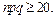

Замечание 2: Значения функции можно найти по табл. в Приложении II.

Замечание 3: Функция 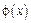четная, то есть 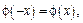поэтому в табл. (прил. II) приведены значения функции только для неотрицательных значений аргумента.

Замечание 4: С возрастанием аргумента функция 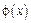монотонно убывает на неотрицательном промежутке, и поэтому можно считать, что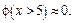

Задача 4.6: Найти вероятность того, что при 150 выстрелах мишень будет поражена ровно 70 раз, если вероятность попадания при одном выстреле равна 0,4.

Решение:

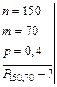
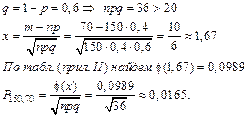
Ответ: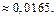

Теорема 4.6: Если вероятность наступления события в каждом из независимых опытов постоянна и отлична от 0 и 1, то вероятность наступления этого события не менее чем в и не более чем в 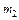опытах при достаточно большом числе испытаний 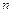приближенно вычисляется по интегральной формуле Муавра–Лапласа:

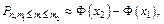где

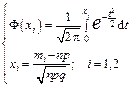
Замечание 1: Формула дает допустимую погрешность при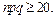

Замечание 2: Значения – функции Лапласа можно найти по табл. (прил. III).

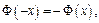Замечание 3: Функция – нечетная, то есть поэтому в табл. (прил. III) приведены значения функции только для неотрицательных значений аргумента.

Замечание 4: С возрастанием аргумента функция монотонно возрастает на неотрицательном промежутке, и поэтому можно считать, что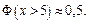

Замечание 5: Иногда в литературе под функцией Лапласа понимают также функцию 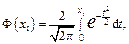тогда:

Задача 4.7: Игральную кость бросают 800 раз. Какова вероятность того, что число очков, кратное трем, выпадет не меньше 560 и не больше 274 раз?

Решение:

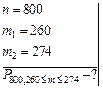
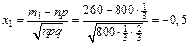
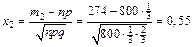
Ответ:

Теорема 4.7: Если вероятность наступления события в каждом из 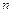независимых опытов постоянна и отлична от 0 и 1, то вероятность того, что относительная частота появления события по абсолютной величине отличается от вероятности наступления этого события в единичном опыте не более чем на величину , вычисляется по формуле:

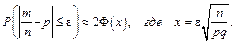
Задача 4.8: Вероятность появления события в каждом из 1000 независимых испытаний равна 0,75. Найти вероятность того, что относительная частота появления события отклонится от его вероятности по абсолютной величине не более чем на 0,001.

Решение:

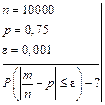
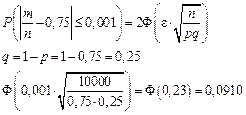
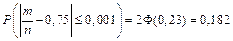
Это значит, что если провести достаточно большое количество опытов по 10000 испытаний в каждом, то примерно в 18,2 % этих опытов отклонение относительной частоты от постоянной вероятности 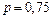по абсолютной величине не превосходит 0,001.

Ответ:

Задача 4.9: Вероятность появления события в каждом из независимых испытаний равна 0,2. Найти, какое отклонение относительной частоты появления события от его вероятности можно ожидать с вероятностью 0,9128 при 5000 испытаниях.

Решение:

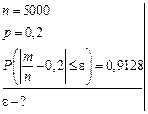
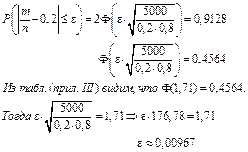
Ответ: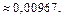

Задача 4.10: Сколько раз нужно подбросить монету, чтобы с вероятностью 0,996 можно было утверждать, что относительная частота выпадения «герба» отклонится от вероятности выпадения «герба» по абсолютной величине не более чем на 0,01?

Решение:

Чтобы у 996 экспериментаторов из 1000 статистическая вероятность выпадения «герба» получалась равной приближенно 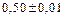, каждому из них нужно подбросить монету не менее 20736 раз.

Ответ: раз.

Вопросы для самоконтроля:

1. В чем отличие от ?

2. Охарактеризуйте условия применения формулы Бернулли и формулы Пуассона для независимых повторных испытаний.

3. Сформулируйте условия применения локальной и интегральной формул Муавра–Лапласа.

4. Укажите, какие из формул нахождения вероятности для независимых повторных испытаний целесообразно применить при решении следующей задачи.

Около 800 из 1000 студентов некоторого вуза обедают в пунктах питания учебного корпуса. Считая, что студенты не влияют друг на друга в своих предпочтениях, найти вероятность того, что среди случайно выбранных 100 студентов в пунктах питания учебного корпуса обедают: а) 75 из них; б) не менее чем 75 и не более чем 90; б) не менее чем 75; в) не более чем 74 студента.

5. Используя таблицы из Приложений, определите значения функций: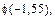

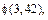
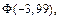
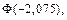
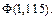
ЧАСТЬ II: СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

ЛЕКЦИИ №№ 5–6

Тема: ПОНЯТИЕ «СЛУЧАЙНАЯ ВЕЛИЧИНА».

Дата добавления: 2014-10-23