Случайные величины. Основные понятия

ВИДЫ СЛУЧАЙНЫХ ВЕЛИЧИН И ИХ ХАРАКТЕРИСТИКИ

План лекции:

1. Случайные величины. Основные понятия.

2. Формы закона распределения:

– табличная;

– графическая;

– математическая.

3. Математические операции над ДСВ.

4. Числовые характеристики ДСВ:

– математическое ожидание ДСВ;

– дисперсия ДСВ;

– среднее квадратическое отклонениеДСВ;

– мода ДСВ.

5. Моменты случайных величин:

– начальный момент порядка k СВ;

– центральный момент порядка k СВ.

6. Непрерывная случайная величина и ее функция распределения.

7. Плотность вероятности НСВ.

8. Числовые характеристики НСВ:

– математическое ожидание НСВ;

– дисперсия НСВ;

– мода НСВ;

– медиана НСВ.

Опр.: Случайная величина – это переменная, которая в результате опыта принимает одно из множества возможных значений, неизвестное заранее. Случайные величины будем обозначать заглавными латинскими буквами: Возможные значения случайной величины будем обозначать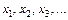

Примеры случайных величин:

Число детей, родившихся в г. Абакане в течение недели, 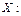0, 1, 2, …

Число выигрышных лотерейных билетов среди 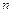купленных 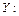0, 1, 2, ….

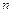Число выстрелов по мишени до первого попадания 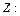0, 1, 2, …

Число выпадений «герба» в результате трех подбрасываний монеты 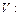0, 1, 2, 3.

Дальность полета снаряда может принять любое неотрицательное значение:

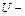расход электроэнергии потребителем за месяц,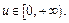

Ошибка измерения высоты может быть любого знака и величины, поэтому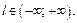

Если – время безотказной работы прибора, то, учитывая возможность отказа прибора в момент включения, следует добавить к положительным значениям этой случайной величины 0:

Среди рассмотренных выше примеров случайных величин первые четыре принимают значения, которые можно перечислить, а значения последних четырех пересчету не поддаются. По этому признаку случайные величины делятся на дискретные и непрерывные.

Опр.: Случайная величина называется дискретной, если ее значения можно перенумеровать (пересчитать).

Рассмотренные выше 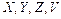– дискретные случайные величины.

Замечание: У дискретной случайной величины может быть конечное число значений (как у 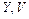), а может быть бесконечное, но обязательно счетное (как у ).

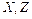Опр.: Случайная величина называется непрерывной, если она в результате опыта может принять любое из бесконечного множества действительных значений на некотором промежутке.

Рассмотренные выше 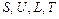– непрерывные случайные величины.

Одни значения случайная величина принимает чаще, другие – реже. Таким образом, любому из возможных значений 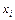можно поставить в соответствие некоторую вероятность появления этого значения Обозначение читается следующим образом: «– вероятность события 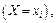состоящего в том, что случайная величина примет значение ».

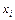Случайную величину можно полностью описать, если указать ее возможные значения и соответствующие им вероятности.

Опр.: Любое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями, называется законом распределения случайной величины.

Замечание: Сумма вероятностей всех возможных значений случайной величины равна единице как сумма вероятностей событий, составляющих полную группу. Таким образом, единица распределена между всеми значениями случайной величины, поэтому слово «распределение» входит в большинство понятий, относящихся к случайной величине.

Дата добавления: 2014-10-23