Формулы полной вероятности и Байеса. 1. Формулы полной вероятности и Байеса

ДЛЯ НЕЗАВИСИМЫХ ПОВТОРНЫХ ИСПЫТАНИЙ

ЛЕКЦИЯ № 4

Тема: ФОРМУЛЫ ВЕРОЯТНОСТИ СОБЫТИЙ

План лекции:

1. Формулы полной вероятности и Байеса.

2. Формула Бернулли для независимых повторных испытаний.

3. Формула Пуассона для независимых повторных испытаний.

4. Формулы Муавра–Лапласа для независимых повторных испытаний.

Встречаются случаи, в которых событие происходит только после того, как состоится одно из событий, составляющих полную группу, причем заранее неизвестно какое. Тем не менее, если известны условные вероятности события 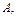то «безусловную» вероятность можно найти.

Задача 4.1: Среди 25 экзаменационных билетов 20 «трудных» и 5 «легких». Студент берет билет вторым по счету. Какова вероятность того, что ему достанется «легкий» билет?

Шансы выбрать «легкий» билет сдающего экзамен вторым по счету студента зависят от того, что досталось первому, поэтому они находятся в неравных условиях. Если первый взял «легкий» билет, то шансы второго уменьшились, а если «трудный», то возросли. Но обычно второй студент не знает, что досталось первому, значит, нужно учесть все возможности. В данной ситуации это нетрудно, так как предположений всего два.

В общем случае, если до опыта, в результате которого возможно наступление события 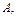должно произойти одно из событий полной группы 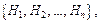то говорят, что пара таких последовательных опытов выполняется по схеме Байеса.

Теорема 4.1: Если событие может произойти только при условии наступления одного из событий (гипотез) 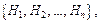составляющих полную группу, то вероятность события определяется формулой полной вероятности:

.

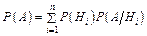Решение задачи 4.1:

Если вероятность события известна, то можно пересчитать вероятности гипотез при условии, что событие произошло, то есть найти …,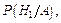

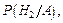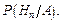
Ответ: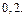

Теорема 4.2: Если выполняются условия теоремы 4.1, то вероятность гипотезы 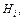найденная при условии наступления события 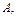определяется формулой Байеса:

.

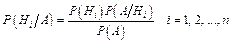Замечание: Следует четко различать вероятности событий в формулах данного параграфа:

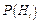– вероятность 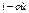гипотезы до наступления события (пока опыт не проводился);

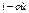– вероятность гипотезы после наступления события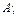

– вероятность наступления события при условии, что до опыта состоялась 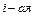гипотеза;

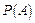– полная вероятность события с учетом всех возможных гипотез, если неизвестно, какая из них произошла перед наступлением события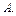

Задача 4.2: Используя условие задачи 4.1, найти вероятность того, что у первого студента был легкий билет, если второму достался легкий.

Решение:

Вопрос задачи относится к первому студенту, причем предлагается учесть, что досталось второму, то есть требуется найти вероятность гипотезы 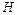при условии наступления события 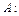это вероятность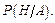

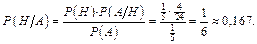
Ответ: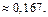

Алгоритм решения задач на применение схемы Байеса:

1. Осмыслить условие задачи и записать краткое условие. Сформулировать событие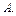

2. Сформулировать гипотезы 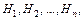которые составляют полную группу, а одна из них должна произойти до события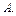

3. Найти вероятности гипотез 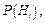которые записать в столбец и проверить выполнение условия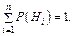

4. Рядом в столбец записать условные вероятности события при условии, что состоялась соответствующая гипотеза, то есть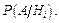

5. По формуле полной вероятности найти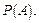

6. Если необходимо, найти вероятность гипотезы при условии, что произошло событие 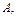то есть по формуле Байеса.

Дата добавления: 2014-10-23