Б.13. Пересечение прямой с плоскостью общего и частного положения. Определение видимости

Б.12. Линия пересечения 2 плоскостей (плоскости заданы не следами). Определение видимости.

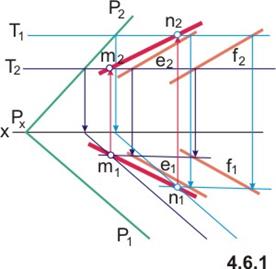Если же пересекающиеся плоскости (или одна из них) заданы не следами, то для построения линии пересечения их применяется метод вспомогательных секущих плоскостей. Сущность этого метода состоит в том, что обе заданные плоскости пересекаются третьей (обычно плоскостью частного положения - горизонтальной или фронтальной), затем строятся линии пересечения первой заданной плоскости с третьей, второй заданной с третьей. Там, где эти линии пересекаются, отмечается точка, общая для заданных плоскостей. Вторая общая точка находится при помощи еще одной вспомогательной плоскости. (Задача: На рис. 4.6.1 показано построение линий пересечения двух плоскостей, одна из которых задана следами, а вторая - параллельными прямыми. В качестве вспомогательных секущих плоскостей использованы горизонтальные плоскости Т₁ и Т₂.)

Для рассмотрения пересечения прямой и плоскости целесообразно начать с рассмотрения случая пересечения двух плоскостей (рис. 3.9), когда одна из пересекающихся плоскостей параллельна горизонтальной плоскости проекций (α | | π₁, f⁰_α | | Х). В этом случае линия пересечения а, принадлежащая плоскости α, будет также параллельна плоскости π₁, (рис. 3.9. а), т. е. будет совпадать с горизонталью пересекающихся плоскостей (а ≡ h).

а б в

Рис. 3.8. Прямые, параллельные плоскостям, заданным:
а - плоскостью треугольника АВС;
б - двумя пересекающимися прямыми а ∩ b;
в - горизонтальным h⁰_α и фронтальным f⁰_α следами

Если одна из плоскостей параллельна фронтальной плоскости проекций (рис. 3.9. б), то линия пересечения а, принадлежащая этой плоскости, будет параллельна плоскости π₂ и будет совпадать с фронталью пересекающихся плоскостей (а ≡ f).

Пример построения точки пересечения (К) прямой а (АВ) с плоскостью α (DEF) показан на рис. 3.10. Для этого прямая а заключена в произвольную плоскость β и определена линия пересечения плоскостей α и β.

В рассматриваемом примере прямые АВ и MN принадлежат одной плоскости β и пересекаются в точке К, а так как прямая MN принадлежит заданной плоскости α (DEF), то точка К является и точкой пересечения прямой а (АВ) с плоскостью α. (рис. 3. 11).

Для решения подобной задачи на комплексном чертеже необходимо уметь находить точку пересечения прямой общего положения с плоскостью общего положения.

а б

Рис. 3.9. Частный случай пересечения плоскости общего положения с плоскостями: а - горизонтального уровня; б - фронтального уровня

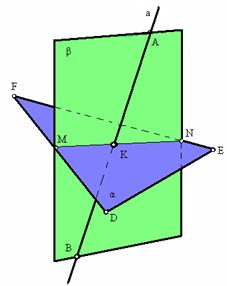Рис. 3. 10. Построение точки пересечения прямой с плоскостью

Рассмотрим пример нахождения точки пересечения прямой АВ c плоскостью треугольника DEF представленный на комплексном чертеже (рис. 3.11).

Для нахождения указанной точки пересечения через фронтальную проекцию прямой А₂В₂ проведена фронтально проецирующая плоскость β которая пересекла треугольник по прямой MN. На фронтальной плоскости проекций (π₂) эта прямая представлена проекциями двух точек M₂, N₂. Из условия принадлежности прямой плоскости на горизонтальной плоскости проекций (π₁) находятся горизонтальные проекции полученных точек M₁ N₁. В пересечении горизонтальных проекций прямых А₁В₁ и M₁N₁ образуется горизонтальная проекция точки их пересечения (К₁). По линии связи и условиям принадлежности на фронтальной плоскости проекций находится фронтальная проекция точки пересечения (К₂).

Видимость отрезка АВ относительно треугольника DEF определена методом конкурирующих точек.

На плоскости π₂ рассмотрены две точки N ∈ EF и 1∈ AB. По горизонтальным проекциям этих точек можно установить, что точка N расположена ближе к наблюдателю (Y_N>Y₁), чем точка 1 (направление луча зрения параллельно S). Следовательно, прямая АВ, т. е. часть прямой АВ (К₁) закрыта плоскостью DEF на плоско

Дата добавления: 2014-11-06