Дифференциальные уравнения движения материальной точки в проекциях на оси естественного трехгранника

Пусть точка М массы m движется по заданной гладкой кривой, лежащей в одной плоскости 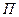(рисунок 3.2).

Рис. 3.2

Выберем на кривой начало отсчета 0, и будем определять положение точки М координатой . Поместим начало отсчета подвижных осей естественного трехгранника Min в точке M, где ось Mi направлена по касательной к траектории в сторону положительного отсчета координаты S; ось Mn – по нормам к траектории, лежащей в плоскости П и направленной в сторону вогнутости траектории: ось Mb (b - бинормаль) – перпендикулярна к первым двум так, чтобы она образовала с ними первую систему осей.

По аксиоме связей из статики, данную точку сделаем свободной, заменив связь ее реакцией

Запишем для данной точки основное уравнение динамики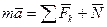

Проецируя это равенство на оси естественного трехгранника, учитывая, что вектор ускорения 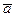расположен в плоскости П, а , получим:

, ,

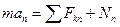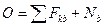
Так как 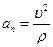, , то дифференциальные уравнения движения точки будут:

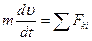
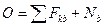
(3.6)

Если точка M будет свободной, то и дифференциальные уравнения движения будут:

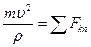
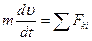
(3.7)

Дата добавления: 2014-11-25