Определение скоростей точек плоской фигуры с помощью мгновенного центра скоростей

Другой простой и наглядный метод определения скоростей точек плоской фигуры (или тела при плоском движении) основан на понятии о мгновенном центре скоростей.

Мгновенным центром скоростей (МЦС) называется точка плоской фигуры, скорость которой в данный момент времени равна нулю.

Если фигура движется непоступательно, то такая точка в каждый момент времени t существует и притом единственная. Пусть в момент времени t точки А и В плоскости фигуры имеют скорости и , непараллельные друг другу (рис. 2.21.). Тогда точка Р, лежащая на пересечении перпендикуляров Аа к вектору и Вb к вектору , и будет мгновенным центром скоростей, так как .

Рисунок 2.21

В самом деле, если , то по теореме о проекциях скоростей вектор должен быть одновременно перпендикулярен и АР (так как ), и ВР (так как ), что невозможно. Из этой же теоремы видно, что никакая другая точка фигуры в этот момент времени не может иметь скорость, равную нулю.

Если теперь в момент времени t взять точку Р за полюс. То скорость точки А будет

,

(2.52)

так как =0. такой же получается для любой другой точки фигуры. Тогда, скорости точек плоской фигуры определяются в данный момент времени так, как если бы движение фигуры было вращением вокруг мгновенного центра скоростей. При этом

(); ()

(2.53)

и так для любой точки фигуры.

Из этого следует еще, что и , тогда

= ,

(2.54)

т.е. что скорости точек плоской фигуры пропорциональны их расстоянию от мгновенного центра скоростей.

Полученные результаты приводят к следующим выводам:

1. Для определения мгновенного центра скоростей надо знать только направления скоростей, например, и каких-нибудь двух точек А и В плоской фигуры.

2. Для определения скорости любой точки плоской фигуры надо знать модуль и направление скорости какой-нибудь одной точки А фигуры и направление скорости другой её точки В.

3. Угловая скорость 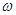плоской фигуры равна в каждой момент времени отношению скорости какой-нибудь точки фигуры к её расстоянию от мгновенного центра скоростей Р:

.

(2.55)

Найдем, еще другое выражение для ω из равенств 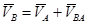и следует, что и , откуда

.

(2.56)

Рассмотрим некоторые частные случаи определения МЦС, которые помогут решать теоретической механики.

1. Если плоскопараллельное движение осуществляется путем качения без скольжения одного цилиндрического тела по поверхности другого неподвижного, то точка Р катящегося тела, касающаяся неподвижной поверхности (рис. 2.22), имеет в данный момент времени вследствие отсутствия скольжения скорость, равную нулю (), и следовательно, является мгновенным центром скоростей.

Рисунок 2.22

2. Если скорости точек А и В плоской фигуры параллельны друг другу, причем линия АВ не перпендикулярна (рис.2.23,а), то мгновенный центр скоростей лежит в бесконечности и скорости всех точек // . При этом из теоремы о проекциях скоростей следует, что , т.е. , в этом случае фигура имеет мгновенное поступательное движение.

3. Если скорости точек А и В плоской фигуры // друг другу и при этом линия АВ перпендикулярна , то мгновенный центр скоростей Р определяется построением (рис. 2.23,б).

Рисунок 2.23

Справедливость построений следует из . В этом случае, в отличие от предыдущих, для нахождения центра Р надо кроме направлений знать еще и модули скоростей и .

4. Если известны вектор скорости какой-нибудь точки В фигуры и её угловая скорость ω, то положение мгновенного центра скоростей Р, лежащего на перпендикуляре к (см. рис. 2.21), можно найти из равенства , которое дает .

Дата добавления: 2014-11-25