Уравнения плоскопараллельного движения. Разложение движения на поступательное и вращательное

Плоскопараллельное движение твердого тела

Плоскопараллельным (плоским) называется движение твердого тела, при котором траектории всех его точек лежат в плоскостях, параллельных некоторой неподвижной плоскости. Примеры плоского движения: плоское движение совершают многие части механизмов и машин, например, катящееся без скольжения колесо, шатун в кривошипно-ползунном механизме и др.

При таком движении все точки твердого тела, лежащие на перпендикуляре, восстановленном к этой плоскости, имеют одинаковые траектории, скорости и ускорения. Следовательно, при изучении плоского движения твердого тела достаточно исследовать движение плоской фигуры, являющейся сечением твердого тела плоскостью, параллельной неподвижной (рис. 2.15).

Рисунок 2.15

Положение фигуры S в плоскости Oxy (рис. 2.16) определяется положением какого-нибудь отрезка АВ. В свою очередь положение отрезка АВ можно определить, зная координаты , 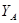точки А и угол φ, который АВ образует с осью Х. Точку А, выбранную для

Рисунок 2.16

определения положения фигуры S, будем называть полюсом. При движении фигуры , 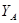и φ будут изменяться. Чтобы знать положение фигуры в плоскости Oxy надо знать

.

(2.47)

Эти уравнения, определяющие закон происходящего движения называются уравнениями движения плоской фигуры в её плоскости. Они же и есть уравнения плоскопараллельного движения твердого тела.

При φ=const первые два уравнения определяют поступательное движение, при котором все точки движутся также как и полюс А. При и 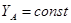движение фигуры определять третье уравнение, так как полюс А неподвижен. Это будет вращение фигуры вокруг полюса А.

Поэтому в общем случае движение плоской фигуры в её плоскости может рассматриваться как слагающееся из поступательного движения, при котором все точки фигуры движутся также, как полюс А, и из вращательного движения вокруг этого полюса.

Основными кинематическими характеристиками плоского движения являются скорость и ускорение поступательного движения, равные скорости и ускорению полюса , а также угловая скорость ω и угловое ускорение ε вращательного движения вокруг полюса.

Изучая плоское движение в качестве полюса можно выбирать любую точку фигуры. Рассмотрим, что получится, если вместо А выбрать в качестве полюса другую точку С и определить положение фигуры отрезком CD, образующим с осью Ох угол (рис. 2.17).

Рисунок 2.17

Характеристика поступательной части движения при этом изменится, так как в общем случае (иначе движение фигуры было бы поступательным). Характеристика же вращательной части движения, т.е. ω и ε, остаются неизменными. Действительно, проведя из С прямую // АВ, мы видим, что в любой момент времени угол а . Тогда или 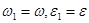. Следовательно, вращательная часть движения от выбора полюса не зависит.

Дата добавления: 2014-11-25