
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Угловая скорость и угловое ускорение тела
|
|
|
|
Величина, характеризующая быстроту изменения угла поворота φ с течением времени, называется угловой скоростью.
Если за промежуток времени 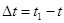 тело совершает поворот на угол
тело совершает поворот на угол 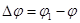 , то численно средней угловой скоростью тела за этот промежуток времени будет
, то численно средней угловой скоростью тела за этот промежуток времени будет  . В пределе при
. В пределе при 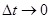 получим
получим
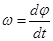 или или 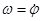 . .
| (2.32) |
Таким образом, числовое значение угловой скорости тела в данный момент времени равно первой производной от угла поворота по времени.
Правило знаков: когда вращение происходит против хода часовой стрелки, ω> 0, а когда по ходу часовой стрелки, то ω< 0.
В качестве единицы измерения обычно применяют 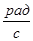 или, так как радиан – величина безразмерная,
или, так как радиан – величина безразмерная, 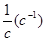 .
.
В теоретических выкладках удобнее пользоваться вектором угловой скорости 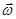 , модуль которого равен
, модуль которого равен 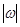 и который направлен вдоль оси вращения тела в ту сторону, откуда вращение видно против хода часовой стрелки. Этот вектор сразу определяет и модуль угловой скорости, и ось вращения, и направление вращения вокруг этой оси.
и который направлен вдоль оси вращения тела в ту сторону, откуда вращение видно против хода часовой стрелки. Этот вектор сразу определяет и модуль угловой скорости, и ось вращения, и направление вращения вокруг этой оси.
Величина, характеризующая быстроту изменения угловой скорости с течением времени, называется угловым ускорением тела.
Если за промежуток времени  приращение угловой скорости равно
приращение угловой скорости равно 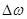 , то отношение
, то отношение 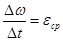 , т.е. определяет значение среднего ускорения вращающегося тела за время
, т.е. определяет значение среднего ускорения вращающегося тела за время  .
.
При стремлении 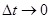 получаем величину углового ускорения в момент t:
получаем величину углового ускорения в момент t:
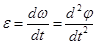 или или  . .
| (2.33) |
Таким образом, числовое значение углового ускорения тела в данный момент времени равно первой производной от угловой скорости или второй производной от угла поворота тела во времени.
В качестве единицы измерения обычно применяют  или, что тоже,
или, что тоже, 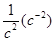 .
.
Если модуль угловой скорости со временем возрастает, вращение тела называется ускоренным, а если убывает, - замедленным. Когда величины ω и ε имеют одинаковые знаки, то вращение будет ускоренным, когда разные – замедленным.  По аналогии с угловой скоростью угловое ускорение также можно изобразить в виде вектора
По аналогии с угловой скоростью угловое ускорение также можно изобразить в виде вектора 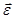 , направленного вдоль оси вращения. При этом
, направленного вдоль оси вращения. При этом
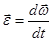 . .
| (2.34) |
Если тело вращается ускоренно направление 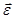 совпадает с
совпадает с 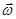 , и противоположно
, и противоположно 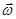 при замедленном вращении.
при замедленном вращении.
Если угловая скорость тела остается во время движения постоянной (ω=const), то вращение тела называется равномерным.
Из 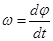 имеем
имеем 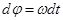 . Отсюда, считая, что в начальный момент времени
. Отсюда, считая, что в начальный момент времени 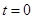 угол
угол  , и беря интегралы слева от
, и беря интегралы слева от 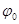 до
до 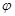 , а справа от 0 до t, получим окончательно
, а справа от 0 до t, получим окончательно
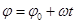 . .
| (2.35) |
При равномерном вращении, когда 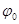 =0,
=0, 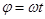 и
и 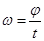 .
.
Скорость равномерного вращения часто определяют числом оборотов в минуту, обозначая эту величину через n об/мин. Найдем зависимость между n об/мин и ω 1/с. При одном обороте тело повернется на 2π, а при n оборотах на 2π n; этот поворот делается за 1 мин, т.е. t= 1мин=60с. Из этого следует, что
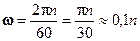 . .
| (2.36) |
Если угловое ускорение тела во все время движения остается постоянным (ε =const), то вращение называется равнопеременным.
В начальный момент времени t =0 угол  , а угловая скорость
, а угловая скорость 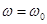 (
(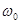 - начальная угловая скорость).
- начальная угловая скорость). 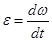 ;
;  =ε
=ε 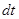 . Интегрируя левую часть от
. Интегрируя левую часть от 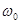 до
до 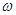 , а правую от 0 до t, найдем
, а правую от 0 до t, найдем
 . .
| (2.37) |
Если заменить 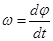 , то
, то 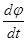 =
= 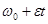 или
или  , вторично интегрируя, найдем закон равнопеременного вращения
, вторично интегрируя, найдем закон равнопеременного вращения
 . .
| (2.38) |
Угловая скорость ω этого вращения  . Если ω и ε имеют одинаковые знаки, вращение будет равноускоренным, а если разные – равнозамедленным.
. Если ω и ε имеют одинаковые знаки, вращение будет равноускоренным, а если разные – равнозамедленным.
|
|
|
|
|
Дата добавления: 2014-11-25; Просмотров: 1303; Нарушение авторских прав?; Мы поможем в написании вашей работы!