Теорема об изменении количества движения точки

Пусть точка М массы m движется под действием сил 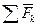(рисунок 3.1). Запишем для данной точки основное уравнение динамики (3.2)

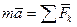
Так как 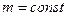, 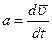то основное уравнение динамики запишется в виде:

(3.13)

Равенство (3.13) выражает теорему об изменении количества движения точки в дифференциальной форме: производная по времени от количества движения точки равна геометрической сумме всех действующих на точку сил.

Пусть в момент времени t=0 скорость точки , а в момент времени t скорость точки . Разделяя переменные в равенстве и интегрируя, получим:

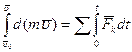
Так как 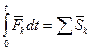, геометрической сумме импульсов сил 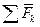, то

(3.14)

Равенство (3.14) выражает теорему об изменении количества движения точки в конечном виде: изменение количества движения точки за некоторый конечный промежуток времени равно геометрической сумме импульсов всех действующих на точку за тот же промежуток времени в проекциях на оси координат:

;

;

.

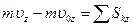Теорема об изменении количества движения точки в основном применяется на тех участках траектории движения точки, на которых задано время движения точки или это время нужно определить.

Момент количества движения точки относительно центра и оси. Теорема об изменении момента количества движения точки (теорема моментов)

В некоторых задачах в качестве динамической характеристики движения точки вместо самого вектора количества движения рассматривают его момент относительно некоторого центра или оси.

Рис. 3.4

Эти моменты определяются так же, как и моменты силы в статике.

Таким образом, моментом количества движения точки относительно некоторого центра О называется векторная величина 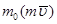, определяемая равенством:

(3.15)

где r – радиус – вектор движущейся точки М, проведенный из центра О. Вектор 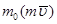направлен перпендикулярно плоскости, проходящей через вектор и центр О, а (рис. 3.4: для сравнения на нем показан и вектор , который перпендикулярен плоскости, проходящей через 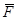и центр О)

Момент количества движения точки относительно какой-нибудь оси , проходящей через центр О, будет равен проекции вектора 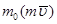на эту ось:

,

где 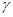– угол между вектором 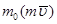и осью .

Теорема моментов устанавливает, как изменится со временем вектор 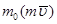. Для доказательства продифференцируем по времени равенство (3.15). Получим:

Но 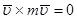как векторное произведение двух параллельных векторов, а

Следовательно, 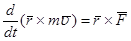или

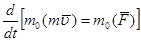
(3.16)

Равенство (3.16) выражает теорему моментов относительно центра: производная по времени от момента количества движения точки, взятого относительно какого-нибудь неподвижного центра равна моменту действующей на точку силы относительно того же центра.

Проецируя равенство (3.16) на какую-нибудь ось , проходящую через центр О, получим: .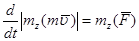

Равенство (3.5) выражает теорему моментов относительно оси

Из равенства (3.4) следует, что если , то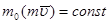

Дата добавления: 2014-11-25