Задачи динамики

1. Зная закон движения точки в выбранной системе отсчета, определить действующую на нее силу (первая задача динамики).

2. Зная действующую на точку силу и массу, определить закон движения точки (вторая задача динамики).

Несвободная материальная точка – это точка, связанная с другими материальными объектами.

Любую несвободную материальную точку можно рассматривать как свободную, отбросив связь и заменив ее действие реакцией этой связи.

Для несвободной материальной точки второй закон динамики:

, (1.7)

где – активные силы, действующие на точку;

– реактивные силы, действующие на точку.

Для решения первой задачи динамики из закона движения точки определяем ускорение, а потом силу, действующую на точку.

Задача 11 (26.12)

Кузов трамвая с колесами массой 11т. движется по прямолинейному горизонтальному участку совершая на рессорах колебания см (рис. 1.4).

Найти наибольшее и наименьшее давление на рельсы.

Решение

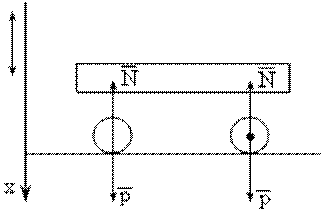
Рис. 1.4

Рассмотрим, какие силы действуют на колесо вагона:

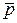– сила тяжести;

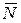– сила реакции опоры.

На рельс действует сила давления, равная по величине силе 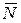и противоположно ей направлена. Так как вагон совершает колебания в вертикальной плоскости, то:

.

Выберем ось координат х в направлении колебаний вагона с началом в положении статического равновесия и спроектируем это векторное уравнение:

Движение вагона вниз		; или:
Движение вагона вверх

Отсюда следует, что:

, т.к. ,

см/с = -2 м/с, тогда:

Ответ: ; .

Задача 1.2 (26.14)

Тело, весом 20Н совершает колебательное движение по горизонтальной прямой м. Найти зависимость между силой Р, действующей на тело и расстояние S, а также наибольшую величину этой силы.

Решение

Составим дифференциальное уравнение движения тела (т.е. второй закон Ньютона):

.

Так как , то ; .

Тогда:

, или

.

Наибольшее значение силы будет тогда, когда , т.е.:

.

Ответ: ; .

Задача 1.3 (26.13)

Поршень двигателя внутреннего сгорания совершает горизонтальные колебания согласно закону см., где 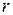– длина кривошипа, – длина шатуна, – постоянная по величине угловая скорость вала.

Определить наибольшее значение силы, действующей на поршень, если вес последнего Q.

Решение

Данная задача представляет собой вторую основную задачу, т.е. когда дан закон движения и необходимо определить силу, которая приводит к такому движению.

Запишем дифференциальное уравнение движения поршня, т.е. второй закон Ньютона:

.

Так как , то:

;

, тогда

.

Так как , максимальное значение силы будет тогда, когда и .

.

Ответ: .

Для решения второй (основной) задачи динамики необходимо выполнить следующие операции:

1. Составить дифференциальное уравнение движения:

а) выбрать начало отсчета и провести координатные оси. Если точка может находиться в положении равновесия, то начало отсчета помещается в положение статического равновесия. Направление оси, обычно, соответствует направлению движения точки;

б) изобразить движущуюся точку в произвольном положении, но так, чтобы и ;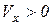

в) подсчитать сумму проекций всех сил на координатную ось.

2. Проинтегрировать дифференциальное уравнение.

3. Определить постоянные интегрирования (определение постоянных интегрирования производится по начальным условиям).

Наиболее распространены случаи, когда сила зависит от времени, от расстояния или от скорости движения точки:

.

Возможны также их линейные сочетания.

Задача 1.4

Точка, массой m совершает прямолинейное движение под действием силы , где и постоянные величины. В начальный момент скорость равна . Найти уравнение движения.

Решение

По 2 ^ому закону Ньютона: , или .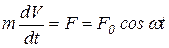

; , отсюда:

; .

Так как , то , отсюда

,

,

.

Вопросы для самоконтроля:

1. Задачи динамики?

2. Законы динамики?

3. Что такое сила тяжести и вес тела?

Задачи, рекомендуемые для самостоятельного решения: 26.1. – 26.36. [3].

Литература: [1] – [5].

Дата добавления: 2014-11-26