Постоянная сила, действующая на точку

Задача 2.4. (27.2)

Тяжелое тело спускается по гладкой плоскости, наклоненной под углом 30⁰ к горизонту. Найти, за какое время тело пройдет путь 9,6 м, если в начальный момент его скорость равнялась 2 м/с.

Решение

Рис. 2.5

На рис. 2.5. схематично представлено движение груза по наклонной плоскости. На тело действуют силы: 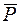– сила тяжести груза, 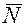– сила реакции опоры, так как поверхность гладкая по условию задачи, то силой трения пренебрежем. Выберем за начало движения исходное положение груза на наклонной плоскости (точка 0), ось х направим в сторону движения груза.

Составим дифференциальное уравнение движения груза по наклонной плоскости:

.

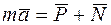Спроектируем это векторное уравнение на ось х:

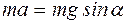. (1)

Здесь учтено, что проекция ускорения 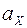равна по модулю a, так как ускорение груза направлено вдоль оси х.

Из уравнения (1) следует, что

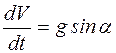. (2)

Уравнение (2) представляет дифференциальное уравнение с разделяющимися переменными:

.

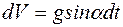Интегрируя это выражение, получим:

,

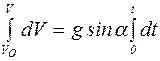где V₀ – скорость груза в начальный момент времени.

Отсюда следует, что

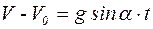, или

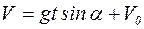, так как 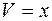, то

.

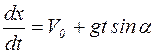Это дифференциальное уравнение первого порядка с разделяющимися переменными:

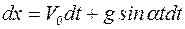
Интегрируя это выражение, получим:

.

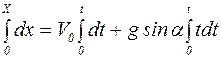Отсюда следует, что:

.

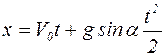Подставляя исходные данные: V₀ = 2 м/с, х = 9,6 м и преобразовывая, получим:

.

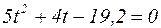Решая это квадратное уравнение, получим:

.

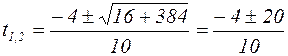Отсюда t₁ = -2,4 t₂ = 1,6, так как время может быть только положительным, поэтому выбираем t = 1,6 с.

Ответ: t = 1,6 с.

Дата добавления: 2014-11-26