Динамика относительного движения точки

Лекция 3

Законы динамики (законы Ньютона) верны для инерциальных систем отсчета (движение в которых называется абсолютным).

Рассмотрим движение материальной точки в неинерциальной системе отсчета.

Пусть материальная точка М движется под действием приложенных к ней сил 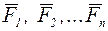. Рассмотрим движение этой системы по отношению к осям 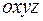, которые движутся относительно неподвижных осей 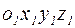(рис. 3.1).

Рис. 3.1

Определить зависимость между относительным ускорением точки и действующими на нее силами. Для абсолютного движения основной закон динамики имеет вид:

, (3.1)

где 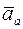– абсолютное ускорение точки.

Из кинематики сложного движения точки известно, что:

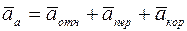, (3.2)

где 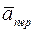– переносное ускорение точки,

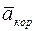– кориолисово ускорение точки.

Выведем обозначение: 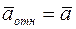, тогда

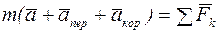, или

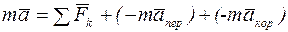. (3.3)

Пусть 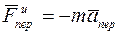– переносная сила инерции

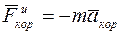– кориолисова сила инерции.

Тогда уравнение (3) примет вид:

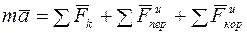. (3.4)

Уравнение (4) выражает основной закон динамики для относительного движения точки.

Из уравнений (1) и (4) следует, что уравнения и теоремы механики для относительного движения точки составляются так же, как и уравнения абсолютного движения, если при этом к действующим на точку силам взаимодействия с другими телами прибавить переносную и кориолисову силы инерции.

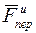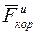Прибавление сил и учитывает влияние на относительное движение точки перемещения подвижных осей.

Рассмотрим некоторые частные случаи.

1. Если подвижные оси движутся поступательно, то 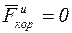, так как в этом случае ( – угловая скорость вращения подвижных осей координат); 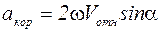, тогда . В этом случае уравнение (4) примет вид:

. (3.5)

2. Если подвижные оси перемещаются поступательно, равномерно и прямолинейно, то 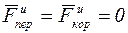и закон относительного движения будет иметь такой же вид, как и закон движения по отношению к неподвижным осям. Следовательно, такая система отсчета также будет инерциальной.

3. Если точка по отношению к подвижным осям находится в покое, то для нее и а, следовательно, и 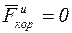, так как кориолисово ускорение 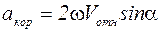. Тогда равенство (4) примет вид:

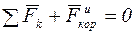. (3.6)

Уравнение (6) представляет собой уравнение относительного равновесия (покоя) точки. Из него следует, что уравнения относительного равновесия составляются так же, как уравнения равновесия в неподвижных осях, если при этом к действующим на точку силам взаимодействия с другими телами добавить переносную силу инерции.

4. При составлении уравнений относительного движения в случаях, когда 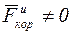, надо иметь в виду, что

, (3.7)

Поэтому сила 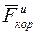перпендикулярна к 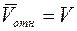, а значит и к касательной к относительной траектории точки. Следовательно:

а) проекция кориолисовой силы инерции на касательную к относительной траектории точки всегда равна нулю 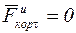и уравнение в относительном движении будет иметь вид:

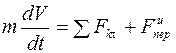, (3.8)

б) работа кориолисовой силы инерции на любом относительном перемещении равна нулю и теорема об изменении кинетической энергии в относительном движении будет иметь вид:

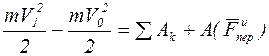, (3.9)

Задачи динамики относительно движения материальной точки рекомендуется решать в следующем порядке:

1. Разложить абсолютное движение материальной точки на относительное и переносное; выбрать неподвижную систему отсчета, связанную с подвижной средой, совершающей переносное движение;

2. записать начальные условия относительного движения материальной точки;

3. изобразить на рисунке силы , приложенные к материальной точке;

4. определить ускорение материальной точки в переносном движении 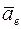, ускорение Кориолиса 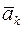, найти силы инерции в переносном движении , кориолисову силу инерции 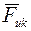. Добавить эти силы инерции к силам , приложенным к материальной точке;

5. составить дифференциальные уравнения:

;

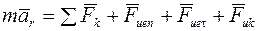– если переносное движение вращается вокруг неподвижной оси;

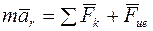– если переносное движение поступательное;

– если переносное движение равномерное и прямолинейное.

6. проинтегрировать составленные дифференциальные уравнения, определив постоянные интегрирования с помощью начальных условий движения;

7. определить искомые величины.

При решении прямой задачи, т.е. при определении сил по заданному движению пункты 2 и 6 надо опустить.

Задача 3.2 (33.2)

Точка привеса математического маятника длиной 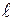движется по вертикали равноускоренно. Определить период Т малых колебаний маятника в двух случаях: 1) когда ускорение точки привеса направлено вверх и имеет какую угодно величину 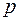; 2) когда это ускорение направлено вниз и величина его .

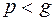Решение

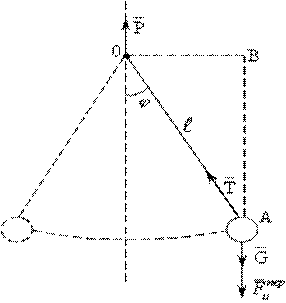
Рис. 3.2

На рис. 3.2 показан схематично математический маятник, точка подвеса которого «О» движется ускоренно вверх с ускорением 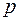. Рассмотрим положения маятника в некотором произвольном положении при отклонении нити маятника на угол .

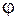Движение груза маятника вокруг точки подвеса «О» является относительным, а движение подвеса вверх – переносное.

На груз маятника действуют силы: 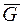– сила тяжести груза маятника, 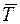– сила натяжения нити маятника, – сила инерции, действующая на груз маятника вследствие ускоренного движения точки подвеса. Так как ускорение точки подвеса направлено вверх, то сила инерции будет направлена в противоположную сторону относительно направления ускорения точки подвеса.

Применим дифференциальное уравнение для вращательного движения твердого тела для груза маятника:

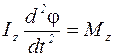, (1)

где 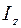– момент инерции маятника относительно оси, проходящий через точку подвеса и перпендикулярно плоскости чертежа:

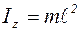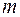, – масса груза маятника.

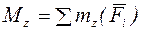– сумма моментов сил относительно оси .

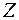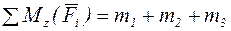, (2)

где – момент инерции силы тяжести относительно оси ;

– момент инерции силы натяжения нити относительно оси ;

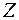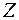– момент инерции силы инерции вследствие ускоренного движения точки подвеса относительно оси .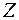

Значение момента будет равно:

. (3)

Момент силы натяжения нити относительно оси 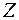равен нулю, так как направление силы проходит через ось: .

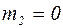Значение момента будет равно:

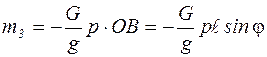. (4)

Подставляя выражения (3) и (4) в формулу (2), получим:

.

После преобразования этого выражения, получим:

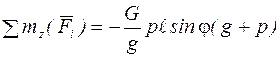. (5)

Подставляя выражение (5) в формулу (1), получим:

.

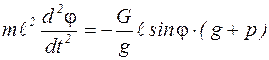Так как , то после преобразования, получим:

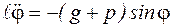, или

.

Учитывая, что колебания малые, то , тогда

.

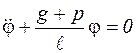Это дифференциальное уравнение описывает свободные колебания. Тогда частота собственных колебаний маятника будет:

.

Так как , где 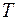– период колебания маятника, то

.

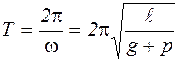Таким образом, если точка подвеса маятника перемещается вверх с ускорением 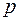, то период колебания маятника будет равен:

.

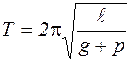Рассмотрим случай, когда точка подвеса перемещается вниз с ускорением 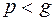(рис. 3.4).

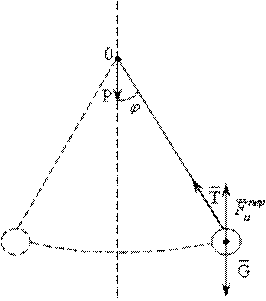
Рис. 3.4

В этом случае на груз маятника действуют силы 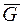и 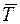так же как и в первом случае, а сила направлена в сторону, противоположную ускорению 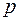(рис. 3.4). Тогда момент силы инерции относительно оси 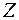будет:

.

Сумма моментов сил, действующих на груз маятника, будет

,

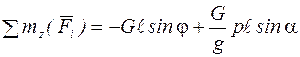после преобразований, получим:

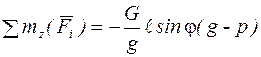. (6)

Подставляя выражение (6) в уравнение (1), получим:

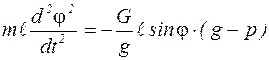
Учитывая, что , после подстановки и преобразований, получим:

.

Так как колебания малые, то , тогда

.

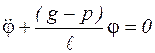Данное дифференциальное уравнение описывает свободные колебания с собственной частотой, равной

.

Тогда 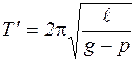– период колебания маятника при движении точки подвеса вниз с ускорением .

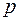Ответ: 1. ;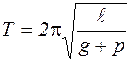

2. .

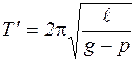Вопросы для самоконтроля:

1. Как определяется сила инерции тела?

2. Как определяется абсолютное ускорение при относительном движении точки?

Задачи, рекомендуемые для самостоятельного решения: 33.1. – 33.18. [3].

Литература: [1] – [5].

Дата добавления: 2014-11-26