Сила, действующая на точку, зависит от скорости

Сила, действующая на точку, зависит от координаты

Задача 2.1.

Найти уравнение движения тела массой m движущегося под действием силы F = ax, где а – постоянная величина. В начальный момент времени V = V₀, x₀ = 0.

Решение.

На рис. 2.2 представлено тело в произвольном положении М (х > 0; 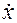>0). На тело действует сила F = ax.

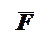
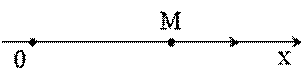
Рис. 2.2.

По второму закону Ньютона:

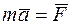
Спроектировав это уравнение на ось х, получим:

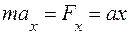
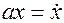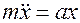Так как , то: , отсюда следует, что

.

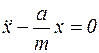Это дифференциальное однородное уравнение второго порядка. Для его решения составим характеристическое уравнение:

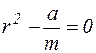
Отсюда следует, что 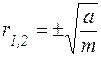, тогда решение дифференциального уравнения имеет вид:

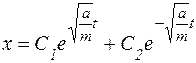
Согласно начальных условий имеем:

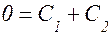
, так как 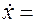V₀ при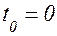

то 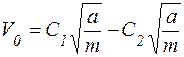, тогда С₁ = -С₂

_{; ;} ,

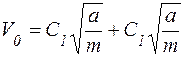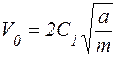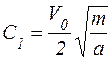тогда .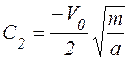

Уравнение движения тела имеет вид:

.

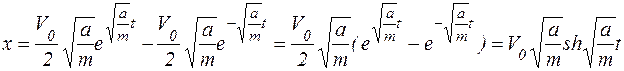
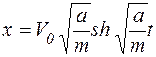Ответ: .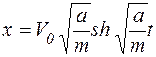

Задача 2.2. (27.18)

Подводная лодка, не имевшая хода, получив небольшую отрицательную плавучесть p, погружается на глубину, двигаясь поступательно. Сопротивление воды при небольшой отрицательной плавучести можно принять пропорциональным первой степени скорости погружения и равным KSV, где K – коэффициент пропорциональности, S – площадь горизонтальной проекции лодки, V – величина скорости погружения. Масса лодки m. Определить скорость погружения V, если при t = 0 скорость V₀ = 0.

Решение.

По условию задачи лодка имеет отрицательную плавучесть. Это означает, что сила тяжести лодки больше, чем сила Архимеда и разность этих сил равна Р.

Рассмотрим лодку как точечное тело. К лодке приложены: 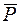– сила отрицательной плавучести, – сила сопротивления воды при погружении (рис. 2.3). Выберем начало координат в исходном положении лодки, а ось х направим по направлению погружения.

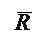
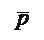
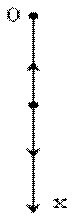
Рис. 2.3

Составим дифференциальное уравнение движения лодки:

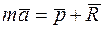
Спроектируем это векторное уравнение на ось х:

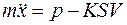, или:

.

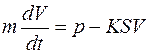Разделим обе части уравнения на массу:

.

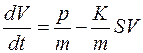Разделим переменные в этом дифференциальном уравнения первого порядка:

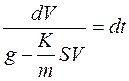, проинтегрируем это уравнение:

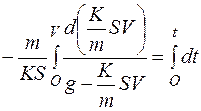, после интегрирования получим:

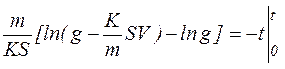
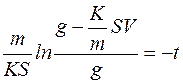, отсюда следует, что

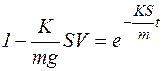, отсюда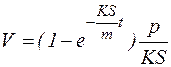

Ответ: .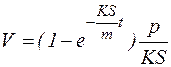

Дата добавления: 2014-11-26