Свободные колебания точки без учета сил сопротивления

Прямолинейные колебания материальной точки

Лекция 4

Под прямолинейными колебаниями точки понимают периодическое повторение движения вдоль одной прямой.

Гармоническими называются колебания, при которых отклонение точки от некоторого положения изменяется по закону синуса или косинуса.

Колебания, совершающиеся только под действием одной восстанавливающей силы, называются свободными.

Пусть точка М движется прямолинейно под действием восстанавливающей силы 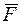, направленной всегда к неподвижному центру О и модуль этой силы пропорционален расстоянию до центра. Проекция силы 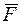на ось ох будет равна (рис. 4.1.):

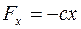
Рис. 4.1

Определим закон движения точки М массой m под действием силы 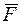. Запишем II закон Ньютона для точки М в произвольном направлении:

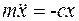, (4.1)

Разделив обе части уравнения на массу, получим:

.

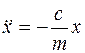Обозначим 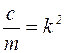, тогда

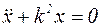. (4.2)

Уравнение (4.1) является дифференциальным уравнением свободных колебаний при отсутствии сил сопротивления. Для решения этого линейного однородного дифференциального уравнения второго порядка составим соответствующее характеристическое уравнение:

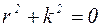, откуда следует, что .

Т.е. корни характеристического уравнения мнимые, поэтому решение уравнения (4.1) ищем в виде:

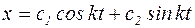, (4.3)

где С₁ и С₂ – постоянные коэффициенты, определяемые по начальным условиям.

Начальные условия задаются такие:

1. – положение точки в начальный момент времени, т.е. при .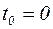

2. 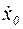– скорость точки в начальном положении при .

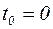Колебание, совершаемое телом по закону уравнения (4.1) называется гармоническим.

Обозначим 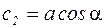; 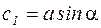и, подставив в уравнение (4.2), получим:

.

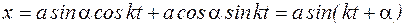Величина а, равная наибольшему отклонению точки от положения равновесия называется амплитудой колебания.

Величина 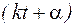называется фазой колебания, а угол α является начальной фазой колебаний.

Величина k называется круговой частотой колебаний и равна угловой скорости вращения точки вокруг центра.

, (4.4)

Промежуток времени Т, в течение которого точка совершает одно полное колебание, называется периодом колебаний:

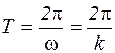, (4.5)

Величина , обратная периоду колебаний называется частотой. Частота определяет число колебаний совершаемых за одну секунду.

, (4.6)

Основные свойства свободных колебаний без сил сопротивления:

1. Амплитуда и начальная фаза колебаний зависят от начальных условий.

2. Частота и период колебаний не зависят от начальных условий и являются постоянными характеристиками данной системы (они зависят от массы и коэффициента жесткости).

Дата добавления: 2014-11-26