Влияние постоянной силы на свободные колебания точки

Пусть на точку М массой m кроме восстанавливающей силы 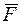, направленной к центру, действует постоянная по модулю и направлению сила 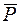. Вследствие воздействия силы 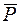новым центром равновесия точки М будет центр О₁, отстающий от О на расстояние 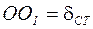(рис. 4.2), которое определяется равенством:

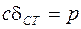
Рис. 4.2

Величина 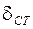называется статическим отклонением точки. Примем центр О₁ за начало отсчета и направим ось х в сторону действия силы 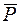. Составим дифференциальное уравнение движения точки. Для произвольного положения точки М будет (в проекциях на ось ох):

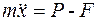, или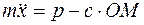

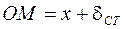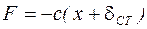Так как , то , тогда

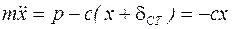, так как .

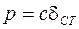Отсюда следует, что дифференциальное уравнение движения точки М имеет следующий вид:

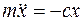, или разделим обе части уравнения на массу, получим:

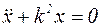, где 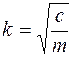. (4.7)

Полученное уравнение совпадает с уравнением (4.2). Таким образом, постоянная сила не изменяет характера колебаний, совершаемых точкой под действием восстанавливающей силы F, а только смещает центр этих колебаний в сторону действия силы на величину статического отклонения.

Определим период колебаний.

Из уравнения (4.3) следует, что:

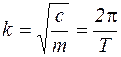, т.е. ,

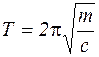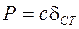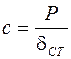так как , то , отсюда: .

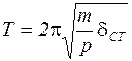Задача 4.1 (32.4.)

Груз Q, падая с высоты 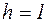м без начальной скорости, ударяется об упругую горизонтальную балку в ее середине; концы балки закреплены. Написать уравнение дальнейшего движения груза на балке, отнеся движение к оси, проведенной вертикально вниз из положения статического равновесия груза на балке, если статический прогиб балки в ее середине при указанной нагрузке равен 0,5 см; массой балки пренебречь.

Решение

Рис. 4.3

Направим ось х по вертикали вниз, взяв за начало отсчета О положение статического равновесия груза (рис. 4.3). В положении статического равновесия балка прогибается на величину статического равновесия 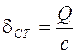, где С – коэффициент упругости балки.

Рассмотрим груз в положении, смещенном относительно нуля на х вниз и предположим, что груз движется вниз в сторону возрастания х. Балка прогибается и ее сила упругости ,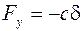

где: δ – смещение середины балки из ненагруженного состояния, т.е. 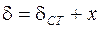, тогда

.

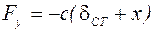Кроме силы 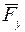к грузу приложена сила тяжести .

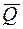Составим уравнение движения груза под действием данных сил:

.

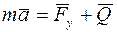Проектируя это векторное уравнение на ось х, получим:

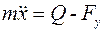, или

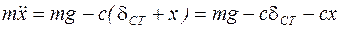. (1)

Учитывая, что в состоянии равновесия: 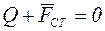или в проекции на ось х, получим 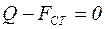, где 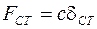, тогда

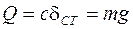. (2)

Учитывая это, выражение (1) примет вид:

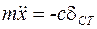, или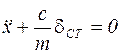

Обозначим 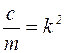, тогда . (3)

Для решения этого дифференциального уравнения второго порядка составим соответствующее характеристическое уравнение:

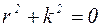, отсюда

.

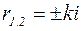Так как корни мнимые и различные, то решением уравнения (3) будет:

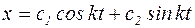. (4)

Определим численное значение :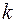

.

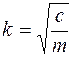Так как из уравнения (2) следует, что , тогда

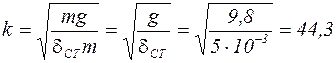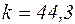(с^-1).

с^-1

Тогда уравнение (4) примет вид:

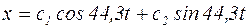. (5)

Постоянные С₁ и С₂ определим из начальных условий: при 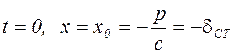, а так как груз падает с высоты h, то начальную скорость можно определить следующим образом.

При падении груза с высоты h, конечная скорость будет:

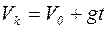, так как груз падает без начальной скорости, т.е. 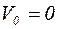, то

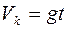, отсюда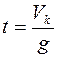

Так как 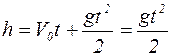, , 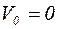тогда

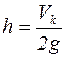, отсюда .

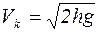Подставляя численные значения, получим: 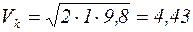(м/с)

м/с.

Конечная скорость груза при падении является начальной скоростью движения середины балки (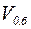), тогда

м/с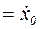

Подставляя в уравнение (5) полученные условия, получим:

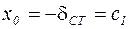; или .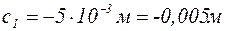

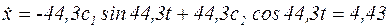
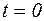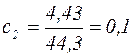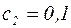при , получим: , или (м).

м.

Тогда уравнение движения (5) примет вид:

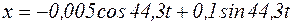(м)

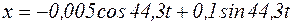Ответ: (м).

Дата добавления: 2014-11-26