Криволинейное движение точки

Рассмотрим свободную материальную точку, движущуюся под действием сил , , 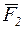… . Выберем неподвижную систему координат o x y z (рис. 2.6.)

Рис. 2.6.

Составим уравнение движения точки:

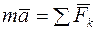. (2.8)

Спроектируем векторное уравнение на оси координат:

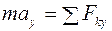; ; , (2.9)

Учитывая, что ; ; 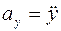, получим дифференциальные уравнения криволинейного движения точки.

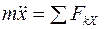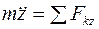; ; . (2.10)

Уравнения (2.10) позволяют решать как первую, так и вторую задачи динамики.

Начальные условия задаются в виде: при t = 0

x = x₀, y = y₀, z = z₀

V_x = V_xo, V_y = V_yo, V_z = V_oz

Задача 2.5 (27.52)

Тело весом Р, брошенное с начальной скоростью V₀ под углом α к горизонту, движется под влиянием силы тяжести и сопротивления R воздуха. Определить наибольшую высоту h тела над уровнем начального положения, считая сопротивление пропорциональным первой степени скорости: .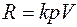

Решение.

Рис. 2.7

Выберем систему координат с центром в точке начала движения тела (рис. 2.7). Рассмотрим силы, действующие на тело в произвольном положении в точке М траектории: – сила тяжести тела; и – силы сопротивления по осям у и х. Тогда уравнения движения тела будут:

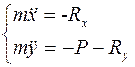(1), (2)

Так как нас интересует наибольшая высота подъема тела, то рассмотрим вертикальную составляющую движения тела:

, или

Разделяя переменные в этом дифференциальном уравнении первого порядка, получим:

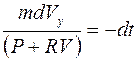. (3)

Так как: 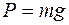; , тогда подставляя эти выражения в дифференциальное уравнение (3), получим:

. (4)

Интегрируя уравнение (4), получим:

;

;

.

После преобразований получим:

.

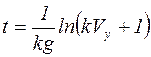Так как , то

. (5)

Определим уравнение движения тела в вертикальном направлении. Воспользуемся уравнением (2):

Отсюда следует, что 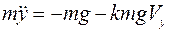, т.е.

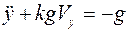, или

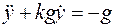. (6)

Это дифференциальное уравнение второго порядка, неоднородное. Решение уравнения (6) представим в виде:

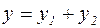
где у₁ – общее решение однородного дифференциального уравнения;

у₂ – частное решение однородного дифференциального уравнения.

– однородное дифференциальное уравнение, составим соответствующее характеристическое уравнение: , отсюда 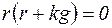. Поэтому ; . Тогда решение у₁ имеет вид:

.

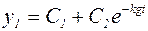Решение у₂ ищем в виде:

,

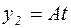так как одним корнем характеристического уравнения есть ноль, тогда:

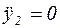, , отсюда при подстановке этих выражений в уравнение (6), получим:

, или .

Тогда 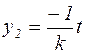, поэтому

.

По начальным условиям: t₀ = 0; x₀ = 0; V_oy = V_oy, следует:

С₁ + С₂ = 0, т.е. С₁ = – С_{2 ,}

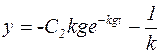, или подставляя начальные условия, получим:

, отсюда .

Тогда , поэтому

,

после преобразований, получим:

. (7)

(7) является уравнением движения тела в вертикальном направлении.

Верхней точки траектории тело достигает за время, определяемое выражением (5), тогда с учетом, что , получим, что наибольшая высота поднятия тела:

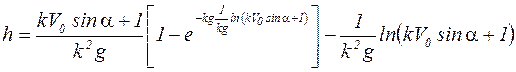. (8)

Так как по определению логарифма числа: 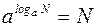, то выражение (8) преобразуется:

.

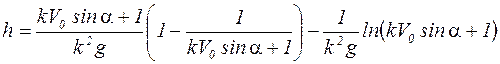Отсюда следует, что:

.

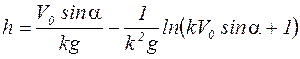Ответ: наибольшая высота поднятия тела равна:

.

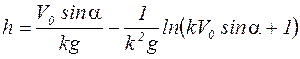Задача 2.6 (27.53)

В условиях предыдущей задачи 2.5 (27.52) найти уравнения движения тела.

Решение

В решении предыдущей задачи показано, что уравнение вертикального движения тела имеет вид (7):

учитывая, что 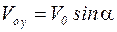, тогда

. (1)

В горизонтальном движении дифференциальное уравнение движения имеет вид (см. предыдущую задачу, выражение (1)):

, тогда

, отсюда следует, что

. (2)

Для решения однородного дифференциального уравнения второго порядка составим характеристическое уравнение:

, отсюда

, поэтому r₁ = 0; r₂ = - kg.

Тогда решение уравнения (2) имеет вид:

.

Постоянные С₁ и С₂ определим по начальным условиям: t₀ = 0; x₀ = 0;

V_ox = V_ocosα.

или , отсюда: ,

тогда 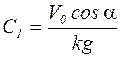, отсюда

,

. (3)

Выражение (3) представляет уравнение движения тела в горизонтальной плоскости.

Ответ: ,

.

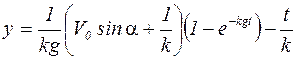Задача 2.7 (27.54)

При условии задачи (27.52) определить, на каком расстоянии S по горизонтали точка достигнет наивысшего положения.

Решение.

Из решения задачи 2.6 (27.53) уравнение движения тела в горизонтальной плоскости имеет вид:

. (1)

Время движения тела до наивысшей точки траектории составляет (см. решение задачи (27.52)):

. (2)

Подставляя выражение (2) в уравнение (1), получим:

.

.

Ответ: Расстояние по горизонтали, когда тело достигнет наивысшей точки: .

Вопросы для самоконтроля:

1. Методика решения задач при прямолинейном движении точки?

2. Методика решения задач при криволинейном движении точки?

Задачи, рекомендуемые для самостоятельного решения: 27.1 – 27.68. [3].

Литература: [1] – [5].

Дата добавления: 2014-11-26