Прямолинейное движение материальной точки

Дифференциальные уравнения движения

Лекция № 2

материальной точки и их интегрирование

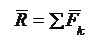Рассмотрим прямолинейное движение точки под действием приложенных к ней силы . Положение точки на траектории определяется ее координатой Х (рис. 1).

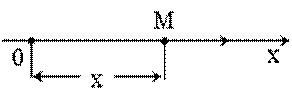
Рис. 2.1.

Основная задача динамики в этом случае состоит в том, чтобы, зная R, найти закон движения точки, т.е. x = f(t).

Согласно второго закона Ньютона:

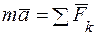, (2.1)

проектируя это векторное уравнение на ось х,получим:

.

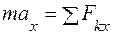Учитывая, что ускорение точки при прямолинейном движении направлено вдоль линии движения, то .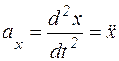

Тогда 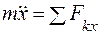, (2.2)

Так как , то (2.3)

В тех случаях, когда при решении задачи необходимо искать зависимость скорости от координаты х,а не от времени t,тогда надо перейти к другой переменной:

, тогда (2.3) примет вид:

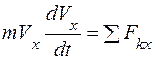; или , (2.4)

Решение основной задачи динамики сводится к тому, чтобы из данных уравнений, зная силы, найти закон движения точки, т.е. x = f(t). Для этого надо проинтегрировать соответствующее дифференциальное уравнение. В общем случае силы могут зависеть от координаты (х), скорости (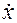) и времени (t).

Тогда уравнение (2) примет вид:

. (2.5)

Уравнение (5) представляет собой дифференциальное уравнение 2 ^го порядка. Общее решение такого уравнения будет иметь вид:

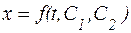, (2.6)

где С₁, С₂ – постоянные коэффициенты, определяемые по начальным условиям.

За начальный момент обычно принимают момент начала движения. Положение, которое точка занимает в начальный момент, называется начальным положением, а ее скорость в этот момент – начальной скоростью. Например, начальные условия могут быть заданы следующим образом: t = 0; x = x_0; V_x = V₀.

По начальным условиям можно определить конкретные значения постоянных С₁ и С₂ и найти частное решение уравнения (2.5), дающее закон движения точки, в виде:

. (2.7)

Рекомендации для решения задач.

Решение задач динамики путем интегрирования соответствующих дифференциальных уравнений движения сводиться к следующим операциям:

1. Составление дифференциального уравнения движения.

Для составления дифференциального уравнения движения надо:

а) Выбрать начало отсчета (обычно совмещая с начальным положением точки) и провести координатную ось вдоль линии движения, направляя ее, как правило, в сторону движения, если под действием приложенных сил точка может находиться в положении равновесия, то начало отсчета удобно помещать в положение статического равновесия.

б) Изобразить движущуюся точку в произвольном положении (но так, чтобы было х > 0 и V_x > 0) и показать все действующие на точку силы.

в) Подсчитать сумму проекций всех сил на координатную ось и подставить эту сумму в правую часть дифференциального уравнения движения. При этом надо обязательно все переменные силы выразить через те величины (t, x или V), от которых эти силы зависят.

2. Интегрирование дифференциального уравнения движения.

Интегрирование производится методами известными в математике.

3. Определение постоянных интегрирования.

Для определения постоянных интегрирования необходимо знать начальные условия. Значения начальных условий подставляются в общее решение дифференциального уравнения результатом которого является получение двух линейных уравнений с двумя неизвестными (С₁ и С₂). Решая эту систему уравнений определим постоянные интегрирования (С₁ и С₂).

Рассмотрим решение некоторых задач, в которых сила зависит от координаты, скорости и времени.

Дата добавления: 2014-11-26