
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свободные колебания при сопротивлении, пропорциональном скорости (затухающие колебания)
|
|
|
|
Пусть на материальную точку М массой m действуют восстанавливающая сила 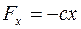 и сила сопротивления
и сила сопротивления 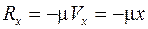 (Рис.4.4). Дифференциальное уравнение движения будет:
(Рис.4.4). Дифференциальное уравнение движения будет:
 .
.

Рис. 4.4
Разделив обе части уравнения на массу, получим:
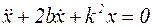 , (4.8)
, (4.8)
где 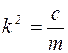 ;
;  .
.
Уравнение (1) представляет собой дифференциальное однородное уравнение второго порядка. Для его решения составим соответствующее характеристическое уравнение:
 . (4.9)
. (4.9)
4. Рассмотрим случай, когда k>b, т.е. сопротивление мало по сравнению с восстанавливающей силой.
Пусть 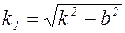 , тогда, как следует из выражения (2), корни характеристического уравнения будут комплексными. В этом случае решение уравнения (1) ищем в виде:
, тогда, как следует из выражения (2), корни характеристического уравнения будут комплексными. В этом случае решение уравнения (1) ищем в виде:
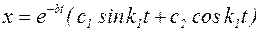 , (4.10)
, (4.10)
где с1 и с2 – постоянные коэффициенты, определяемые по начальным условиям. Делая замену: 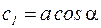 и
и 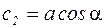 и тригонометрические преобразования, получим:
и тригонометрические преобразования, получим:
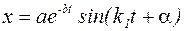 . (4.11)
. (4.11)
Колебания, происходящие по закону (4.8) называются затухающими (рис.4.5).

Рис. 4.5
Период затухающих колебаний определяется по формуле:
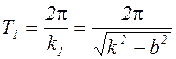 , (4.12)
, (4.12)
Величина, равная отношению двух амплитуд, различающихся на величину периода колебания, называется декрементом колебаний:
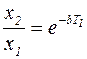 , (4.13)
, (4.13)
Прологарифмировав это выражение, получим:
 , (4.14)
, (4.14)
Величина, равная 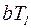 , называется логарифмическим декрементом затухания.
, называется логарифмическим декрементом затухания.
5. Рассмотрим случай, когда b>k, т.е. сила сопротивления велика по сравнению с восстанавливающей.
Обозначим 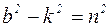 , тогда корни квадратного уравнения (4.12) будут действительные и отрицательные. В этом случае решение уравнения (1) ищем в виде:
, тогда корни квадратного уравнения (4.12) будут действительные и отрицательные. В этом случае решение уравнения (1) ищем в виде:
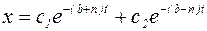 , (4.15)
, (4.15)
График такого движения показан на рис. 4.6
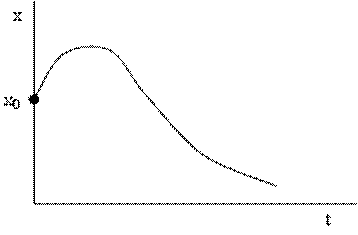
Рис. 4.6
Движение, совершаемое материальной точкой по закону, описываемое уравнением (4) является периодическим, так как описывается периодической функцией, т.е. это колебательный процесс. Так как амплитуда колебания с течением времени асимптотически приближается к статическому положению равновесия, то это затухающие колебания. Действительно найдем предел, к которому стремится функция в уравнении (4) при увеличении времени:
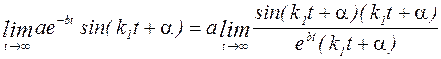 , (4.16)
, (4.16)
Учитывая, что 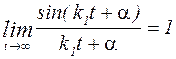 (первый замечательный предел),
(первый замечательный предел),
то 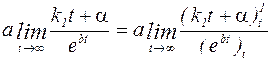 (примем правило Лопиталя), получим, что
(примем правило Лопиталя), получим, что  . Это означает, что амплитуда колебания асимптотически стремится к нулю.
. Это означает, что амплитуда колебания асимптотически стремится к нулю.
3. Рассмотрим случай, когда k<b, т.е. сила сопротивления больше восстанавливающей силы. В этом случае в уравнении (2) дискриминант будет положительным, т.е.
 , пусть
, пусть 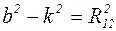 .
.
В этом случае корни характеристического уравнения (4.12) будут действительные и отрицательные: 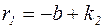 ;
;  . Тогда решение уравнения (1) будет иметь вид:
. Тогда решение уравнения (1) будет иметь вид:
 (4.17)
(4.17)
Проанализируем это выражение. Движение, описываемое уравнением (5) не является периодическим, так как входящие в нее экспоненциальные функции – не периодические. Это движение затухающее, так как отклонение точки от положения статического равновесия с течением времени приближается к нему, т.е. 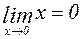 . Действительно:
. Действительно:
 .
.
Иными словами это движение является затухающим. На рис. 4.7 представлены графики – это движения в зависимости от начальных условий.
а) 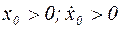 , т.е. направление скорости совпадает с возрастанием отклонения.
, т.е. направление скорости совпадает с возрастанием отклонения.
б)  , т.е. направление скорости противоположно направлению оси х и не очень большая.
, т.е. направление скорости противоположно направлению оси х и не очень большая.
в)  , т.е. направление скорости противоположно направлению оси х и больше по величине.
, т.е. направление скорости противоположно направлению оси х и больше по величине.
Во всех случаях а, б, в движения будут затухающими и непериодическими.
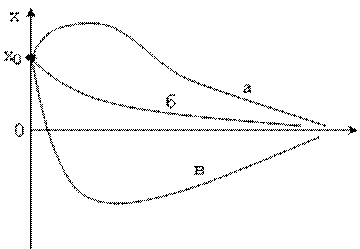
Рис. 4.7
6. Рассмотрим случай, когда  , тогда корни характеристического уравнения (2) будут равны и отрицательны. Поэтому решение уравнения (1) ищем в виде:
, тогда корни характеристического уравнения (2) будут равны и отрицательны. Поэтому решение уравнения (1) ищем в виде:
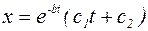 . (4.18)
. (4.18)
Движение, описываемое уравнением (6), является непериодическим, так как включает линейную и экспоненциальные функции и затухающим, т.е.  .
.
Задача 4.2 (32.93)
Тело весом 2 кГ, прикрепленное пружиной к неподвижной точке А, движется по гладкой наклонной плоскости, образующей угол 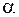 с горизонтом, под действием возмущающей силы
с горизонтом, под действием возмущающей силы 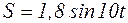 кГ и силы сопротивления, пропорциональной скорости:
кГ и силы сопротивления, пропорциональной скорости: 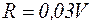 кГ. (рис. 4.8). Коэффициент жесткости пружины
кГ. (рис. 4.8). Коэффициент жесткости пружины 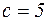 кГ/см. В начальный момент тело находилось в покое в положении статического равновесия. Найти уравнение движения тела, периоды
кГ/см. В начальный момент тело находилось в покое в положении статического равновесия. Найти уравнение движения тела, периоды 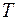 свободных и
свободных и 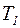 вынужденных колебаний, сдвиг фазы вынужденных колебаний и возмущающей силы.
вынужденных колебаний, сдвиг фазы вынужденных колебаний и возмущающей силы.
Решение

Рис. 4.8
Обозначим силы, действующие на груз: 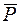 – сила тяжести груза,
– сила тяжести груза, 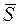 – возмущающая сила,
– возмущающая сила, 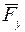 – сила упругости пружины,
– сила упругости пружины,  – сила сопротивления. Поместим начало координат в точку статического равновесия и направим ось х по направлению растяжения пружины. Составим дифференциальное уравнение движения груза:
– сила сопротивления. Поместим начало координат в точку статического равновесия и направим ось х по направлению растяжения пружины. Составим дифференциальное уравнение движения груза:
 .
.
Спроектируем это векторное уравнение на ось х:
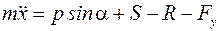 , (1)
, (1)
где  ;
;
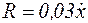 ;
;
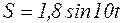 ;
;
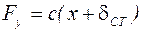 .
.
Подставляя эти выражения в уравнение (1), получим:
 .
.
Учитывая, что 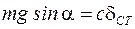 – при статическом равновесии.
– при статическом равновесии.
После преобразований, получим:
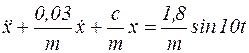 , или
, или
 .
.
Подставляя численные значения, получим:
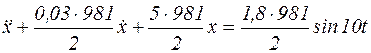 ,
,
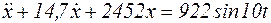 . (2)
. (2)
Решение полученного дифференциального неоднородного уравнения второго порядка ищем в виде:
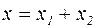 ,
,
где 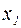 – общее решение однородного дифференциального уравнения;
– общее решение однородного дифференциального уравнения;
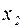 – частное решение неоднородного дифференциального уравнения.
– частное решение неоднородного дифференциального уравнения.
Однородное дифференциальное уравнение имеет вид:
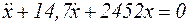 .
.
Для решения этого однородного дифференциального уравнения составим характеристическое уравнение:
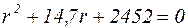 .
.
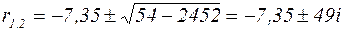 , так как корни характеристического уравнения комплексные, то решение ищем в виде:
, так как корни характеристического уравнения комплексные, то решение ищем в виде:
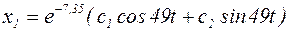 .
.
Решение 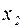 ищем в виде:
ищем в виде:
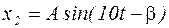 ,
,
где 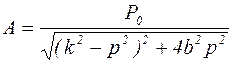 ;
; 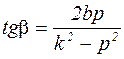 .
.
Коэффициент 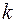 определяется из формулы:
определяется из формулы:
 ; тогда:
; тогда:  ,
,
подставляя численные значения, получим:
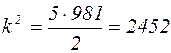 ;
;  ;
; 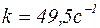 .
.
Так как  , по условию задачи
, по условию задачи 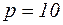 ,
, 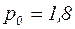 , тогда
, тогда
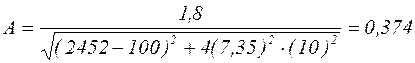 .
.
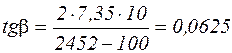 ;
;  ;
;  .
.
Отсюда следует, что 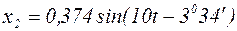 .
.
Решение уравнения (1) будет иметь вид:
 . (3)
. (3)
Коэффициенты С1 и С2 определим из начальных условий: 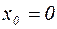 ,
, 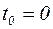 ,
, 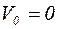 . Подставим начальные условия в уравнение (3):
. Подставим начальные условия в уравнение (3):
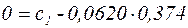 ;
; 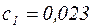 .
.
Продифференцируем уравнение (3) по времени и подставим начальные условия:
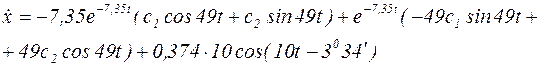 .
.
Подставив начальные условия, получим:
 .
.
Тогда решение уравнения (2) будет иметь вид:
 .
.
Ответ:  .
.
Вопросы для самоконтроля:
1. Что такое свободные колебания?
2. Что такое затухающие колебания?
3. Что такое апериодическое движение?
Задачи, рекомендуемые для самостоятельного решения: 32.1 – 32.50., 32.51. – 32.74. [3].
Литература: [1] – [5].
|
|
|
|
|
Дата добавления: 2014-11-26; Просмотров: 1104; Нарушение авторских прав?; Мы поможем в написании вашей работы!