
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вынужденные колебания при наличии сопротивления
|
|
|
|
Рассмотрим движение точки М массой m, на которую действуют: восстанавливающая сила 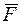 , сила сопротивления
, сила сопротивления  , пропорциональная первой степени скорости, а возмущающая сила
, пропорциональная первой степени скорости, а возмущающая сила  (рис. 5.5). Дифференциальное уравнение движения точки М будет:
(рис. 5.5). Дифференциальное уравнение движения точки М будет:
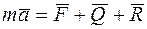

Рис. 5.5
Спроектируем это векторное уравнение на ось ох, получим:
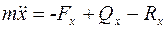 , (5.17)
, (5.17)
Так как  ;
; 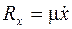 ,
,  , то
, то
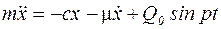 , (5.18)
, (5.18)
разделив обе части уравнения на массу, получим:
 , (5.19)
, (5.19)
Введя обозначения: 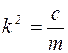 ;
;  ;
; 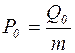 , получим
, получим
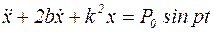 , (5.20)
, (5.20)
Это дифференциальное уравнение неоднородное второго порядка, решение его ищем в виде:
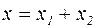 , (5.21)
, (5.21)
где 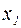 – общее решение однородного дифференциального уравнения.
– общее решение однородного дифференциального уравнения.
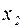 – частное решение неоднородного дифференциального уравнения.
– частное решение неоднородного дифференциального уравнения.
Соответствующее однородное уравнение имеет вид:
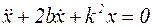 , (5.22)
, (5.22)
Для его решения составим характеристическое уравнение:
 , (5.23)
, (5.23)
Найдем корни этого квадратного уравнения:
 .
.
При 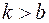 решение представлено равенством (4).
решение представлено равенством (4).
 , (5.24)
, (5.24)
где 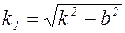 , постоянные
, постоянные 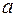 и
и 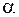 определяются по начальным условиям.
определяются по начальным условиям.
Частное решение 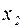 ищем в виде:
ищем в виде:
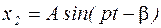 , (5.25)
, (5.25)
где 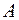 и
и  – постоянные, при которых уравнение (1) становится тождеством. Вычисляя производные
– постоянные, при которых уравнение (1) становится тождеством. Вычисляя производные  ,
, 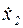 и подставляя их в уравнение (5.23) получим:
и подставляя их в уравнение (5.23) получим:
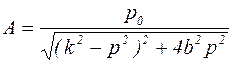 ;
; 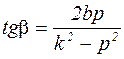 .
.
Отсюда следует, что постоянные 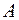 и
и  не зависят от начальных условий. Угол
не зависят от начальных условий. Угол  характеризует сдвиг фаз между вынужденными колебаниями и возмущающей силой.
характеризует сдвиг фаз между вынужденными колебаниями и возмущающей силой.
Решение уравнения (5.23) можно представить в виде:
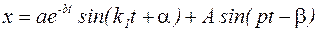 . (5.26)
. (5.26)
Видно, что решение (4) состоит из собственных колебаний (первое слагаемое) и вынужденных (второе слагаемое).
Собственные колебания являются затухающими.
На рис. 5.6 представлены: 5.6 а – собственные затухающие колебания; 5.6б – вынужденные колебания; 5.6 в – результирующее колебание.
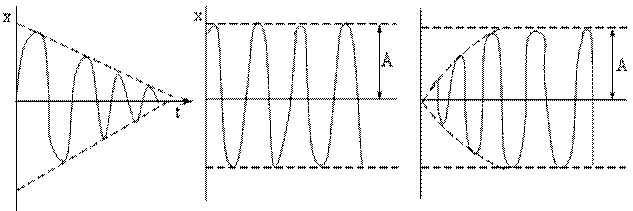
а) б) в)
Рис. 5.6
Задача 5.2 (32.88)
На пружине, коэффициент жесткости которой 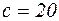 г/см, подвешены магнитный стержень весом 50 г, проходящий через соленоид и медная пластинка весом 50 г, проходящая между полюсами магнита. По соленоиду течет ток
г/см, подвешены магнитный стержень весом 50 г, проходящий через соленоид и медная пластинка весом 50 г, проходящая между полюсами магнита. По соленоиду течет ток 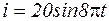 ампер и развивает силу взаимодействия с магнитным стержнем
ампер и развивает силу взаимодействия с магнитным стержнем 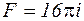 дин. Сила торможения медной пластинки, вследствие вихревых токов равна
дин. Сила торможения медной пластинки, вследствие вихревых токов равна 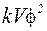 , где
, где 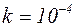 ,
, 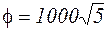 единиц CGS и
единиц CGS и  – скорость пластины. Определить вынужденные колебания пластинки.
– скорость пластины. Определить вынужденные колебания пластинки.
Решение

а) б)
Рис. 5.7
На рис. 5.7 а) схематично представлено условие задачи. Стержень силой тяжести  и пластину силой тяжести
и пластину силой тяжести  представим как материальную точку силой тяжести
представим как материальную точку силой тяжести  . На рис. 5.7 б) она представлена материальной точкой С массой
. На рис. 5.7 б) она представлена материальной точкой С массой 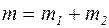 , где
, где  и
и  – массы соответственно стержня и пластины.
– массы соответственно стержня и пластины.
На материальную точку С действуют: 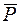 – сила тяжести,
– сила тяжести, 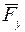 – сила упругости пружины,
– сила упругости пружины, 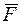 – сила взаимодействия магнитного стержня и соленоида,
– сила взаимодействия магнитного стержня и соленоида,  – сила торможения вследствие вихревых токов.
– сила торможения вследствие вихревых токов.
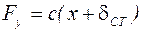 , где
, где 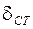 – статическое отклонение, равное
– статическое отклонение, равное 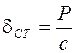 ;
; 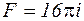 , так как
, так как 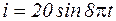 , то:
, то:  .
.
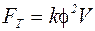 , где
, где 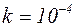 ,
, 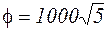 , учитывая, что
, учитывая, что 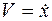 , то:
, то: 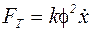 .
.
Составим уравнение второго закона Ньютона для материальной точки С, находящаяся под действием сил 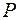 ,
, 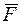 ,
,  ,
, 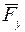 :
:
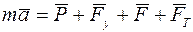 . (1)
. (1)
Спроектируем векторное уравнение (1) на ось х:
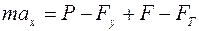 .
.
Учитывая, что 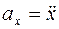 и подставляя выражения сил, получим:
и подставляя выражения сил, получим:
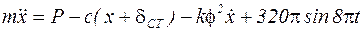 . (2)
. (2)
После преобразования дифференциального уравнения (2), получим:
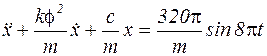 . (3)
. (3)
Обозначим  ,
, 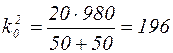 ,
, 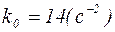 ;
;
 ,
, 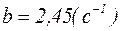 ;
;
 ,
, 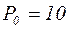 (м/с2).
(м/с2).
По условию задачи частота возмущающей силы равна  . Подставив полученные обозначения в уравнение (3), получим:
. Подставив полученные обозначения в уравнение (3), получим:
 . (4)
. (4)
Уравнение вынужденных колебаний будем искать в виде:
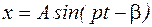 , (5)
, (5)
где 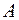 – амплитуда вынужденных колебаний, равная
– амплитуда вынужденных колебаний, равная
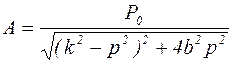 , (6)
, (6)
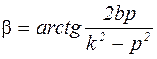 . (7)
. (7)
Подставив численные значения в выражения (6) и (7), получим:
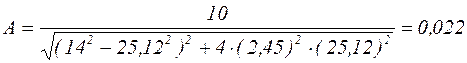 (см)
(см)
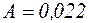 см.
см.
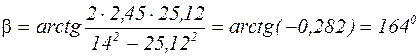
или  .
.
Подставив полученные значения в уравнение (4), получим:
 , см.
, см.
Ответ: вынужденные колебания пластины –
 см.
см.
Вопросы для самоконтроля:
1. Что такое вынужденные колебания?
2. Что такое явление резонанса?
Задачи, рекомендуемые для самостоятельного решения: 32.75. – 32.101. [3].
Литература: [1] – [5].
|
|
|
|
|
Дата добавления: 2014-11-26; Просмотров: 1444; Нарушение авторских прав?; Мы поможем в написании вашей работы!