
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Системы векторов. Базисы
|
|
|
|
ЛИНЕЙНО ЗАВИСИМЫЕ И ЛИНЕЙНО НЕЗАВИСИМЫЕ
Пусть
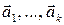 – (1)
– (1)
конечная система векторов,
 – (2)
– (2)
произвольные вещественные числа. Вектор

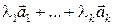 (3)
(3)
называется линейной комбинацией системы векторов (1) с коэффициентами (2). Говорят также, что  линейно выражается через систему векторов (1).
линейно выражается через систему векторов (1).
Линейная комбинация (3) называется тривиальной, если все коэффициенты равны нулю: 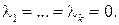 Ясно, что тривиальная линейная комбинация любой системы векторов равна нулевому вектору:
Ясно, что тривиальная линейная комбинация любой системы векторов равна нулевому вектору: 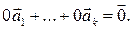 Линейная комбинация (3) называется нетривиальной, если среди коэффициентов (2) есть ненулевые числа.
Линейная комбинация (3) называется нетривиальной, если среди коэффициентов (2) есть ненулевые числа.
В математике принято различать системы векторов двух типов: линейно независимые и линейно зависимые. Системы первого типа – это такие системы векторов, для которых нулевой вектор нельзя получить никакой другой линейной комбинацией, кроме тривиальной. Такова, например, система, состоящая из одного ненулевого вектора:  Действительно, равенство
Действительно, равенство 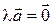 возможно только, если
возможно только, если 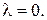 С другой стороны, легко привести примеры таких систем векторов, для которых существуют нетривиальные линейные комбинации, равные нулевому вектору. Например, такова система
С другой стороны, легко привести примеры таких систем векторов, для которых существуют нетривиальные линейные комбинации, равные нулевому вектору. Например, такова система  состоящая из двух равных векторов, так как
состоящая из двух равных векторов, так как 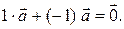 Перейдем к точным определениям.
Перейдем к точным определениям.
Определение 1.4.1. Система векторов (1) называется линейно зависимой, если существует нетривиальная линейная комбинация системы (1), равная нулевому вектору. Система векторов, не являющаяся линейно зависимой, называется линейно независимой.
Более подробно, определение 1.4.1 означает следующее. Система векторов (1) линейно зависима, если существует набор чисел  среди которых есть ненулевые, такой, что
среди которых есть ненулевые, такой, что 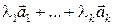
 Система векторов (4) линейно независима, если только тривиальная линейная комбинация этих векторов равна нулевому вектору, т. е. из равенства
Система векторов (4) линейно независима, если только тривиальная линейная комбинация этих векторов равна нулевому вектору, т. е. из равенства 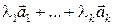
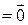 следует, что
следует, что 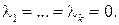
Далее рассмотрим алгебраические и геометрические критерии линейной зависимости и независимости векторов.
Утверждение 1.4.1. Система, состоящая из одного вектора, линейно зависима тогда и только тогда, когда этот вектор нулевой.
Доказательство. Если  – нулевой вектор, то
– нулевой вектор, то 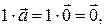 т.е. существует нетривиальная линейная комбинация вектора
т.е. существует нетривиальная линейная комбинация вектора  , равная нулевому вектору. Обратно, пусть для некоторого вектора
, равная нулевому вектору. Обратно, пусть для некоторого вектора  существует число
существует число 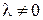 такое, что
такое, что  Переходя в последнем равенстве к длинам, получаем:
Переходя в последнем равенстве к длинам, получаем: 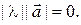 Так как
Так как 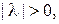 то
то 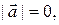 т.е.
т.е. 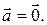
Утверждение 1.4.2. Система, содержащая более одного вектора, линейно зависима тогда и только тогда, когда один из векторов системы линейно выражается через другие.
Доказательство. Необходимость. Пусть
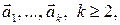 – (4)
– (4)
линейно зависимая система векторов. Существует набор чисел  среди которых есть ненулевые, такой, что
среди которых есть ненулевые, такой, что
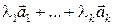
 (5)
(5)
Пусть, для определенности, 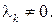 Умножим обе части равенства (5) на
Умножим обе части равенства (5) на 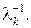 Получим:
Получим:
 или
или
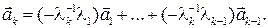
Итак, вектор 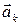 линейно выражается через другие векторы системы.
линейно выражается через другие векторы системы.
Достаточность. Пусть один из векторов системы (4) линейно выражается через остальные, например,  Тогда
Тогда
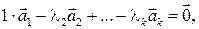
т.е. существует нетривиальная линейная комбинация векторов системы, равная нулевому вектору. Значит, система (4) линейно зависима.
Упражнение 1.4.1. Докажите, система векторов является линейно зависимой, если выполняется одно из условий:
(i) система содержит нулевой вектор;
(ii) система содержит повторяющиеся векторы;
(iii) система содержит линейно зависимую подсистему.
Определение 1.4.2. Базисом множества 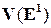 векторов прямой
векторов прямой 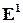 называется ненулевой вектор
называется ненулевой вектор 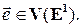
Теорема 1.4.1. Пусть 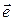 – базис множества
– базис множества 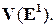 Тогда любой вектор
Тогда любой вектор  линейно выражается через
линейно выражается через 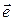 :
:
 (6)
(6)
Число  определяется однозначно и называется координатой вектора
определяется однозначно и называется координатой вектора  в данном базисе.
в данном базисе.
Доказательство. Если  то
то  т.е.
т.е.  Пусть
Пусть  Отложим векторы
Отложим векторы  и
и 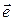 от некоторой точки
от некоторой точки 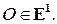 Получим соответственно точки А и Е на прямой
Получим соответственно точки А и Е на прямой 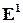 , отличные от точки О (рис. 4.1).
, отличные от точки О (рис. 4.1).
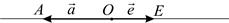
Рис. 4.1
Тогда, очевидно,  если точки А и Е лежат на одном луче с вершиной в точке О, либо
если точки А и Е лежат на одном луче с вершиной в точке О, либо  если точки А и Е лежат на различных лучах с вершиной в точке О. Таким образом,
если точки А и Е лежат на различных лучах с вершиной в точке О. Таким образом, 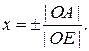 Для любого вектора доказана возможность представления в виде (6). Докажем единственность такого представления. Пусть наряду с (6) верно равенство:
Для любого вектора доказана возможность представления в виде (6). Докажем единственность такого представления. Пусть наряду с (6) верно равенство:
 (7)
(7)
Из (7) и (6) вытекает, что 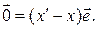 Поскольку вектор
Поскольку вектор 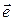 ненулевой, то
ненулевой, то 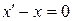 , т.е.
, т.е. 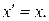
Итак, если на прямой зафиксирован базис, то любой вектор этой прямой имеет однозначно определяемую координату  в этом базисе. Если
в этом базисе. Если  – координата вектора
– координата вектора  в данном базисе, то используют запись
в данном базисе, то используют запись 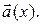 Отметим, что в случае, когда длина базисного вектора
Отметим, что в случае, когда длина базисного вектора 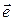 равна 1, то координата
равна 1, то координата  вектора
вектора  с точностью до знака совпадает с его длиной:
с точностью до знака совпадает с его длиной: 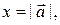 если
если 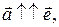 либо
либо  если
если 
Утверждение 1.4.3. Система, состоящая из двух векторов, линейно зависима тогда и только тогда, когда векторы системы коллинеарны.
Доказательство. Необходимость. Пусть  – линейно зависимая система векторов. По утверждению 1.4.2, один из векторов линейно выражается через другой, т.е.
– линейно зависимая система векторов. По утверждению 1.4.2, один из векторов линейно выражается через другой, т.е. 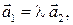 или
или 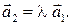 Следовательно, векторы
Следовательно, векторы  и
и 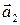 коллинеарны.
коллинеарны.
Достаточность. Пусть  – коллинеарные векторы. Если они оба нулевые, то, очевидно, система
– коллинеарные векторы. Если они оба нулевые, то, очевидно, система  линейно зависима. Пусть один из векторов, например,
линейно зависима. Пусть один из векторов, например,  ненулевой. Отложим векторы
ненулевой. Отложим векторы  от некоторой точки О, получим соответственно точки
от некоторой точки О, получим соответственно точки  и
и 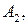 лежащие на прямой
лежащие на прямой 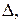 проходящей через точку О. Таким образом, можно считать, что
проходящей через точку О. Таким образом, можно считать, что  – векторы прямой
– векторы прямой 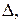 причем
причем  можно взять в качестве базиса множества
можно взять в качестве базиса множества 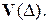 По теореме 1.4.1,
По теореме 1.4.1,  т.е. один из векторов системы линейно выражается через другой. Согласно утверждению 1.3.2, система
т.е. один из векторов системы линейно выражается через другой. Согласно утверждению 1.3.2, система  линейно зависима.
линейно зависима.
Следствие 1.4.1. Два вектора линейно независимы тогда и только тогда, когда они неколлинеарны.
Определение 1.4.3. Базисом множества 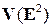 векторов плоскости
векторов плоскости  называется упорядоченная пара
называется упорядоченная пара 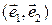 неколлинеарных векторов этой плоскости.
неколлинеарных векторов этой плоскости.
Теорема 1.4.2. Пусть 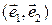 – базис множества
– базис множества 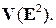 Тогда любой вектор
Тогда любой вектор 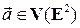 линейно выражается через базис (раскладывается по базису):
линейно выражается через базис (раскладывается по базису):
 (6)
(6)
Числа  и
и 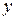 определяются однозначно и называются координатами вектора
определяются однозначно и называются координатами вектора  в данном базисе.
в данном базисе.
Доказательство. Если вектор  нулевой, то
нулевой, то  т.е. для этого вектора
т.е. для этого вектора 
Пусть  Отложим векторы
Отложим векторы 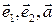 от некоторой точки
от некоторой точки  Получим соответственно точки
Получим соответственно точки  отличные от точки О. Обозначим
отличные от точки О. Обозначим  прямую, проходящую через точки
прямую, проходящую через точки  и
и 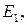
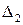 – прямую, проходящую через точки
– прямую, проходящую через точки  и
и  (рис.4.2).
(рис.4.2).
Если вектор  коллинеарен вектору
коллинеарен вектору 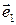 , то точка А лежит на прямой
, то точка А лежит на прямой 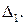 В этом случае можно считать, что
В этом случае можно считать, что  и
и 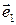 – векторы прямой
– векторы прямой  причем
причем 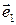 – базис множества
– базис множества 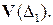 Тогда, согласно теореме 1.4.1,
Тогда, согласно теореме 1.4.1,  Аналогично доказывается возможность представления (6) в случае, когда вектор
Аналогично доказывается возможность представления (6) в случае, когда вектор  коллинеарен второму базисному вектору.
коллинеарен второму базисному вектору.
Пусть вектор  не коллинеарен ни одному из базисных векторов. Проведем через точку А прямые
не коллинеарен ни одному из базисных векторов. Проведем через точку А прямые  и
и  , параллельные соответственно
, параллельные соответственно  и
и 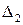 . Пусть
. Пусть  – точка пересечения прямых
– точка пересечения прямых  и
и 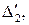
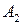 – точка пересечения
– точка пересечения 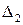 и
и  . По построению,
. По построению,  – параллелограмм (рис.4.2).
– параллелограмм (рис.4.2).
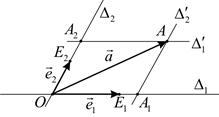
Рис. 4.2
Векторы 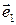 и
и 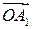 – векторы прямой
– векторы прямой  причем
причем 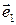 – базис множества
– базис множества 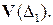 Согласно теореме 1.4.1, существует число
Согласно теореме 1.4.1, существует число  такое, что
такое, что  Аналогично, существует число
Аналогично, существует число 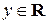 такое, что
такое, что 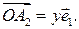 По правилу параллелограмма
По правилу параллелограмма 
Итак, для любого вектора 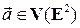 доказана возможность разложения (6). Однозначность чисел
доказана возможность разложения (6). Однозначность чисел  и
и 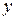 в (6) следует из линейной независимости векторов
в (6) следует из линейной независимости векторов 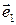 и
и 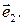 Действительно, пусть наряду с (6) верно равенство
Действительно, пусть наряду с (6) верно равенство
 (7)
(7)
Вычисляя разность (7) и (6), получаем  Так как
Так как 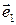 и
и 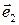 линейно независимы, то
линейно независимы, то  т.е.
т.е. 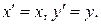
Если 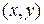 – координаты вектора
– координаты вектора  в данном базисе, то используют запись
в данном базисе, то используют запись 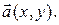 Будем использовать также следующие матричные обозначения:
Будем использовать также следующие матричные обозначения:
 – матрица-строка базисных векторов;
– матрица-строка базисных векторов;
 – вектор -столбец координат.
– вектор -столбец координат.
В таких обозначениях вектор есть произведение матриц:
 [1]
[1]
Итак, короткая матричная запись равенства (6) имеет вид:
 (
( )
)
Утверждение 1.4.4. Система, состоящая из трех векторов, линейно зависима тогда и только тогда, когда векторы системы компланарны.
Доказательство. Необходимость. Пусть  – линейно зависимая система векторов. По утверждению 1.4.2, один из векторов линейно выражается через другие. Пусть, для определенности,
– линейно зависимая система векторов. По утверждению 1.4.2, один из векторов линейно выражается через другие. Пусть, для определенности,  Существует плоскость
Существует плоскость 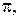 которой параллельны векторы
которой параллельны векторы  и
и  Поскольку
Поскольку 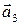 линейно выражается через
линейно выражается через  и
и 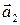 , то вектор
, то вектор 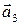 также параллелен плоскости
также параллелен плоскости 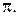 Следовательно, векторы
Следовательно, векторы  компланарны.
компланарны.
Достаточность. Пусть  – компланарные векторы. Можно считать, что
– компланарные векторы. Можно считать, что  – векторы некоторой плоскости
– векторы некоторой плоскости 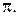 Если векторы
Если векторы  и
и 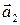 не коллинеарны, то их можно взять в качестве базиса множества
не коллинеарны, то их можно взять в качестве базиса множества 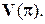 По теореме 1.4.2, существуют числа
По теореме 1.4.2, существуют числа  такие, что
такие, что 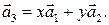 Так как один из векторов линейно выражается через другие, то, по утверждению 1.4.2, система
Так как один из векторов линейно выражается через другие, то, по утверждению 1.4.2, система  линейно зависима. Если же векторы
линейно зависима. Если же векторы  и
и 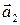 коллинеарны, то, согласно утверждению 1.4.3, система
коллинеарны, то, согласно утверждению 1.4.3, система  линейно зависима. А тогда система
линейно зависима. А тогда система  также линейно зависима.
также линейно зависима.
Следствие 1.4.2. Три вектора линейно независимы тогда и только тогда, когда они некомпланарны.
Определение 1.4.4. Базисом множества 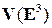 векторов пространства
векторов пространства 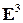 называется упорядоченная тройка
называется упорядоченная тройка  некомпланарных векторов.
некомпланарных векторов.
Теорема 1.4.3. Пусть  – базис множества векторов пространства
– базис множества векторов пространства  Тогда любой вектор
Тогда любой вектор 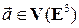 линейно выражается через базис (раскладывается по базису):
линейно выражается через базис (раскладывается по базису):
 (8)
(8)
Числа  определяются однозначно и называются координатами вектора
определяются однозначно и называются координатами вектора  в данном базисе.
в данном базисе.
Доказательство. Доказательство этой теоремы аналогично доказательству теоремы 1.4.2. Вначале доказывается возможность представления любого вектора в виде (8), а затем его единственность.
Отложим векторы  от одной точки О. Возникают три точки
от одной точки О. Возникают три точки 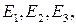 не лежащие с точкой О в одной плоскости, три прямые
не лежащие с точкой О в одной плоскости, три прямые 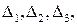 определяемые соответственно парами точек
определяемые соответственно парами точек 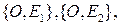
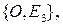 и три плоскости
и три плоскости  определяемые соответственно тройками точек
определяемые соответственно тройками точек 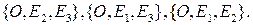 Вектор
Вектор  также откладывается от точки О, возникает точка А такая, что
также откладывается от точки О, возникает точка А такая, что 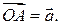 (рис. 4.3).
(рис. 4.3).

Рис. 4.3
Если точка 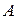 принадлежит плоскости
принадлежит плоскости  то векторы
то векторы 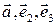 можно считать векторами этой плоскости и поскольку векторы
можно считать векторами этой плоскости и поскольку векторы  линейно независимы, то они составляют базис множества
линейно независимы, то они составляют базис множества 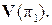 По теореме 1.4.2 вектор
По теореме 1.4.2 вектор  можно разложить по этому базису:
можно разложить по этому базису:  Разложение (8) в таком случае имеет вид:
Разложение (8) в таком случае имеет вид: 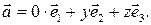 Аналогично доказывается возможность разложения (8) в случаях, когда
Аналогично доказывается возможность разложения (8) в случаях, когда 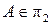 или
или 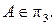
Пусть точка 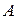 не принадлежит ни одной из плоскостей
не принадлежит ни одной из плоскостей  Спроектируем точку А на каждую прямую
Спроектируем точку А на каждую прямую  параллельно плоскости
параллельно плоскости 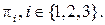 Возникают точки
Возникают точки 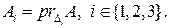 Согласно правилу параллелепипеда, верно следующее равенство:
Согласно правилу параллелепипеда, верно следующее равенство:
 (9)
(9)
Далее раскладываем каждый вектор  по базисному вектору
по базисному вектору  соответствующей прямой:
соответствующей прямой:  Подставляя эти разложения в равенство (9), получаем искомое равенство (8).
Подставляя эти разложения в равенство (9), получаем искомое равенство (8).
Однозначность чисел  в (8) следует из линейной независимости векторов
в (8) следует из линейной независимости векторов  и доказывается также, как в теореме 1.4.2.
и доказывается также, как в теореме 1.4.2.
Если  – координаты вектора
– координаты вектора  в данном базисе, то применяют запись
в данном базисе, то применяют запись  Будем использовать также матричные обозначения, аналогичные случаю плоскости:
Будем использовать также матричные обозначения, аналогичные случаю плоскости:
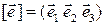 – матрица-строка базисных векторов;
– матрица-строка базисных векторов;
 – вектор -столбец координат.
– вектор -столбец координат.
В таких обозначениях короткая матричная запись равенства (8) имеет вид:
 (
(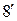 )
)
Утверждение 1.4.4. Любаясистема векторов пространства  содержащая более трех векторов, линейно зависима.
содержащая более трех векторов, линейно зависима.
Доказательство. Пусть  – система векторов, состоящая из четырех или более векторов. Если векторы
– система векторов, состоящая из четырех или более векторов. Если векторы  некомпланарны, то они образуют базис множества
некомпланарны, то они образуют базис множества 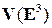 и, следовательно, четвертый вектор линейно выражается через первые три. По утверждению 1.4.2, система
и, следовательно, четвертый вектор линейно выражается через первые три. По утверждению 1.4.2, система 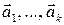 линейно зависима. Если же векторы
линейно зависима. Если же векторы  компланарны, то они линейно зависимы, следовательно, линейно зависима и данная система векторов
компланарны, то они линейно зависимы, следовательно, линейно зависима и данная система векторов 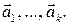
Утверждение 1.4.5. Координаты вектора, являющегося линейной комбинацией системы векторов, есть такие же линейные комбинации соответствующих координат векторов системы.
Доказательство. Проведемдоказательство для случая пространства, в случаях прямой и плоскости рассуждения не меняются, уменьшается только число координат. Пусть  – базис множества векторов пространства
– базис множества векторов пространства 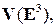
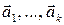 – система векторов,
– система векторов, 
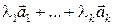 – их линейная комбинация. Пусть
– их линейная комбинация. Пусть  – координаты вектора
– координаты вектора 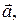
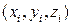 – координаты векторов
– координаты векторов  в данном базисе.
в данном базисе.
Разложим векторы  и
и  по базисным векторам:
по базисным векторам:


и подставим эти выражения в равенство 
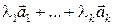 . Пользуясь свойствами операций над векторами, получим:
. Пользуясь свойствами операций над векторами, получим:
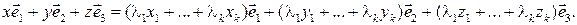
Так как координаты вектора в данном базисе определяются однозначно, то верны равенства

выражающие заключение доказываемого утверждения.
Следствие 1.4.1. Пусть 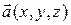 и
и 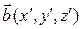 – векторы, заданные своими координатами в некотором базисе,
– векторы, заданные своими координатами в некотором базисе,  – вещественное число. Тогда векторы
– вещественное число. Тогда векторы  и
и 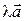 имеют в этом базисе следующие координаты:
имеют в этом базисе следующие координаты:

Среди множества всех базисов выделяют так называемые ортонормированные базисы, которые, как будет видно в дальнейшем, удобны при вычислениях.
Определение 1.4.5. Ортонормированным базисом называется базис, векторы которого попарно ортогональны и имеют единичную длину.
Обычно ортонормированные базисы на плоскости обозначаются  в пространстве –
в пространстве –  (рис. 4.4).
(рис. 4.4).

Рис. 4.4
С помощью базисов можно ввести понятие ориентации прямой, плоскости и пространства.
Пусть 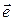 и
и  – базисы прямой
– базисы прямой 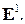 Направления двух ненулевых векторов прямой могут быть совпадающими, либо противоположными. В первом случае будем говорить, что базисы
Направления двух ненулевых векторов прямой могут быть совпадающими, либо противоположными. В первом случае будем говорить, что базисы 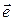 и
и  одинаково ориентированы, во-втором – противоположно ориентированы. Очевидно, что отношение одинаковой ориентируемости является отношением эквивалентности [2]в множестве всех базисов. Следовательно, множество всех базисов разбивается на классы эквивалентности – классы одинаково ориентированных базисов. Понятно, что таких классов ровно два, столько же, сколько направлений на прямой. Выбор одного из двух классов одинаково ориентированных базисов называется ориентацией прямой. Таким образом, на прямой есть две ориентации; ориентировать прямую означает выбрать на ней одно из двух направлений.
одинаково ориентированы, во-втором – противоположно ориентированы. Очевидно, что отношение одинаковой ориентируемости является отношением эквивалентности [2]в множестве всех базисов. Следовательно, множество всех базисов разбивается на классы эквивалентности – классы одинаково ориентированных базисов. Понятно, что таких классов ровно два, столько же, сколько направлений на прямой. Выбор одного из двух классов одинаково ориентированных базисов называется ориентацией прямой. Таким образом, на прямой есть две ориентации; ориентировать прямую означает выбрать на ней одно из двух направлений.
Пусть 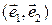 – базис на плоскости
– базис на плоскости  . Отложим векторы
. Отложим векторы 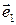 и
и 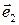 от некоторой точки О, получим соответственно точки
от некоторой точки О, получим соответственно точки 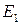 и
и  , не лежащие на одной прямой с точкой О (рис. 4.5).
, не лежащие на одной прямой с точкой О (рис. 4.5).

Рис. 4.5
Отрезок 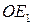 можно повернуть вокруг точки О на угол, не превосходящий полный угол так, чтобы он наложился на отрезок
можно повернуть вокруг точки О на угол, не превосходящий полный угол так, чтобы он наложился на отрезок 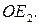 Cуществует два различных направления такого поворота. Поворачиваясь в одном направлении, отрезок
Cуществует два различных направления такого поворота. Поворачиваясь в одном направлении, отрезок 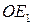 «заметет» угол, величина которого
«заметет» угол, величина которого  меньше
меньше 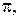 поворачиваясь в другом направлении, отрезок
поворачиваясь в другом направлении, отрезок 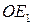 «заметет» угол, величина которого
«заметет» угол, величина которого 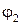 больше
больше  Разумеется, направления поворотов и величины соответствующих углов не зависят от выбора точки О. Допуская вольность речи, будем говорить, что поворачивая отрезки вокруг точки, мы поворачиваем соответствующие векторы вокруг этой точки.
Разумеется, направления поворотов и величины соответствующих углов не зависят от выбора точки О. Допуская вольность речи, будем говорить, что поворачивая отрезки вокруг точки, мы поворачиваем соответствующие векторы вокруг этой точки.
Пусть  и
и  – базисы на плоскости
– базисы на плоскости  Будем говорить, что эти базисы одинаково ориентированы, еслинаправления кратчайших поворотов первых базисных векторов до вторых в обоих базисах совпадают. В противном случае говорят, что базисы противоположно ориентированы. На рисунке 4.6, а) изображены одинаково ориентированные базисы, на рисунке 4.6, б) – противоположно ориентированные базисы.
Будем говорить, что эти базисы одинаково ориентированы, еслинаправления кратчайших поворотов первых базисных векторов до вторых в обоих базисах совпадают. В противном случае говорят, что базисы противоположно ориентированы. На рисунке 4.6, а) изображены одинаково ориентированные базисы, на рисунке 4.6, б) – противоположно ориентированные базисы.
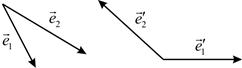

а) б)
Рис. 4.6
Как и в случае прямой, отношение одинаковой ориентируемости базисов на плоскости, очевидно, является отношением эквивалентности в множестве всех базисов плоскости. Следовательно, множество всех базисов разбивается на классы эквивалентности – классы одинаково ориентированных базисов. Ясно, что таких классов ровно два, столько же, сколько направлений поворотов вокруг точек. Выбор одного из двух классов одинаково ориентированных базисов называется ориентацией плоскости. Таким образом, на плоскости есть две ориентации; ориентировать плоскость означает выбрать на ней одно из двух возможных направлений поворотов вокруг точек (рис. 4.7, а), б)).

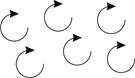
а) б)
Рис. 4.7
В пространстве 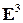 также как в случаях прямой и плоскости множество всех базисов разбивается на два класса, определяющих две ориентации пространства. Однако, в отличие от случаев прямой и плоскости, где невозможно отличить одну ориентацию от другой, в пространстве ориентации различаются, и одна из них называется правой, а другая – левой. Соответственно, базисы, составляющие первый класс, называются правыми,а базисы, составляющие второй класс, – левыми.
также как в случаях прямой и плоскости множество всех базисов разбивается на два класса, определяющих две ориентации пространства. Однако, в отличие от случаев прямой и плоскости, где невозможно отличить одну ориентацию от другой, в пространстве ориентации различаются, и одна из них называется правой, а другая – левой. Соответственно, базисы, составляющие первый класс, называются правыми,а базисы, составляющие второй класс, – левыми.
Пусть  – базис в пространстве
– базис в пространстве 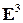 . Отложим векторы
. Отложим векторы  от некоторой точки О, получим соответственно точки
от некоторой точки О, получим соответственно точки  Обозначим
Обозначим 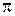 плоскость, проходящую через точки
плоскость, проходящую через точки  (рис. 4.8).
(рис. 4.8).


а) б)
Рис. 4.8
Поскольку векторы, составляющие базис, не компланарны, то точка 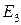 не лежит в плоскости
не лежит в плоскости 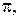 а лежит в одном из двух полупространств, на которые пространство разбивается плоскостью
а лежит в одном из двух полупространств, на которые пространство разбивается плоскостью 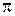 . Базис
. Базис  называется правым, если, глядя на плоскость
называется правым, если, глядя на плоскость 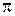 из точки
из точки 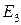 (из «конца» вектора
(из «конца» вектора  ), мы видим кратчайший поворот вектора
), мы видим кратчайший поворот вектора 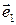 до вектора
до вектора 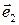 происходящим в направлении, противоположном направлению поворота часовой стрелки (рис. 4.8, а). Базис
происходящим в направлении, противоположном направлению поворота часовой стрелки (рис. 4.8, а). Базис  называется левым, если, глядя из «конца» вектора
называется левым, если, глядя из «конца» вектора  , мы видим кратчайший поворот вектора
, мы видим кратчайший поворот вектора 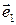 до вектора
до вектора 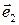 происходящим в направлении движения часовой стрелки (рис. 4.8, б). Моделями правого и левого базисов могут служить первые три пальца руки человека, соответственно правой и левой, расположенных в естественном положении (рис.).
происходящим в направлении движения часовой стрелки (рис. 4.8, б). Моделями правого и левого базисов могут служить первые три пальца руки человека, соответственно правой и левой, расположенных в естественном положении (рис.).
Этим объясняется употребление терминов правый и левый. Пользуясь этими моделями, легко убедиться, что справедливы следующие свойства ориентации:
(i) перестановка любых двух векторов в упорядоченной тройке некомпланарных векторов меняет ориентацию на противоположную;
(ii) замена одного из векторов в упорядоченной тройке некомпланарных векторов на противоположный вектор меняет ориентацию на противоположную.
Пусть  – три некомпланарных вектора. На их основе можно образовать 6 различных упорядоченных троек, из которых три тройки правых и три – левых. Действительно, зафиксируем одну их них – упорядоченную тройку
– три некомпланарных вектора. На их основе можно образовать 6 различных упорядоченных троек, из которых три тройки правых и три – левых. Действительно, зафиксируем одну их них – упорядоченную тройку  Каждая из троек
Каждая из троек 
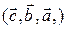 получена из данной перестановкой двух элементов, следовательно, каждая из троек
получена из данной перестановкой двух элементов, следовательно, каждая из троек  имеет ориентацию, противоположную ориентации тройки
имеет ориентацию, противоположную ориентации тройки  С другой стороны, тройки
С другой стороны, тройки  и
и  можно получить из тройки
можно получить из тройки 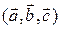 два раза переставляя пары элементов, следовательно, тройки
два раза переставляя пары элементов, следовательно, тройки 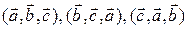 имеют одинаковую ориентацию.
имеют одинаковую ориентацию.
[1] Здесь в записи произведения вектора на число мы не различаем обозначения и
[2] См. [ ], §
|
|
|
|
|
Дата добавления: 2014-11-09; Просмотров: 2635; Нарушение авторских прав?; Мы поможем в написании вашей работы!