Основные свойства определителя III-го порядка

Ниже перечисленные свойства справедливы для определителя любого порядка, поэтому далее в формулировках мы не будем указывать порядок определителя.

1) определитель не меняет своего значения при замене всех его строк соответствующими столбцами;

2) при перестановке двух параллельных рядов определителя модуль определителя сохраняет прежнее значение, а знак меняется на противоположный;

3) определитель, у которого два параллельных ряда одинаковы, равен нулю;

4) общий множитель какого-либо ряда определителя можно выносить за знак определителя;

5) если все элементы какого-либо ряда равны нулю, то определитель равен нулю.

Решение систем линейных уравнений при помощи определителей.

Пусть дана система линейных алгебраических уравнений вида .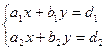

Данную систему можно решить, используя понятие определителя. Числа 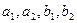– коэффициенты системы, 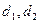– свободные члены.

Такую систему, в которой свободные члены находятся в правых частях, будем называть стандартной.

Под решением системы понимается всякая пара чисел 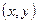, обращающая эту систему в тождество (верное равенство).

Для нахождения решений системы применим метод исключения неизвестных. Умножим первое уравнение системы на 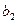, а второе – на 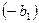. Получим:

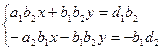
Сложим уравнения системы:

.

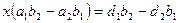
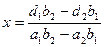Аналогично найдем 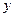. Для этого умножим первое уравнение системы на 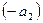, а второе уравнение – на 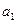и сложим. Получим:

.

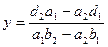Обратим внимание на знаменатели двух этих дробей. Они представляют собой разложение определителя второго порядка. Введем обозначения 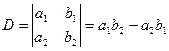. Введем также понятие дополнительных определителей системы: ; .

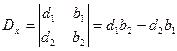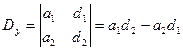Определител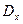и и 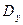получаются из определителя системы 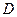путем замены коэффициентов при указанном неизвестном на соответствующие свободные члены.

Используя введенные обозначения, формулы для решения системы примут вид:

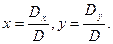
Данные формулы называются формулами Крамера.

Существуют три случая:

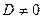
1) существует единственное решение, которое может быть найдено с помощью формул Крамера.

2) 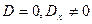и (или)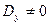 система несовместна (не имеет решений).

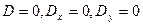
3) система имеет бесконечное множество решений.

Пример: Решить систему методом Крамера:

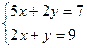
Дата добавления: 2014-11-09