Нормальный процесс

СТАЦИОНАРНОСТЬ И ЭРГОДИЧНОСТЬ СП.

Процесс считается строго стационарным (установившимся) или стационарным в узком смысле, если его n -мерные функции распределения не изменяются во времени, т.е. при сдвиге всех сечений на любой интервал времени t.

В практике, особенно в электротехническом приложении, чаще используется понятие стационарности в широком смысле или просто стационарности, если при сдвиге СП на интервал t не изменяются его двумерные характеристики. Таким образом, процесс можно считать стационарным, если неизменными во времени остаются его числовые характеристики – математическое ожидание , дисперсия D, а корреляционная функция 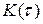зависит только от t, и не зависит от t.

Случайные процессы, стационарные в узком смысле, стационарны и в широком смысле, но не наоборот.

Введем понятие эргодичности СП. СП считается эргодическим, если для него одинаковых результатов при определении числовых характеристик можно добиться путем усреднения по времени и путем усреднения по множеству, например, .

Понятие эргодичности включает в себя понятие стационарности, но не наоборот, т.е. процесс может быть стационарным, но не эргодическим; будучи эргодическим, он обязательно стационарен.

При эргодичности процесса его числовые характеристики могут быть получены по одной достаточно длинной реализации, а результаты могут быть отнесены и к другим реализациям.

Вернемся к рассмотрению законов распределения СП.

Плотность вероятностей мгновенных значений СП тем больше, чем большее время он существует при данном значении.

Существует большое число изученных видов распределений, отличающихся друг от друга формой кривой f (x).

Одним из наиболее хорошо изученных видов распределений является нормальное или гауссовское. Вид кривой плотности вероятности мгновенных значений нормального СП определяется выражением: .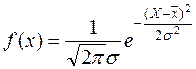

В зависимости от величины s кривые будут отличаться друг от друга (рис. 18, а).

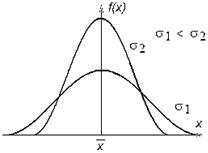
Рис 18

Все нормальные СП с разными s можно привести к одному графику.

Для этого СП нормируют: приводят к s =1, т. е. вводят новую переменную 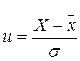. Тогда 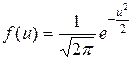, и график имеет вид, показанный на рис. 19.

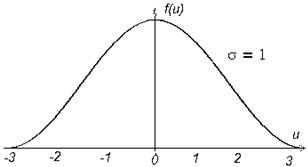
Рис. 19

Считается, что практически все (с вероятностью 0,9973) значения процесса попадают в интервал ±3 s. Отсюда, полный размах нормального СП равен приблизительно 6 s.

Реальные СП весьма часто близки к нормальным. Известно, что распределение суммы достаточно большого числа СП (больше 5) с произвольным законом распределения, среди которых нет преобладающих, является нормальным. Это – следствие т. н. центральной предельной теоремы.

Например, помехи в каналах связи часто имеют нормальное распределение.

Интегрирование графика, приведенного на рис. 19, позволяет поручить формулы для определения интегралов вероятностей:

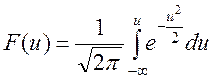, (1.7)

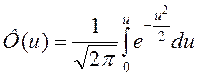. (1.8)

Использование интегралов вероятностей, известных как функция Лапласа (1.7) и Крампа (1.8), позволяет решать многие статистические задачи, в частности, связанные с надежностью и помехозащищенностью. Значения интегралов приводятся в таблицах.

График функции Крампа показан на рис. 20.

Ф (u)

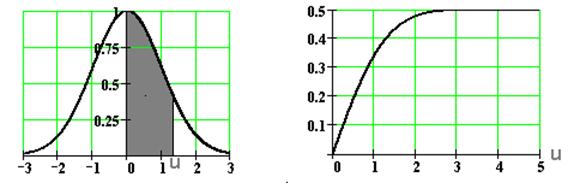
Рис. 20

Функция помогает определить вероятность ошибки при приеме двоичного символа (0 или 1) и воздействии нормированной гауссовой помехи, если пороговый уровень принятия решения имеет значение u. Вероятность ошибки численно будет равна Р _ош=0,5- Ф (u) (площадь незачерненного «хвостика»).

Лекция 5. (2 часа)

Дата добавления: 2014-11-16