Элементы векторной алгебры и аналитической геометрии в пространстве

Пример

Даны вершины треугольника 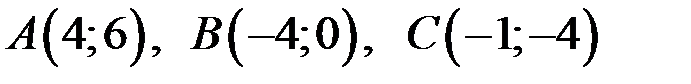. Найти:

1) уравнение стороны АВ;

2) уравнение медианы, проведенной из вершины С;

3) координату точки пересечения медиан;

4) уравнение высоты, опущенной из вершины В на сторону АС и ее длину;

5) уравнение прямой, проходящей через точку С параллельно прямой АВ;

6) площадь треугольника.

Решение

1) Используем уравнение прямой, проходящей через две точки 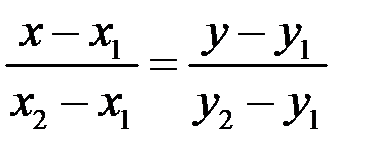. Подставив координаты точек 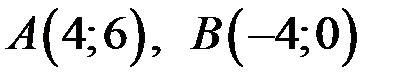, получим

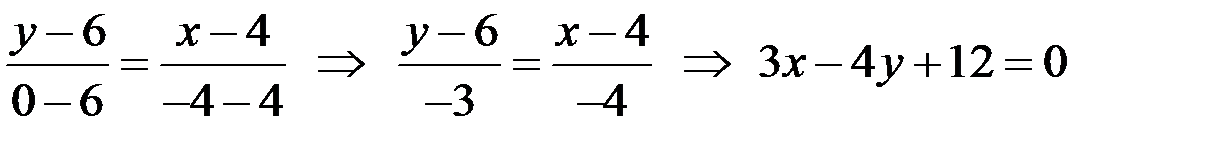- общее уравнение прямой АВ, из которого находим уравнение прямой с угловым коэффициентом , .

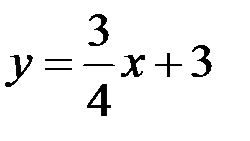2) Медиана, проведенная из вершины С делит противолежащую сторону АВ треугольника пополам. Найдем координаты точки Е середины стороны 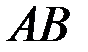(рис.1):

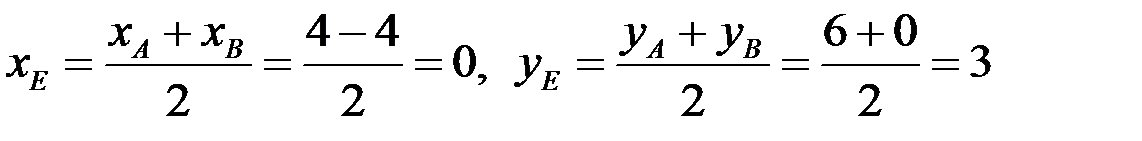, т.е. 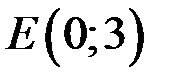, . Подставим координаты точек в уравнение прямой, проходящей через две точки, получим 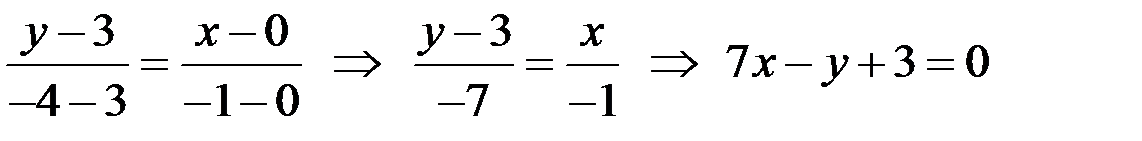- общее уравнение прямой СЕ.

3) Точка М делит каждую медиану в отношении 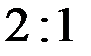, считая от вершины. Таким образом, ее координаты 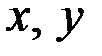можно найти по формулам:

.

В нашем случае

,

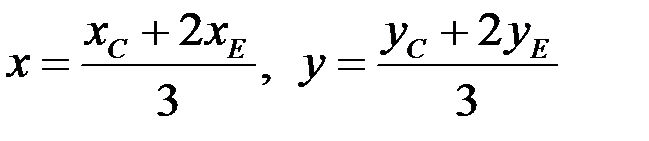откуда .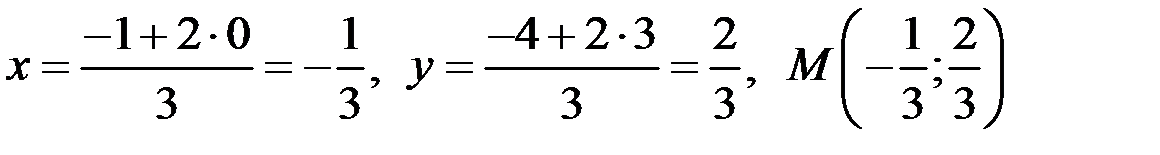

4) Найдем уравнение прямой, проходящей через заданную точку перпендикулярно прямой 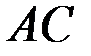из уравнения 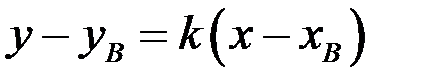. Найдем угловой коэффициент прямой АС, используя уравнение прямой, проходящей через две точк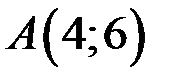и и :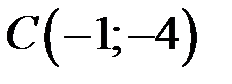

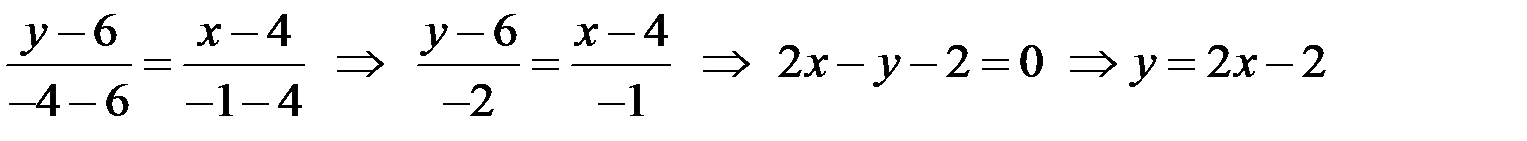- уравнение АС.

Угловой коэффициент прямой АС равен 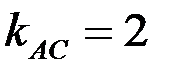, тогда, используя условие перпендикулярности двух прямых , получим

- уравнение высоты.

Длину высоты можно найти, как расстояние от точки 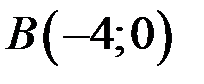до прямой АС по формуле 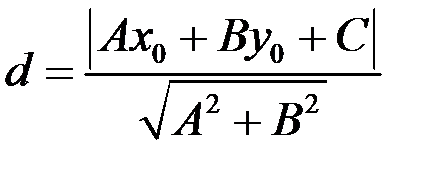. В нашем случае уравнение прямой АС: 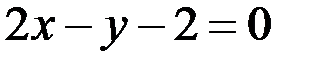, следовательно,

.

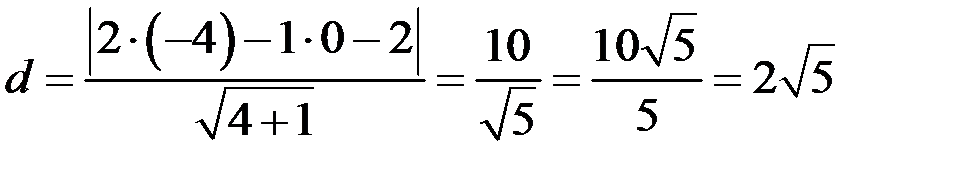5) Для нахождения уравнения прямой, проходящей через точку С параллельно прямой АВ используем уравнение прямой, проходящей через заданную точку в заданном направлении 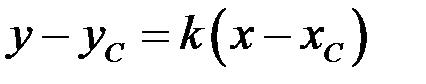и условие параллельности двух прямых. Известно, что угловой коэффициент прямой АВ равен 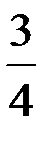, следовательно,

-

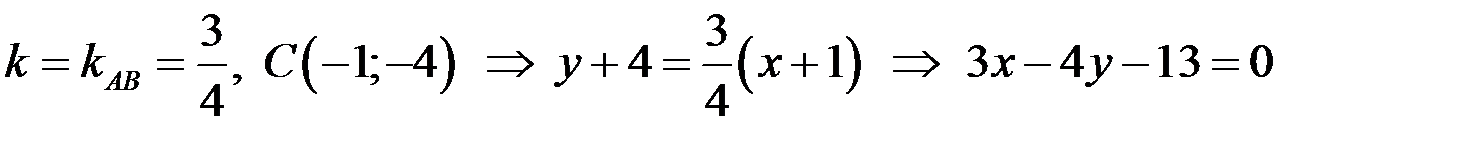- уравнение искомой прямой.

6) Площадь треугольника находится по формуле: 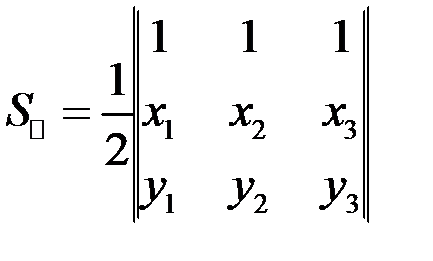, в нашем случае

.

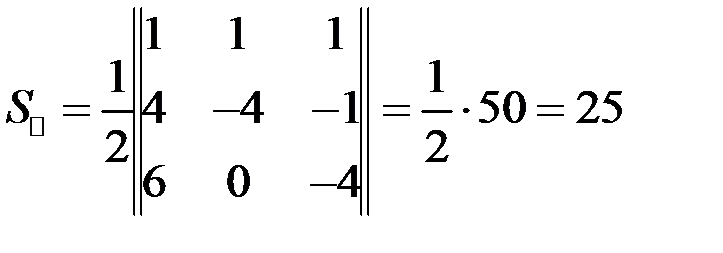у А (4;6)

Е

В (-4;0) М

0 1 х

С (-1;-4)

Рис. 1

Векторные величины (векторы) – это такие величины, которые характеризуются не только своими числовыми значениями, но и направлением.

Для изображения векторных величин служат геометрические векторы. Геометрический вектор – это направленный отрезок.

Координатами вектора в прямоугольной системе координат 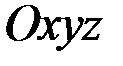называются проекции 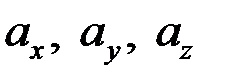вектора на оси координат. Запись 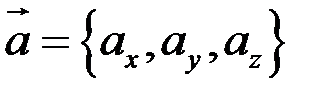означает, что вектор имеет координаты .

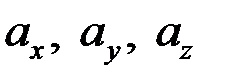Модуль вектора (его длина) вычисляется по формуле

.

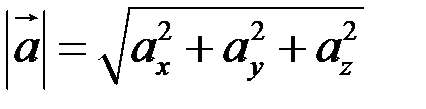Чтобы найти координаты вектора, заданного координатами точек его начала и конца надо найти разности соответствующих координат его конца и начала, т.е. если задан вектор 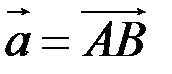, где , то

.

Тогда модуль вектора 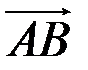находится по формуле

.

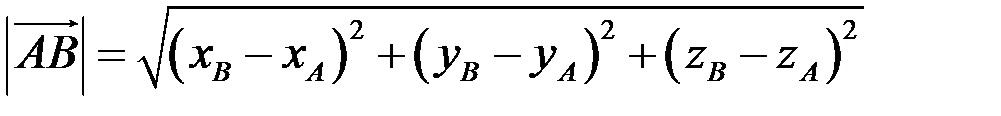Скалярным произведением двух векторов называется число, равное произведению их модулей на косинус угла между ними.

Обозначают: (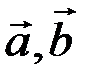) или 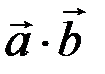. По определению

, где .

Пусть векторы заданы аналитически:

.

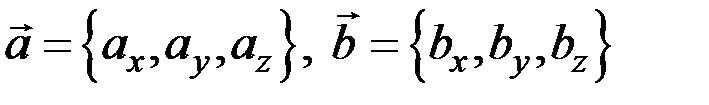Выражение скалярного произведения через координаты перемноженных векторов:

.

Косинус угла между двумя векторами можно найти по формуле

.

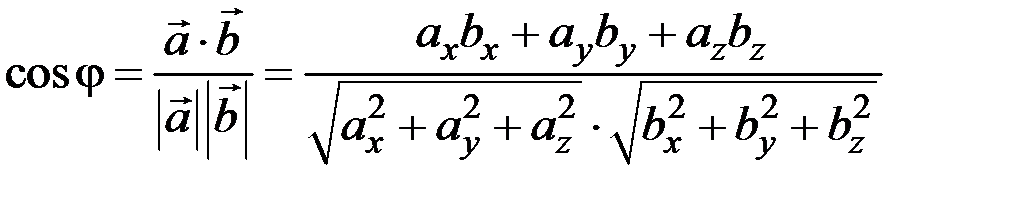Векторным произведением вектора 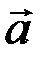на вектор 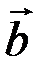называется вектор, обозначаемый символом 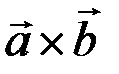или , определяемый условиями:

1) модуль этого вектора равен произведению модулей перемножаемых векторов на синус угла между ними, т.е.

;

2) этот вектор перпендикулярен каждому из перемножаемых векторов, т.е. плоскости, определяемой этими векторами;

3) направлен по перпендикуляру к этой плоскости так, что векторы и составляют правую тройку (т.е. если при наблюдении с конца вектора 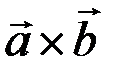кратчайший поворот от вектора 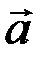к вектору 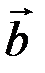происходит против часовой стрелки.)

Модуль векторного произведения численно равен площади параллелограмма, построенного на векторах сомножителях – в этом состоит геометрический смысл модуля векторного произведения:

.

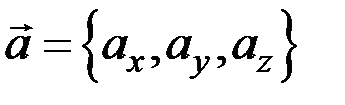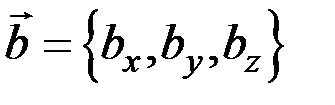Пусть даны два вектора и . Выражение векторного произведения через координаты перемножаемых векторов:

.

Смешанным произведением трех векторов 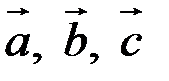называется число, равное скалярному произведению вектора 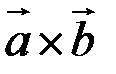на вектор 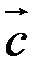, т.е. .

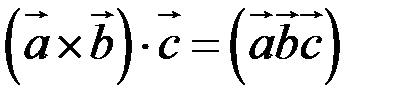Если векторы заданы своими прямоугольными координатами 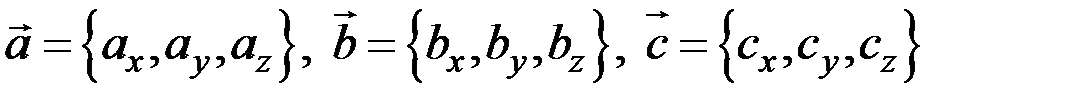, то их смешанное произведение вычисляется по формуле

.

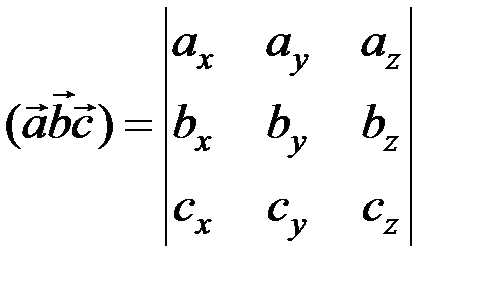Геометрический смысл смешанного произведения: объем параллелепипеда, построенного на 3-х некомпланарных векторах, равен абсолютной величине их смешанного произведения

.

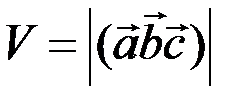Тогда объем треугольной пирамиды, построенной на этих же векторах, находится по формуле

.

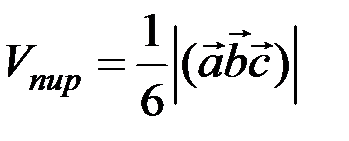Три точки пространства, не лежащие на одной прямой, определяют единственную плоскость. Если 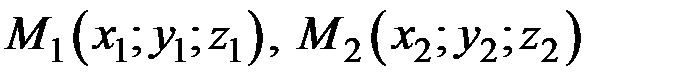, три данные точки, не лежащие на одной прямой, а 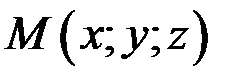произвольная точка плоскости, то уравнение плоскости, проходящей через три точки, имеет вид

.

Уравнение прямой, проходящей через две точки пространства 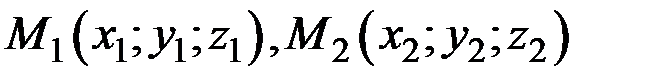имеет вид

.

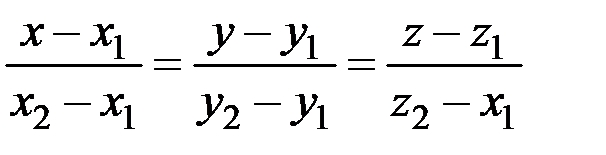Угол между прямой и плоскостью находится по формуле

,

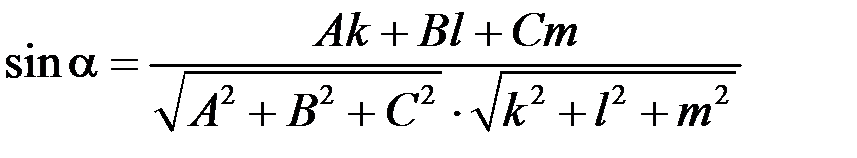где коэффициенты выбирают из канонических уравнений прямой

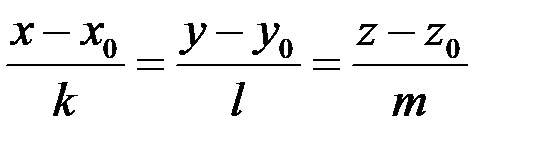
и общего уравнения плоскости

,

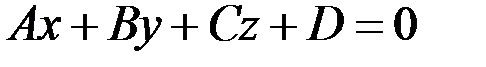где 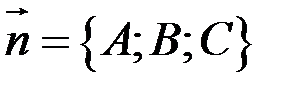- вектор нормали к плоскости.

Условие перпендикулярности прямой и плоскости:

.

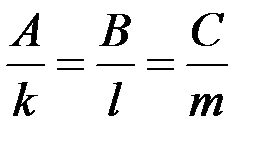Дата добавления: 2014-11-16