Поиск значения части

Варианты значений частей целого

Порядок сложения чисел

1. Учебник, ч. 3, с. 17. Упр. 1.

2. Учебник, ч. 3, с. 17. Упр. 2. Учитель высказывает мнение, что необходимо выполнить ручное измерение длины за­данной меркой. Но обнаруживается, что искомая вели­чина состоит из тех же частей, что и первая, это то же са­мое целое, но в нем части поменяли местами.

3.Учебник, ч. 3, с. 18. Упр. 3. Объяснение решений должно быть примерно таким: сложили те же части, но в другом порядке, получится то же самое целое.

4. Учебник, ч. 3, с. 18. Упр 4. Выясняется, что нужно узнать значение целого, состоящего из двух частей. Выбирают­ся два правильных действия: 8 + 3 и 3 + 8.

Предлагается одним учащимся выполнить на числовой пря­мой первый способ, а другим — второй. Результат получается тем же, однако второй способ действия занимает больше вре­мени, при этом некоторые дети могут сбиться, присчитывая число 8. Подчеркивается, что удобнее присчитывать к больше­му числу меньшее.

5. Учебник, ч. 3, с. 18. Упр. 5. Выясняется, что вторая запись не подходит ни к одному из рисунков, а две другие могут быть отнесены к любому из них.

1. На доске изображения двух корзин. В них «кладутся» апельсины-картинки. Учитель записывает поясняющие данные:

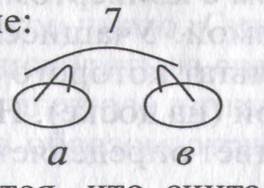
Сообщается, что считали апельсины штуками. Известно, что всего их... (7 штук). Однако неизвестно, как они разложе­ны по корзинам, и поэтому числа пока обозначены буквами. Предлагается выполнить все возможные сравнения. Выясня­ется, что легко можно сравнить число 7 с числами а и в, так как целое, конечно, больше каждой своей части, но отношение ча­стей неизвестно. С помощью числовой прямой определяются варианты разных отношений, например: 3<4, 5>2, 1<6.

2. Учебник, ч. 3, с. 19. Упр. 1.

3. Учебник, ч. 3, с. 19. Упр. 3 (упр. 2 лучше выполнить после упр. З). Содержание рисунка переносится на чертеж. При опоре на него выполняются требуемые сравнения и оп­ределяются результаты сложения и вычитания.

4. Учебник, ч. 3, с. 19, 20. Упр. 2, 4. После выполнения упр. 2 подчеркивается, как полезно знать части числа — тогда легко находить значения выражений, даже если числа не совсем знакомы.

5.Учебник, ч. 3, с. 20. Упр. 4. Даны фигуры. Предлагается с помощью штриховки показать 2 разных варианта разбие­ния на части группы, состоящей из пяти фигур. При этом учитель заранее определяет отношение частей: «Сделайте так, чтобы часть слева была больше (меньше); чтобы ча­сти были равными». Вариант частей 2 и 3 признается та­ким же, как вариант 3 и 2. Отмечается, что 5 фигур нельзя разбить на две равные части. Дополняются записи.

6. Учитель демонстрирует 2 группы картинок, которые пересчитываются. Получилось, например, 6 маков и 5 ро­машек. Все картинки складываются в конверт. Как уз­нать с помощью числовой прямой, сколько всего карти­нок в конверте? На доске рядом с конвертом учитель по­мещает отрезок числовой прямой. Учащиеся сообщают способ сложения (6 + 5), результат которого определяет­ся с помощью числовой прямой (на доске). Называется и записывается вариант 5 + 6. Ответ определяется без обра­щения к числовому ряду.

Далее учитель вынимает из конверта и выставляет на доске 3 мака и 2 ромашки (т. е. число 5 представлено разнородными объектами, но пока не определяется общее число вынутых картинок). Сколько цветов осталось в конверте? Дети, скорее всего, не смогут ответить. Нужно предложить им воспользо­ваться числовой прямой, на которой части выделены дугами. Записывается равенство: 11—5 = 6.

Вновь все картинки убираются в конверт, а затем вынима­ются и выставляются 3 мака и 3 ромашки. «Сколько фигур в конверте?». После обращения к числовой прямой делается за­пись: 11—6 = 5.

7. Учебник, ч. 3, с. 21. Упр. 5 аналогично только что опи­санному упражнению. Однако ответ теперь нужно дать уже без обращения к числовой прямой.

8. Учебник, ч. 3, с. 21. Упр. 6, 7.

9. Предлагается приступить к изучению состава числа 6.

К доске вызываются 3 ученика: один будет контролировать целое, а два других — части. Выставляются 6 картинок или фи­гур. Выделяется самая маленькая часть — ученик отодвигает одну фигуру от остальных. Учитель просит каждого из трех учеников показать свои фигуры.

На тренировочной странице учебника (с.51) на числовой прямой дано число 6. Учащиеся выделяют, проведя цветным карандашом по прямой, самую маленькую часть — длину одного шага. Тем самым обнаружится и вторая часть. Дети называют ее. «Хозяину» первой части предлагается увели­чить ее.

Учитель «стремится помочь» ему и подает «постороннюю» картинку. «Хозяин» целого возражает: тогда получится не шесть, а другое число. Оказывается, увеличение первой части должно происходить за счет второй. На числовой прямой дети продлевают цветную линию еще на один шаг.

Таким же образом отрабатываются варианты 3 + 3, 4 + 2, 5+1.

Затем все варианты записываются по порядку в виде ра­венств.

Проводится тренировка: кому удалось запомнить состав числа 6 и соответствующие случаи сложения и вычитания.

Другие упражнения на тренировочных страницах частично выполняются на этом же занятии, частично распределяются на другие.

Примерно в таком же порядке постепенно осваивается со­став других чисел первого десятка.

Следующие уроки целесообразно начинать с устного счета, в котором отрабатывается как ранее пройденный материал (прибавление и вычитание чисел 1, 2, 3), так и новый, связан­ный с изучением состава чисел.

1. Учебник, ч. 3, с. 22. Упр. 1.

2. На столе два сосуда с водой. На доске записана схема с лучами. По записи понятно, что в первом сосуде 4 ба­ночки воды, а в двух —11. Выясняется, что воду во вто­ром сосуде можно померить, но можно определить ее объем, действуя не с водой, а с числами на числовой прямой.

Но чтобы работать на ней, нужно знать, большее или мень­шее число мы ищем. Оказывается, это число обязательно меньше, чем число 11, на 4. Обсуждается и записывается реше­ние. Полученное с помощью числового ряда число проверяет­ся путем ручного измерения.

Сообщается, что действие поиска меньшего числа называ­ют вычитанием.

3. Учебник, ч. 3, с. 22. Упр. 2. Анализируя рисунок, учащи­еся рассказывают, о чем идет речь, что уже промерено, а что нужно узнать. Учитель предлагает сравнить неизвест­ное число с числом 7 — значением другой части. Оказы­вается, пока трудно сказать, какая часть больше и на сколько. Но сравнить неизвестную часть с целым можно. Выбирается решение, находится ответ.

4. Учебник, ч. 3, с. 23. Упр. 3. Как узнать, в каких случаях узнавали часть, а в каких целое? Для этого нужно помнить, как узнают часть и как узнают целое. Учащиеся формулируют соответствующие правила, например: что­бы найти целое, нужно сложить части; чтобы найти часть, нужно из целого вычесть известную часть.

Для различения записей можно предложить найденное це­лое вписать карандашом, а часть — ручкой.

5. На доске 8 и 5 яблок (картинки стоят в пачках рядом с числами). Требуется узнать целое. Уточняется, что мерой является штука. Выясняется и выполняется (с помощью числового ряда на линейке) решение. Учитель сетует, что по числовому ряду трудно делать много шагов, и знако­мит детей с калькулятором. Важно разъяснить, что каль­кулятор может выполнить и вычитание, и сложение, од­нако сам он не может выбрать действия — это работа для человека, а машинка только подсчитывает. Полученный на калькуляторе ответ оказывается тем же, что был опре­делен с помощью линейки, — это нужно обязательно продемонстрировать, чтобы показать надежность работы калькулятора.

6. Учебник, ч. 3, с. 23. Упр. 4.

7. Учебник, ч. 3, с. 23. Упр. 5 направлено на дифференциро­вание случаев поиска целого и части.

Сравниваются два верхних чертежа. Чем они различаются? Учащиеся говорят об использовании в них разных чисел. Учи­тель подводит детей к другому отличию: на одном чертеже не­известно целое, на другом — часть.

Предлагается поупражняться в поисках значения целого и части.

У. Какие действия нам известны?

Д. Сложение и вычитание.

У. Покажите жестом знак сложения... вычитания.

Дети поднимают скрещенные пальцы или один выпрямлен­ный палец. Далее этот жест используется, когда нужно пока­зать учителю выбранное действие. Результат действий может быть найден с помощью кальку­лятора.

В случае со сказочными числами на месте ответа записыва­ется вопросительный знак. В последнем задании — «ловушка»: целое меньше части. Предлагается исправить число 15 на 5, после чего записать решение.

8. Учебник, ч. 3, с. 24. Упр. 6 продолжает работу по диффе­ренцированию случаев поиска части и целого, а также готовит учащихся к решению текстовых задач.

В детский сад привезли игрушки в коробках. Имеются записи о них. Нужно определить неизвестное число, вы­полнив действие — сложение или вычитание. К первому рисунку составляется сюжет, который начинает учитель, а дети продолжают: «5 детский сад привезли пирамидки и кубики, всего... (16 штук). Пирамидок было... (7 штук). Что неизвестно? Что нужно узнать?» (Сколько привезли куби­ков?)

Неизвестное число сравнивается с имеющимися и выбира­ется действие вычитания, так как нужно найти часть.

Таким же образом составляются сюжеты по другим рисун­кам. Заметим, что пока не требуется составлять четкий текст задачи.

Для повышения мотивации при определении решения можно ввести персонаж, например Буратино, который очень любит выполнять сложение, а с вычитанием еще не разобрал­ся. Он предлагает условие: игрушки, число которых нужно уз­навать сложением, он будет забирать себе, а остальное могут забрать себе дети.

При выполнении задания со сказочными числами труднее определить, из какого числа нужно вычитать. Чтобы побудить детей к размышлению, учитель предлагает неверный порядок чисел в записи. После объяснения и выполнения правильной записи действия один из учеников придумывает сказочное число — ответ.

9.Учебник, ч. 3, с. 24. Упр. 7. Учитель называет числа, ис­пользованные в чертеже, и высказывает «сомнение» —смогут ли учащиеся найти результаты действий с этими незнакомыми большими числами без помощи калькулятора, используя лишь чертеж?

Дата добавления: 2014-11-16