Решение. Обратная задача теории погрешностей

Обратная задача теории погрешностей.

Решение.

Решение.

.

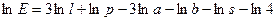Отсюда, заменяя приращения дифференциалами, будем иметь:

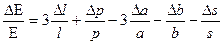. Следовательно,

.

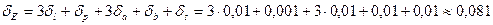Таким образом, относительная погрешность составит не более 0,081, т.е. примерно 8% от измеряемой величины.

Ответ: .

6.4. Вычислить значение величины z с помощью Mathcad при заданных значениях а, b и с с систематическим учетом абсолютных погрешностей после каждой операции, если цифры верны в строгом смысле.

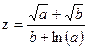, а:=12,34; b:=14,3

Алгоритм решения представлен на рисунках, приведенных ниже:

На практике очень часто необходимо уметь решать обратную задачу: каковы должны быть абсолютные погрешности аргументов функции, чтобы абсолютная погрешность функции не превышала заданной величины.

Пусть величина предельной абсолютной погрешности 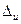задана.

Тогда .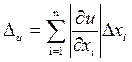

Предполагая, что все слагаемые равны между собой, будем иметь:

.

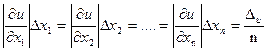Отсюда .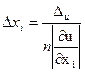

В случае, когда предельная абсолютная погрешность всех аргументов 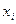одна и та же, то:

; .

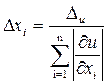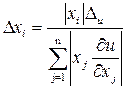7.1. Радиус основания цилиндра 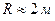; высота цилиндра 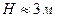. С какими абсолютными погрешностями нужно определить R и Н, чтобы объем цилиндра V можно было вычислить с точностью до 0,1 м ?

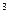Объем вычисляется по формуле 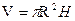и 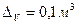. Подставляя все исходные данные, приближенно получим:

; ; .

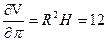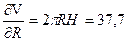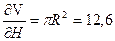Отсюда, т. к. п = 3, то, воспользовавшись формулой для вычисления погреш­ности функции, зависящей от трех переменных:

,

Будем иметь:

; ;

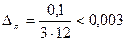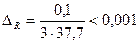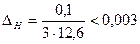
Таблица Погрешности значений элементарных функций.

8. Задания к лабораторной работе № 1:

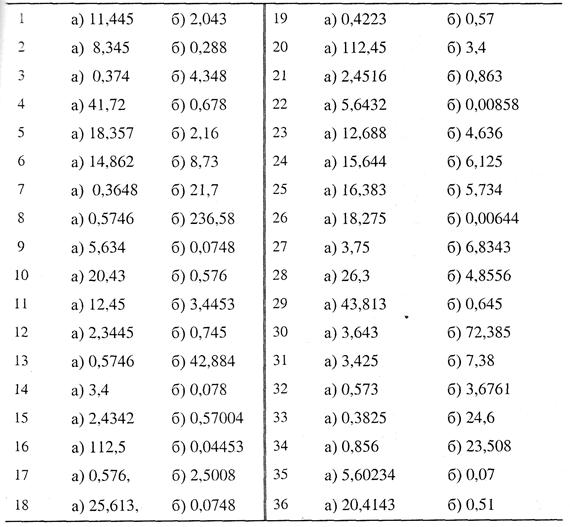
8.1. Задания (самостоятельно).Найти предельные абсолютные и относительные погрешности чисел, если они имеют только верные цифры (таблица вариантов задания).

а) в строгом смысле; б) в широком смысле.

Таблица. Варианты заданий для выполнения самостоятельной работы

8.2. Задание для самостоятельной работы. Число х (табл.), все цифры которого верны в строгом смысле, округлить до трех значащих цифр. Для полученного результата 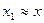вычислить границы абсолютной и относительной погрешностей. В записи числа 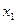, указать количество верных цифр по абсолютной и относительной погрешности.

Таблица. Варианты заданий для выполнения самостоятельной работы

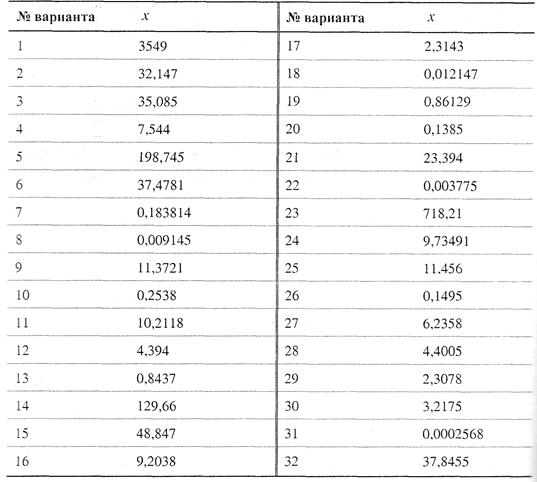
8.3. Вычислить значение величины z (табл) при заданных значениях чисел а, b и с используя систематический учет абсолютных погрешностей после каждой операции, а также с помощью метода границ. Найти абсолютную и относительную погрешности z и определить по ним количество верных цифр в z, если цифры а, b и с верны в строгом смысле.

Таблица. Варианты заданий для выполнения самостоятельной работы

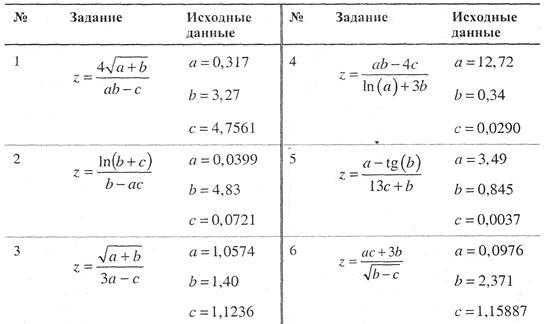
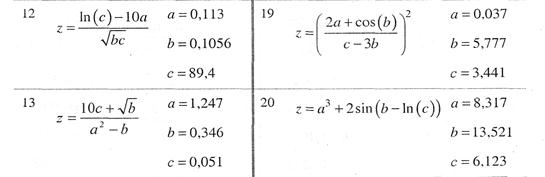
8.4. Решить следующие задачи, используя метод границ.

8.4.1. Длина воздушной трассы между двумя пунктами равна S км. Самолет преодолевает это расстояние за время t ч. Определить границы средней скорости самолета, если: ; .

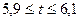8.4.2. Электроплитка рассчитана на напряжение 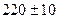В. Найти сопротивление спирали электроплитки, если известно, что через нее должен пройти ток 5±0,1 А.

8.4.3. Медный брусок имеет объем V м 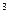(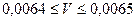). Найти его массу, если плотность меди 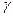кг/м 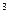составляет .

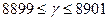8.5. Решить следующие задачи, используя общую формулу погрешности.

8.5.1. Удельное электрическое сопротивление 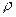металла круглого провода длиной l м с поперечным сечением d мм и сопротивлением R Ом определяется по формуле: . Найти 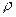, если: l=12,50 ±0,01 м, d=2,00±0,01 мм, R=0,068±0,0005 Ом, =3,141 ±0,001. Определить относительную погрешность .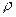

8.5.2. Вертикальный цилиндрический резервуар наполнен жидкостью. Определить время, необходимое для опорожнения резервуара через круглое отверстие в дне. Диаметр резервуара D=1±0,01м, высота уровня жидкости H=2±0,02м, диаметр отверстия дна d=0,03±0,001м, коэффициент расхода 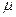=0,6 ±0,02. Расчет (в секундах) ведется по формуле: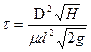

8.6. Решить следующие задачи, используя обратную задачу теории погрешностей:

8.6.1. С какой точностью надо измерить радиус круга R = 30,5 см и каким количеством значащих цифр следует ограничиться для числа , чтобы площадь круга была известна с точностью до 0,1%?

8.6.2. Длина сторон прямоугольника равны 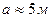, . Какова допус­тимая предельная абсолютная погрешность при измерении этих величин одинаковая для обеих сторон, чтобы площадь S прямоугольника можно было определить с предельной абсолютной погрешностью ?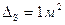

Дата добавления: 2014-11-18