Теорема умножения вероятностей n событий

Теоремы умножения вероятностей событий

Вероятность произведения двух событий равна произведе­нию вероятности одного из них на условную вероятность другого при условии, что первое событие произошло:

Р(АВ) = Р(А)· Р(В/А), Р(АВ) = Р(В) · Р(А/В).

Событие В не зависит от события А, если Р(В/А) = Р(В), т.е. вероятность события В не зависит от того, произошло ли со­бытие А. В этом случае и событие А не зависит от события В, т.е. свойство независимости событий является взаимным.

Отметим, что если А и В независимы, то независимы и 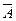и B, A и 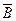, 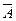и .

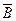Теорема умножения вероятностей независимых событий

Вероятность произведения двух независимых событий рав­на произведению их вероятностей:

Р(АВ) = Р(А)-Р(В).

Вероятность произведения n зависимых событий равна про­изведению одного из них на условные вероятности всех осталь­ных, вычисленные в предположении, что все предыдущие собы­тия наступили:

Р(А_хА₂...А_n) = Р(А₁)Р(А₂/А₁)Р(А₃/А₁А₂)...Р(А_n/А₁А₂...А_n-1)

Для трех событий А, В, С рассматриваемая выше формула примет вид Р(АВС) = Р(А)Р(В/A)P(C/AB).

События А₁,А₂,...,А_n называются независимыми в совокуп­ности, или независимыми, если они попарно-независимы, а также независимы каждое из них и произведение k остальных (k = 2,3,... n -1). Следует иметь в виду, что

- Из попарной независимости событий не следует их неза­висимость в совокупности.

- Если события А₁,А₂,...,А_n независимы, то противопо­ложные им события 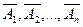также независимы.

Дата добавления: 2014-11-20