Теорема умножения вероятностей n независимых событий

Если А₁,А₂,...,А_n независимы, то вероятность их произве­дения равна произведению вероятностей этих событий:

Р(А₁,А₂,...,А_n) = Р(А₁)Р(А₂)...Р(А_n).

Замечания. 1. Равенство Р(А₁,А₂,...,А_n) = Р(А₁)Р(А₂)...Р(А_n) выражает необходимое и достаточное условие независимости со­бытий А₁,А₂,...,А_n.

2. Для трех независимых событий А, В, С рассматриваемая выше формула принимает вид

Р(АВС) = Р(А)Р(В)Р(С).

3. Вычисление вероятности суммы событий можно свести к вычислению вероятности противоположных событий по формуле

.

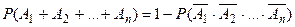В частности, если события А₁,А₂,...,А_n независимы, то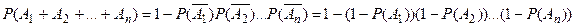

или .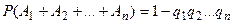

4. Если независимые события А₁,А₂,...,А_n имеют одинако­вую вероятность, равную р, то вероятность появления хотя бы одного из этих событий выражается формулой

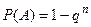, где A=А₁+А₂+..+А_n.

В обратной задаче вероятность Р(А) известна и нужно оп­ределить, при каком числе n независимых событий А_i, достигает­ся заданное значение Р(А). Если задается некоторое положитель­ное число Q, такое, что 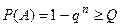, то из этого неравенства определяется значение n.

Пример 8. Подбрасываются два игральных кубика. Найти вероятность события А, состоящего в том, что - «сумма выпавших очков не превосходит четырех».

Решение. Событие А - событие, состоящее в том, что есть сумма трех несовместных событий В₂, В₃, В₄. Тогда сумма очков равна соответственно 2, 3, 4. Поскольку 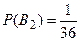, , 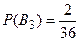, 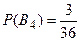по теореме сложения вероятностей несовместных событий получим

.

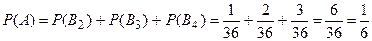Замечание. Этот же результат можно было получить, используя непосредственный подсчет вероятности. Действительно, событию А благоприятствуют 6 элементарных исходов: (1,1), (1,2), (2,1), (1,3), (3,1), (2,2). Всего же элементарных исходов, об­разующих полную группу событий, n = 36, поэтому .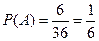

Пример 9. Три станка работают независимо. Вероятность того, что в течение смены станок (любой) потребует наладки рав­на 0,1. Найти вероятность того, что в течение смены хотя бы один станок из трех потребует внимания наладчика.

Решение. Пусть А_k - событие, заключающееся в том, что k- тый по счету станок потребует наладки в течение смены (k = 1, 2,3). Тогда событие А₁ + А₂ + А₃ заключается в том, что в течение смены наладки потребует хотя бы один из трех станков. Сначала вычислим вероятность противоположного события 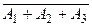, заключающегося в том, что все три станка всю смену проработают безотказно. Поскольку 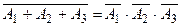, при­чем события 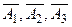независимы, то по теореме умножения вероятностей для независимых событий. По условию Р(А_k)= 0,1, тогда вероятность противоположного события 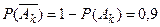. Итак, и искомая вероятность события будет .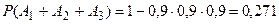

Пример 10. Имеются две урны с шариками трех цветов. В первой находятся 2 голубых, 3 красных, 5 зеленых, а во второй - 4 голубых, 2 красных и 4 зеленых. Из каждой урны извлекают по одному шару и сравнивают их цвета. Найти вероятность того, что цвета вынутых шаров одинаковы (событие А).

Решение. Обозначим событие, состоящее в извлечении из первой урны голубого шара, через В₁, красного - С₁, зеленого - D₁. Аналогичные события для второй урны обозначим соответст­венно через В₂, С₂, D₂. Событие А наступает в случае В₁В₂, С₁С₂ или D₁D₂. Они несовместны. Для вычисления искомой ве­роятности события А применим формулы вероятностей суммы несовместных событий и произведения независимых событий

Р(А) = P(B₁B₂+C₁C₂ + D₁D₂) = Р(В₁В₂) + Р(С₁С₂) + P(D₁D₂).

Так как независимы события: В₁ и В₂, С₁ и С₂, D₁ и D₂, то можно пользоваться формулой Р(АВ)= Р(А)Р(В) для каждой пары событий:

Р(В₁В₂) = Р(В₁)Р{В₂),

Р(С₁С₂) = Р(С₁)Р(С₂),

P(D₁D₂) = P(D₁)P(D₂).

Окончательно

Р(А) = Р(В₁)Р(В₂) + Р(С₁)Р(С₂) + P(D₁)P(D₂) = 0,2 · 0,4 + 0,3 · 0,2 + 0,5 · 0,4 = 0,34

Пример 11. Сколько раз нужно подбросить два игральных кубика, чтобы вероятность выпадения хотя бы один раз двух шес­терок была бы больше ? (Эта задача впервые поставлена французским математиком и писателем де Мере (1610-1684 гг.), поэтому задача называется его именем).

Решение. Пусть событие А_i - «выпадение двух шестерок при i -м подбрасывании». Так как с каждой из шести граней перво­го кубика может выпасть любая из шести граней второго кубика,
то всего равновозможных попарно несовместных событий 6 · 6 = 36. Только одно из них - выпадение шестерки и на первом и на втором кубике - благоприятствуют событию A_i. Следовательно, 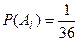, откуда .

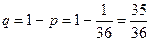Подбрасывание игральных кубиков - независимые испыта­ния, поэтому воспользуемся формулой 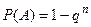, тогда в дан­ном случае получим:

, или .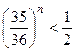

Решив неравенство, найдем п.

Логарифмируя обе части неравенства, получим 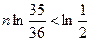, откуда .

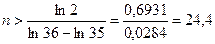Итак, чтобы вероятность выпадения двух шестерок была больше , достаточно подбросить кубик не менее 25 раз.

Пример 12. Слово папаха составлено из букв разрезной аз­буки. Карточки с буквами тщательно перемешаны. Четыре кар­точки извлекаются по очереди и раскладываются в ряд. Какова вероятность получить при этом слово папа?

Решение. Обозначим через А, В, С, D соответственно собы­тия, состоящие в том, что: извлечена первая, вторая, третья и чет­вертая буква слова папа из набора в 6 букв: а, а, а, п, п, х. Найдем вероятности событий: А, В/А, С/АВ, D/ABC.

;

;

;

.

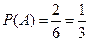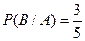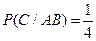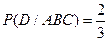В соответствии с формулой вероятности произведения зави­симых событий при п= 4будем иметь:

P(ABCD) = Р(А)Р(В/ А)Р(С / AB)P(D/ ABC) = .

Дата добавления: 2014-11-20