
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теория вероятностей и математическая статистика. И математической статистике
|
|
|
|
Павлидис. В.Д.
И математической статистике
Практикум по теории вероятностей
УДК 517
ББК 22.11
Рецензенты:
………… - доктор технических наук, профессор
С.Е. Тычинина – кандидат физико-математических наук, доцент
Практикум по теории вероятностей и математической статистике / В.Д. Павлидис
Учебное пособие содержит теоретический материал по разделам теории вероятностей, математической статистике, теории корреляции; подробное решение большого числа типовых задач и варианты типовых расчетов по данным разделам. Помимо этого в нем содержатся практические рекомендации по проведению математической обработки статистических наблюдений, оригинальный справочный материал по применению статистических критериев.
Пособие предназначено для студентов инженерных специальностей: «Механизация сельского хозяйства»-110301, «Технология обслуживания и ремонта машин в АПК»- 110304, «Электрификация и автоматизация сельского хозяйства» – 11.03.02. Оно соответствует Государственному образовательному стандарту по математике для указанных специальностей и может быть использовано как для аудиторной, так и для самостоятельной работы студентов.
Содержание
Теоретический материал и методические рекомендации
1. Краткие сведения из комбинаторики
Комбинаторика изучает способы подсчета числа элементов в конечных множествах. Формулы комбинаторики используются при непосредственном вычислении вероятностей.
Приведем некоторые сведения.
Соединениями называют различные группы предметов, составленные из каких-либо объектов.
Элементами называются объекты, из которых составлены соединения. Рассмотрим следующие три вида соединений: перестановки, размещения и сочетания.
Перестановками из n элементов называют соединения, содержащие все n элементов и отличающиеся между собой лишь порядком элементов.
Число перестановок из n элементов находится по формуле
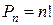 ,
,
где п! - произведение натуральных чисел от 1 до n включительно, т.е. n!=1·2·3·...·n.
Например, Р6 = 6!= 1 · 2 · 3 · 4 · 5 · 6 = 720.
Размещениями из n элементов по k в каждом (п ≥ k) называются такие соединения, в каждый из которых входит k элементов, взятых из данных n элементов, и отличающихся друг от друга либо самими элементами, либо порядком их расположения.
Число размещений из n элементов по k находят по формуле
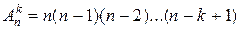 или,
или,
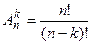
Например,

Сочетаниями из n элементов по k (п>k) называют соеди  нения, в каждый из которых входит k элементов, взятых из данных n элементов и отличающихся друг от друга, по крайней мере, одним элементом. Число сочетаний из n элементов по k находят по формуле:
нения, в каждый из которых входит k элементов, взятых из данных n элементов и отличающихся друг от друга, по крайней мере, одним элементом. Число сочетаний из n элементов по k находят по формуле:
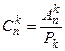 или
или
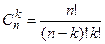 .
.
Для упрощения вычислений при 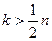 полезно использовать следующее свойство сочетаний:
полезно использовать следующее свойство сочетаний:
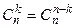 .
.
Замечания:
1) по определению 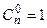 ;
;
2) для определения числа сочетаний справедливы равенства
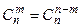 ,
, 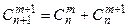 ,
, 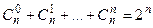
3) В записанных выше формулах комбинаторики предполагалось, что все n элементов различны. Если же некоторые элементы в соединениях повторяются, то в этом случае соединения с повторениями вычисляются по другим формулам.
Пусть среди n элементов рассматриваемого множества есть n 1 элементов одного вида, п2 элементов другого вида и т.д. Число перестановок с повторениями определяется по формуле
 ,
,
где 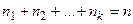 .
.
Число размещений по т элементов с повторениями из n элементов равно пт, т.е. 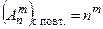 .
.
Число сочетаний с повторениями из n элементов по т элементов равно числу сочетаний без повторений из (n+m-1) элементов по т, т.е.
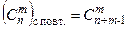
4) При решении задач комбинаторики можно использовать следующие правила:
правило суммы. Если некоторый объект А может быть выбран из множества объектов т способами, а объект В может быть выбран n способами, то выбрать либо А, либо В можно (т + п) способами.
правило произведения. Если объект А можно выбрать из множества объектов т способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана т · n способами.
2. Классическое определение вероятности события
Вероятностью события называют отношение числа элементарных исходов, благоприятствующих данному событию, к числу всех равновозможных исходов опыта, в котором может появиться это событие. Вероятность события А обозначают через Р(А) (здесь Ρ - первая буква французского слова probability - вероятность), то есть 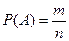 , где т — число элементарных исходов, благоприятствующих появлению события А; п - число всех равновозможных элементарных исходов опыта, образующих полную группу событий.
, где т — число элементарных исходов, благоприятствующих появлению события А; п - число всех равновозможных элементарных исходов опыта, образующих полную группу событий.
Это определение вероятности события называют классическим. Оно возникло на начальном этапе развития теории вероятностей.
Вероятность события обладает следующими свойствами:
1. Вероятность достоверного события равна единице. Обозначим достоверное событие буквой U. Для достоверного события т = n, поэтому P(U) = 1.
2. Вероятность невозможного события равна нулю. Обозначим невозможное событие буквой V. Для невозможного события m= 0, тогда P(V) = 0.
3. Вероятность случайного события выражается положительным числом, меньшим единицы. Поскольку для случайного события А выполняются неравенства 0<т<п, или 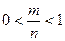 , то
, то
 0<Ρ(А)<1.
0<Ρ(А)<1.
4. Вероятность любого события В удовлетворяет неравенствам 0≤Р(В)≤1.
Пример 1. В урне 10 одинаковых по размерам и весу шаров, из которых 4 красных и 6 голубых. Из урны извлекается один шар. Какова вероятность того, что извлеченный шар окажется голубым?
Решение. Событие, состоящее в том, что «извлеченный шар оказался голубым», обозначим буквой А. Данное испытание имеет 10 равновозможных элементарных исходов, из которых 6 благоприятствуют появлению события А. По формуле классической вероятности события получим:
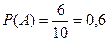 .
.
Пример 2. Все натуральные числа от 1 до 30 записаны на одинаковых карточках и помещены в урну. После тщательного перемешивания карточек из урны извлекается одна карточка. Найти вероятность того, что число на вынутой карточке окажется кратным пяти.
Решение. Обозначим через А событие, состоящее в том, что «число на вынутой карточке кратно пяти». В данном испытании имеется 30 равновозможных элементарных исходов, из которых событию А благоприятствуют 6 исходов (числа кратные пяти: 5, 10, 15, 20, 25, 30). Следовательно,
 .
.
Пример 3. Среди 25 студентов группы, в которой 10 девушек, разыгрывается 5 билетов лотереи. Найти вероятность того, что среди обладателей билетов окажутся две девушки.
Решение. Пусть А - событие, состоящее в том, что среди обладателей билетов окажутся две девушки. Найдем числа m, n.
Число всех равновозможных случаев распределения 5 билетов среди 25 студентов равно числу сочетаний из 25 элементов по 5, т.е. 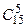 · Число групп по трое юношей из 15, которые могут получить билеты, равно
· Число групп по трое юношей из 15, которые могут получить билеты, равно 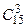 . Каждая такая тройка может сочетаться с любой парой из десяти девушек, а число таких пар равно
. Каждая такая тройка может сочетаться с любой парой из десяти девушек, а число таких пар равно 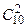 . Следовательно, число групп по 5 студентов, образованных из групп в 25 студентов, в каждую из которых будут входить трое
. Следовательно, число групп по 5 студентов, образованных из групп в 25 студентов, в каждую из которых будут входить трое
юношей и две девушки, равно произведению 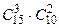 . Это произведение равно числу благоприятствующих случаев распределения пяти билетов среди студентов группы так, чтобы три билета получили юноши и два билета - девушки.
. Это произведение равно числу благоприятствующих случаев распределения пяти билетов среди студентов группы так, чтобы три билета получили юноши и два билета - девушки.
В соответствии с формулой 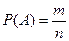 находим искомую вероятность
находим искомую вероятность
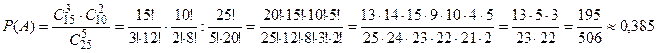
Пример 4. В ящике находятся 15 красных, 9 голубых и 6 зеленых шаров. Наудачу вынимают 6 шаров. Какова вероятность того, что оказались вынуты 1 зеленый, 2 голубых и 3 красных шара (событие А).
Решение. В ящике всего 30 шаров. При данном испытании число всех равновозможных элементарных исходов будет 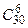 . Подсчитаем число элементарных исходов, благоприятствующих событию А. Три красных шара из 15 можно выбрать
. Подсчитаем число элементарных исходов, благоприятствующих событию А. Три красных шара из 15 можно выбрать 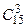 способами, два голубых шара из 9 можно выбрать
способами, два голубых шара из 9 можно выбрать 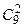 способами, один зеленый из 6 -
способами, один зеленый из 6 - 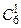 способами. Следовательно (в силу принципа произведения в комбинаторике), число исходов, благоприятствующих событию А, будет
способами. Следовательно (в силу принципа произведения в комбинаторике), число исходов, благоприятствующих событию А, будет 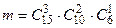 . По формуле
. По формуле 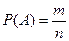 находим искомую вероятность
находим искомую вероятность
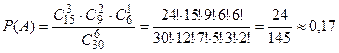 .
.




 3. Геометрические вероятности события
3. Геометрические вероятности события
Классическое определение вероятности события предполагает, что число элементарных исходов конечно. На практике же встречаются опыты, для которых множество таких исходов бесконечно.
Для преодоления недостатка классического определения вероятности, состоящего в том, что оно неприменимо к испытаниям с бесконечным числом исходов, введем понятие геометрической вероятности события.
Пусть на плоскости задана квадрируемая область, т.е. область, имеющая площадь. Обозначим эту область буквой G, а ее площадь SG. В области G содержится область g площади Sg (рис.1)
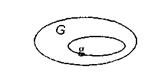
Рис. 1.
В область G наудачу брошена точка. Будем считать, что брошенная точка может попасть в некоторую часть области G с вероятностью, пропорциональной площади этой части и не зависящей от ее формы и расположения. Пусть А - событие, состоящее в том, что брошенная точка оказалась в области g, тогда геометрическая вероятность этого события определяется формулой
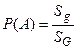 .
.
Аналогично вводится понятие геометрической вероятности при бросании точки в пространственную область G объема VG, содержащую область g объема Vg:
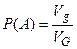
В общем случае понятие геометрической вероятности вводится следующим образом: обозначим меру области (длину, площадь, объем) через mes g, а меру области G - через mes G (mes - первые три буквы французского слова mesure, что значит мера); обозначим буквой А событие, состоящее в том, что произошло «попадание брошенной точки в области g, которая содержится в области G». Вероятность попадания в область g точки, брошенной в область G, определится формулой:
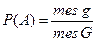 .
.
Пример 5. В круг вписан квадрат (рис.2). В круг наудачу бросается точка. Какова вероятность того, что эта точка попадет в квадрат?
Решение. Введем обозначения: R - радиус круга, а - сторона вписанного квадрата, А - событие, состоящее в том, что точка попала в квадрат, S - площадь круга, S1 - площадь вписанного квадрата. Известно, что площадь круга S = πR2. Сторона вписанного квадрата через радиус описанной окружности выражается
формулой  , поэтому площадь квадрата S1 = 2R2.
, поэтому площадь квадрата S1 = 2R2.
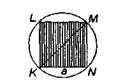
Рис. 2.
Полагая в формуле 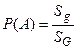 Sg= S1, SG = S, находим искомую вероятность
Sg= S1, SG = S, находим искомую вероятность 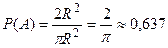 .
.
Замечание. Выражение стороны квадрата через радиус окружности можно получить следующим образом. Из треугольника D KMN по теореме Пифагора будем иметь: KN2 + NM2 = КМ2, т.е.
a2 + a2=(2R)2, 2a2=4R2, a2 =2R2,  .
.




 4. Алгебра событий
4. Алгебра событий
Суммой, или объединением двух событий называется событие, состоящее в появлении хотя бы одного из этих событий. Сумма двух событий А и В обозначается через А + В или 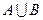 . Аналогично определяется и обозначается сумма n событий - событие, состоящее в появлении хотя бы одного из событий. Сумму n событий А1, А2,...,Аn обозначают так:
. Аналогично определяется и обозначается сумма n событий - событие, состоящее в появлении хотя бы одного из событий. Сумму n событий А1, А2,...,Аn обозначают так:
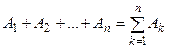 или
или 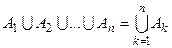 .
.
Произведением, или пересечением двух событий называется событие, состоящее в одновременном их появлении. Произведение двух событий А и В обозначается через АВ или 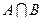 . Аналогично определяется и обозначается произведение в случае n событий А1, А2,...,Аn обозначают:
. Аналогично определяется и обозначается произведение в случае n событий А1, А2,...,Аn обозначают: 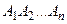 или
или 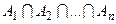 .
.
Понятия суммы и п роизведения событий распространяются и на бесконечные последовательности событий. В этих случаях используются обозначения соответственно:
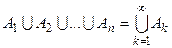 ,
,
 .
.
Если событие А обязательно произойдет при появлении некоторого другого события В, то говорят, что событие В представляет собой частный случай события А, и пишут В Ì А, или ΑÉ Β (говорят также, что В влечет А).
Если В Ì А и ΑÌ Β, т.е. события А и В в данном опыте могут появиться или не появиться вместе, то их называют равносильными, или эквивалентными, пишут А = В.
Операции объединения и пересечения событий обладают некоторыми свойствами, аналогичными свойствам сложения и умножения чисел. Эти операции
коммутативны:  ,
,  ;
;
ассоциативны:
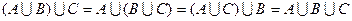 ;
;
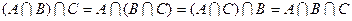 ;
;
дистрибутивны: 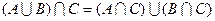 .
.
Указанные свойства следуют из определения действий объединения и пересечения событий.
Однако не все законы сложения и умножения чисел справедливы для объединения и пересечения событий. Так, для любого события А выполняются равенства
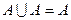 ,
, 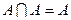 .
.
Если U— достоверное, V— невозможное событие, А — любое случайное событие, 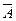 - событие, противоположное А, то выполняются следующие равенства:
- событие, противоположное А, то выполняются следующие равенства:
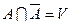 , или
, или 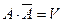 .
.
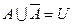 , или
, или  .
.
 , или
, или  .
.
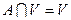 , или
, или 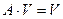 .
.
 , или
, или  .
.
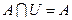 , или
, или 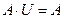 .
.
Из свойств операций пересечения и объединения следует, что для любых событий А и В имеем
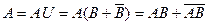 , т.е.
, т.е.
 , или
, или 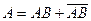 .
.
Формула  , или
, или 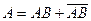 дает разложение любого события А на сумму двух непересекающихся (несовместных) событий.
дает разложение любого события А на сумму двух непересекающихся (несовместных) событий.
Если BÌA, то АВ = В и формула  , или
, или 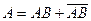 принимает вид:
принимает вид:
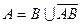 или
или 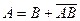 .
.
Разностью событий А и В называют событие С, которое означает, что наступает событие А и не происходит событие В. Разность событий А и В обозначается так: А-В, или А \ В.
Пример 6. Подбрасывают игральный кубик. Введем события: А - событие, состоящее в «выпадении шести очков», В - событие, состоящее в «выпадении трех очков», С - событие, состоящее в «выпадении четного числа очков», D - событие, состоящее в «выпадении числа очков, кратных трем». Каковы соотношения между этими событиями?
Решение. Если выпало шесть очков, то тем самым выпало и четное число очков, т.е. событие А влечет событие С: А Ì С. Рассуждая аналогично, получаем AÌD, В Ì D, А + B = D, C·D = A.
Пример 7. Доказать, что 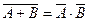 .
.
Решение. Для доказательства равенства достаточно показать, что 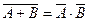 и
и  . Если наступило событие
. Если наступило событие 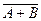 , то это означает, что произошло событие, противоположное А + В, т.е. наступили
, то это означает, что произошло событие, противоположное А + В, т.е. наступили 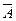 и
и 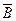 одновременно:
одновременно: 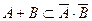 . С другой стороны, если произошло событие
. С другой стороны, если произошло событие  , то это означает, что произошло и
, то это означает, что произошло и 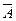 , и
, и 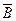 , т.е. не наступило ни одно из событий A и В:
, т.е. не наступило ни одно из событий A и В:  . Итак, поскольку
. Итак, поскольку 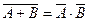 и
и  , то поопределению действий:
, то поопределению действий: 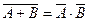 .
.
4. Основные теоремы теории вероятностей
|
|
|
|
|
Дата добавления: 2014-11-20; Просмотров: 851; Нарушение авторских прав?; Мы поможем в написании вашей работы!