Случайные величины: дискретные и непрерывные

При решении задач этого раздела рекомендуется хорошо изучить теоретический материал.

Понятие случайной величины - одно из фундаментальных в теории вероятностей. Оно тесно связано с понятием случайного события, являясь в некотором смысле его обобщением. Первич­ным здесь является испытание, но результат характеризуется не альтернативным исходом (появляется или нет событие), а некото­рым числом (например, число т появлений события в п повтор­ных испытаниях; число очков, выбиваемых стрелком; размер вклада на случайно выбранном в Сбербанке счете и т.д.). Случай­ная величина, как и случайное событие, подлежит четкому опре­делению по условию задачи. Связь со случайным событием за­ключается в том, что принятие случайной величиной некоторого числового значения (т.е. выполнение равенства X = x_i) есть слу­чайное событие, характеризуемое вероятностью Р(Х = х_i) = р_i.

Случайной величиной называют переменную величину, ко­торая в зависимости от исходов испытания принимает значения, зависящие от случая.

Случайная величина, принимающая различные значения, которые можно записать в виде конечной или бесконечной после­довательности, называется дискретной случайной величиной.

Случайная величина, которая может принимать все значе­ния из некоторого промежутка, называется непрерывной случай­ной величиной.

Случайные величины обозначают буквами латинского ал­фавита X, Y, Z..., а их значения - строчными буквами с индекса­ми, например, x₁,x₂,x₃,...

Законом распределения дискретной случайной величины на­зывается соответствие между возможными значениями x₁,x₂,x₃,... и соответствующими им вероятностями p₁,p₂,p₃,...

Закон распределения дискретной случайной величины может быть задан таблично или аналитически (т.е. с помощью формул).

Если дискретная случайная величина X принимает конечное множество значений x₁,x₂,x₃,... соответственно с вероятностями p₁,p₂,p₃,... то ее закон распределения определяется формулами: P(X = x_k) = p_k (k = 1,2,..., п), причем 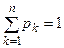. Этот закон запишем в виде таблицы

X	X1	х2	x3	…	xn
P	p1	p2	p3	…	pn

В этой таблице сумма всех вероятностей равна единице, т.е. 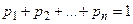. События (X – х_k), (k = 1,2,..., n), образуют полную группу событий, поэтому и выполняется равенство .

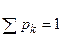Функцией распределения случайной величины X называется функция действительной переменной х, определяемая равенст­вом F(x) = P(X<x),

Р(Х < х) - вероятность того, что случайная величина X примет значения, меньше х. Геометрически это означает следующее: F(x) - вероятность того, что случайная величина X примет значение, которое изображается точкой на числовой прямой, распо­ложенной слева от точки х. (рис. 3).

Рис. 3.

Случайная величина называется непрерывной, если ее функ­ции распределения F(x) = Р(Х < х) является непрерывной и диф­ференцируемой.

Вероятность того, что случайная величина X примет значе­ние из полуинтервала [ α,β), равна разности значений ее функции распределения F(x) на концах этого полуинтервала:

P(α≤ X<β) = F(β)-F(α).

Функция распределения F(x) случайной величины X обладает следующими свойствами.

1. Все значения функции распределения F(x) принадлежат отрезку [0;l], т.е. 0 ≤ F(x) ≤ 1.

2. Функция распределения F(x) является неубывающей, т.е. если х₁ < х₂, то F(x₁) < F(x₂).

3. Функция F(x) в точке х₀ непрерывна слева, т.е. , .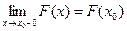

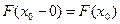4. Если все возможные значения случайной величины X при­надлежат интервалу (a;b), то для этой функции распреде­ления F(x) = 0 при х≤а, F(x) = 1при х≥b.

5. Если все возможные значения случайной величины X при­надлежат бесконечному интервалу (-∞;+∞), то , .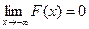

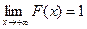6. Если X непрерывная случайная величина, то вероятность того, что она примет одно, заданное определенное значе­ние, равна нулю: Р(Х =α) = 0, поэтому выполняются равенства:

Р(α ≤ X < β) = Р(α < X ≤ β) = Р(α < X < β)

P(α<X<β) = F(β)-F(α).

Дата добавления: 2014-11-20