I. Примеры некоторых распределений дискретных слу­чайных величин

1. Биномиальное распределение

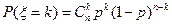, 0< p <1, k =0,1,2,…, n.

2. Распределение Пуассона

, a >0, k =0,1,2,…

3. Геометрическое распределение

, 0< p <1, k =0,1,2,…

4. Гипергеометрическое распределение

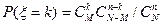, k =0,1,2,…, min(M,n).

II. Примеры некоторых распределений непрерывных случайных величин

1. Равномерное распределение

, -∞< a < b <+∞.

2. Нормальное распределение (с параметрами (а,σ))

, -∞< a < +∞, σ>0.

3. Показательное распределение

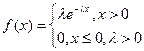
4. Распределение Коши

.

Пример 25. Сырье на завод привозят от 3-х независимо ра­ботающих поставщиков на автомашинах. Вероятность прибытия автомашины от первого поставщика равна 0,2; от второго - 0,3; от третьего - 0,1. Составить закон распределения числа прибывших машин. Найти математическое ожидание М(Х), дисперсию D(X) и среднее квадратическое отклонение σ(Х) случайной величины X. Найти функцию распределения и построить ее гра­фик.

Решение. Для нахождения числовых характеристик дис­кретной случайной величины X - числа прибывших автомашин, необходимо составить закон ее распределения, который в общем вине записывается в виде таблицы так:

X	х1	х2	…	xn
P	p1	p2	…	pn

Где х_i, - возможные значения дискретной случайной величины X, P_t = Р(Х = х_i) - вероятность того, что случайная величина X примет значение х_i, причем .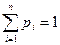

Для данного случая имеем:

хi
pi	p1	p2	p3	p4

Надо найти значения вероятностей p_i. Равенство X = 0 означает, что на завод не прибудет ни одна из трех автомашин. Следовательно: p₁= р(Х = 0) = 0,8 ·0,7 ·0,9 = 0,504 (по теореме умножениявероятностей независимых событий).

Равенство X = 1 означает, что на завод прибудет только однаиз трех автомашин. Пользуясь теоремой сложения вероятностейнесовместных событий и теоремой умножения независимых событий,найдем значение р₂:

p₂ = р(Х = 1) = 0,2 · 0,7 · 0,9 + 0,8 · 0,3 · 0,9 + 0,8 · 0,7 · 0,1 = 0,398.

Рассуждая аналогично, найдем р₃ и р₄:

р₃ = 0,2 · 0,3 · 0,9 + 0,8 · 0,3 · 0,1 + 0,2 · 0,7 · 0,1 = 0,092,

р₄ = 0,2 · 0,3 · 0,1 = 0,006.

Запишем закон распределения:

хi
pi	0,504	0,398	0,092	0,006

Для вычисления математического ожидания М(Х), дисперсии Р(Х) и среднего квадратического отклонения σ(Х) воспользуемсяформулами приведенными выше:

М(Х) = 0 · 0,504 +1 · 0,398 + 2 · 0,092 + 3 · 0,06 = 0,6,

D(X) = 0 · 0,504 +1 · 0,398 + 4 · 0,092 + 9 · 0,06 - 0,6² = 0,46,

σ(Х)= 0,678.

Найдем функцию распределения F(x) = Р(Х < х):

если х ≤ 0, то F(x) = 0,

если 0 < х ≤ 1, то F(x) = 0,504,

если 1 < х ≤ 2, то F(x) = 0,504 + 0,398 = 0,902,

если 2 < х ≤ 3, то F(x) = 0,902 + 0,092 = 0,994,

если х > 3, то F{x) = 0,994 + 0,006 = 1.

Таким образом:

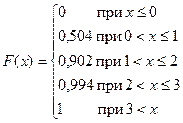
Построим график этой функции:

Рис. 4.

Пример 26. Случайная величина X задана интегральной функцией (функцией распределения) F(X). Требуется найти:

а) дифференциальную функцию (плотность вероятности);

б) математическое ожидание и дисперсию X;

в) построить графики интегральной и дифференциальной функций

.

Решение. а) между интегральной и дифференциальной функциями непрерывной случайной величины выполняется соот­ношение F'({x) = f(x). В данном случае будем иметь

б) числовые характеристики непрерывной случайной величины определяются по формулам:

,

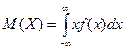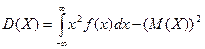
Тогда имеем

.

в) строим графики функций

Рис. 5 Рис. 6.

Пример 27. Заданы математическое ожидание а и среднее квадратическое отклонение σ нормально распределенной слу­жимой величины X: а = 8, σ = 2, α =4, β = 14, δ = 6. Требуется найти:

а) вероятность того, что X примет значение, принадлежащее интервалу (4;14);

б) вероятность того, что абсолютная величина отклонения X-a окажется меньше δ.

Решение. а) вероятность того, что нормально распределен­ная случайная величина примет значение, принадлежащее интер­валу (α; β), равна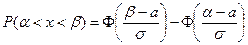

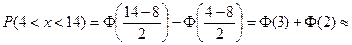(по таблице значений функции Ф(х) ≈ 0,4986+0,4772 =0,9758;

б) вероятность того, что абсолютная величина отклонения меньше положительного числа δ равна 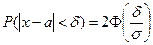. В данном случае имеем .

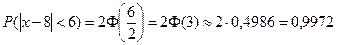Дата добавления: 2014-11-20