Генеральной совокупности по выборке

Статистическое оценивание характеристик распределения

10.1. Точечные оценки и их свойства. Метод подстановки.

Так как основная задача математической статистики состо­ит в нахождении распределения наблюдаемой случайной величи­ны X по данным выборки и во многих случаях вид распределения X можно считать известным, то задача сводится к получению приближенных значений неизвестных параметров этого распреде­ления.

Пусть F_x (x, θ) — функция распределения случайной вели­чины X, содержащая один неизвестный параметр θ, а х₁, х₂,..., х_n -выборка наблюдений этой случайной величины. Точечной оценкой 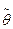неизвестного параметра θ называется приближенное значение этого параметра, полученное по выборке.

Заметим, что оценка 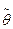есть значение некоторой функции элементов выборки, т.е. 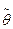= 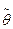(х₁, х₂,..., х_n). Любую функцию эле­ментов выборки называют статистикой. Для уточнения свойств статистики 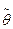(х₁, х₂,..., х_n) таких, чтобы ее значения можно считать хорошей в некотором смысле оценкой параметра θ, ее надо рас­сматривать как функцию случайного вектора (Х₁, Х₂,..., Х_n), од­ной из реализаций которого является данная выборка х₁, х₂,..., х_n. Так как закон распределения каждой из случайных величин X_i, i = 1,2,..., n, есть F_x (x, θ), являющаяся функцией параметра θ, то и распределение статистики 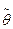(х₁, х₂,..., х_n) также зависит от неиз­вестного параметра θ.

Качество оценок характеризуется следующими основными свойствами:

а) Состоятельность. Оценка = 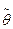(х₁, х₂,..., х_n) называ­ется состоятельной оценкой параметра θ, если 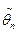сходится по вероятности к θ при n →∞. Последнее означает, что 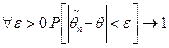при n →∞.

Состоятельность оценки 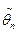вбольшинстве случаев уста­навливается с помощью следующей теоремы.

Теорема1. Есл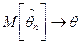и и при n →∞, то 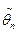— состоятельная оценка параметра θ.

б) Несмещенность. Оценка θ называется несмещенной оценкой параметра θ, если ее математическое ожидание равно оцениваемому параметру, т.е. .

Разность называется смещением. Для несмещен­ных оценок систематическая ошибка оценивания равна нулю.

Простейший метод статистического оценивания - метод подстановки или аналогии — состоит в том, что в качестве оценки той или иной числовой характеристики (среднего, дисперсии и др.) генеральной совокупности берут соответствующую характе­ристику распределения выборки - выборочную характеристику.

Пример 38. Пусть х₁, х₂,..., х_n - выборка из генеральной со­вокупности с конечными математическим ожиданием и дисперси­ей σ². Используя метод подстановки, найти оценку т. Проверить свойства несмещенности и состоятельности полученной оценки.

Решение. По методу подстановки в качестве оценки т ма­тематического ожидания возьмем математическое ожидание рас­пределения выборки - выборочное среднее. Тогда, получим

.

Для проверки несмещенности и состоятельности выбо­рочного среднего как оценки т, рассмотрим эту статистику как функцию выборочного вектора (Х₁, Х₂,..., Х_n). По определению вы­борочного вектора имеем: M[X_i]=т и D[X_i]=σ², i = 1,2,..., п, причем X_i - независимые в совокупности случайные величины.

В данном случае будем иметь

,

.

Отсюда по определению получаем, что 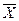- несмещенная оценка т, и так как при n →∞, то в силу теоремы 1 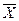является состоятельной оценкой математического ожидания т генеральной совокупности.

Пример 39. Доказать теорему о состоятельности оценки.

Доказательство: для оценки параметра θ может быть пред­ложено несколько несмещенных оценок. Мерой точности несме­щенной оценки 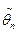считают ее дисперсию D[ ].

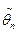Пусть 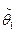и - две различные несмещенные оценки пара­метра θ. Если 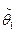D[ ]<D[ ], то говорят, что оценка 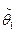более эф­фективна, чем оценка .

В предположении, что распределение случайной величины Х и статистика 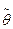удовлетворяют некоторым условиям регулярно­сти (А^*), для дисперсии несмещенной оценки 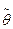параметра θ вы­полняется неравенство Крамера - Рао:

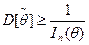, где 1_п (θ) - информация Фишера, содержащаяся в выборке объема п относительно неизвестного параметра θ. Для непрерывной случайной величины Х сплотностью распределения f_x (x, θ) .

Если же Х- дискретная случайная величина, то , где р(Х, θ) = Р[Х = х].

Условия регулярности (А^*)выполняются для обычно ис­пользуемых статистик нормального, биномиального и пуассонов-ского распределений.

Несмещенная оценка параметра θ, дисперсия которой достигает своего наименьшего возможного значения , называется эффективной: .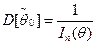

Несмещенная оценка 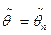называется асимптотически эффективной оценкой параметра θ, если .

Если условия регулярности (А^*) не выполняются, то может существовать несмещенная оценка параметра θ, дисперсия кото­рой меньше, чем нижняя граница в неравенстве .

Такая оценка называется сверхэффективной.

10.2. Метод максимального правдоподобия

Метод максимального правдоподобия является одним из наиболее распространенных методов нахождения оценок неиз­вестных параметров распределения генеральной совокупности. Пусть Х- непрерывная случайная величина с плотностью распре­деления f_x (x, θ), зависящей от неизвестного параметра θ, значе­ние которого требуется оценить по выборке объема п. Плотность распределения выборочного вектора (Х₁, Х₂,..., Х_n)можно записать в виде .

Пусть х₁, х₂,..., х_n - выборка наблюдений случайной величины X,по которой находится оценка неизвестного параметра.

Функцией правдоподобия L(θ) выборки объема п называет­ся плотность выборочного вектора, рассматриваемая при фикси­рованных значениях переменных х₁,...,х_п. Функция правдоподо­бия является, таким образом, функцией только неизвестного параметра θ, т.е. .

Аналогично определим функцию правдоподобия выборки дискретной случайной величины X. Пусть Х- дискретная случай­ная величина, причем вероятность Р[Х = х]= р(х, θ) есть функ­ция неизвестного параметра θ. Предполагая, что для оценки па­раметра θ получена конкретная выборка наблюдений случайной величины X объема п: х₁,...,х_п. Функция правдоподобия L(θ) вы­борки объема п равна вероятности того, что компоненты выбо­рочного вектора Х₁,...,Х_n примут фиксированные значения х₁,...,х_п, т.е. .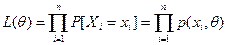

Метод максимального правдоподобия состоит в том, что в качестве оценки неизвестного параметра θ принимается значение 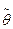, доставляющее максимум функции правдоподобия. Такую оценку называют МП - оценкой. В случае дискретного распреде­ления наблюдаемой случайной величины X МП - оценка неиз­вестного параметра θ есть такое значение 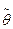, при котором веро­ятность появления данной конкретной выборки максимальна. Аналогичную интерпретацию МП - оценки дают и в случае оценки параметра распределения непрерывной случайной величины.

Для упрощения вычислений, связанных с получением МП -оценок, в некоторых случаях удобно использовать логарифмиче­скую функцию правдоподобия, т.е. ln L(θ).

При выполнении некоторых достаточно общих условий МП - оценки состоятельны, асимптотически эффективны и асимпто­тически нормально распределены. Последнее означает, что при увеличении объема выборки п для МП - оценки 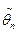неизвестного параметра θ выполняется условие .

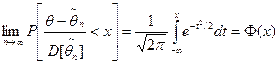Если для параметра θ существует эффективная оценка, то метод максимального правдоподобия дает именно эту оценку и другой МП - оценки не существует.

Пример 40. Найти МП - оценки математического ожидания т и дисперсии σ² нормально распределенной генеральной сово­купности.

Решение. Пусть х₁,х₂,...,х_п - выборка наблюдений случай­ной величины X с плотностью распределения

.

Найдем функцию правдоподобия L(m, σ²). Имеем

.

Логарифмическая функция правдоподобия отсюда равна

.

Используя необходимые условия максимума , по­лучим систему уравнений для нахождения искомых МП - оценок:

,

.

Из первого уравнения этой системы находим .

Подставляя полученное значение во второе уравнение, будем иметь .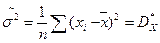

Отметим, что выборочное среднее является несмещенной и состоятельной оценкой т (см. пример 38), а также эффективной оценкой в случае нормально распределенной генеральной сово­купности (убедитесь в этом самостоятельно). Выборочная диспер­сия является состоятельной и смещенной оценкой σ².

Пример 41. Найти МП - оценку параметра X распределе­ния Пуассона.

Решение. Пусть х₁,...,х_п - выборка наблюдений случайной величины X, имеющей распределение Пуассона с неизвестным параметром X, т.е.

,

где х принимает неотрицательные целочисленные значения, х = 0,1,2. Функция правдоподобия L(λ) выборки объема п определяется так: .

Найдем логарифмическую функцию правдоподобия:

.

Используя необходимое условие экстремума, получим урав­нение для определения МП-оценки:

.

Отсюда следует, что .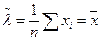

Полученная МП - оценка является несмещенной и состоя­тельной оценкой λ (пример 38), а также эффективной оценкой этого параметра.

10.3. Метод моментов

Для получения оценок неизвестных параметров θ₁,θ₂,...,θ_s распределения генеральной совокупности X используется и метод моментов. Поясним его.

Пусть f _х (х, θ₁,θ₂,...,θ_s) - плотность распределения случай­ной величины X. Определим с помощью этой плотности S каких-либо моментов случайной величины X, например, первые S на­чальных моментов, по формулам

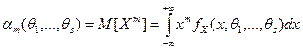, m =1,2,..., S.

По выборке наблюдений случайной величины найдем зна­чения соответствующих выборочных моментов:

, m =1,2,..., S.

Попарно приравнивая теоретические моменты α_т случай­ной величины X их выборочным значениям , получаем систему s уравнений с неизвестными θ₁,θ₂,...,θ_s:

, m =1,2,..., S.

Решая полученную систему относительно неизвестных θ₁,θ₂,...,θ_s, находим оценки неизвестных параметров.

Аналогично находятся оценки неизвестных параметров по выборке наблюдений дискретной случайной величины.

Пример 42. Методом моментов найти оценки неизвестных параметров а и b для Г - распределения с плотностью

.

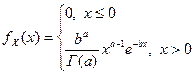Решение. Для нахождения оценок параметров а и b по мето­ду моментов воспользуемся начальным моментом первого поряд­ка (математическим ожиданием) и центральным моментом второ­го порядка (дисперсией):

, .

По выборке х₁,...,х_n из генеральной совокупности, имеющей Г-распределение, находим значения соответствующих выборочных моментов:

, .

Приравнивая соответствующие равенства, получаем сле­дующую систему уравнений:

, . Решая ее, находим , .

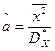10.4. Распределения χ², Стьюдента и Фишера.

Распределения основных статистик, вычисляемых по выборке из нормально распределенной генеральной совокупности, связаны с распределениями χ² (k), Стьюдента Т(к) и Фишера F(k₁,k₂).

Квантили этих распределений приведены в приложении (таблицы П5, П6, П7). Дадим определения и некоторые свойства этих рас­пределений.

а) Распределением χ² с k степенями свободы называется распределение случайной величины χ² (k), равной сумме квадра­тов k независимых нормально распределенных по закону N(0,1) случайных величин U_i, i = 1,2,..., k, т. е. распределение случайной величины .

Распределение χ² с k степенями свободы там, где это не вызывает недоразумений, будет обозначаться также χ² (k).

Плотность распределения определяется формулой

.

График функции приведен на рис. 12. Среднее и дис­персия распределения χ² (k) равны соответственно: M[χ² (k)] = k, D[χ² (k)] = 2k.

Рис. 12.

Распределение χ² часто используется в статистических рас­пределениях. Рассмотрим следующую теорему.

Теорема 2. Пусть х₁,х₂,...,х_п - выборка из нормально рас­пределенной генеральной совокупности N(m,σ), a и - соответственно выборочное среднее и выборочная дисперсия. Тогда статистики 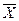и S² - независимые случайные величины, причем статистика имеет распределение χ² (n -1).

Заметим, что если χ² (k ₁) и χ² (k ₂) - независимые случай­ные величины, имеющие распределение χ² с k ₁ и k ₂степенями свободы соответственно, то сумма этих случайных величин имеет распределение χ² с (k ₁, k ₂ ) степенями свободы: χ² (k ₁)+ χ² (k ₂)= χ² (k ₁+ k ₂).

Распределение χ² (k) при больших значениях k k>30 с достаточной для практических расчетов точностью аппроксими­руется нормальным распределением.

Это свойство используется для приближенного выражения квантилей распределения χ² (k) через квантили и_р нор­мального распределения N(0,1). Обычно используют следующие две формулы:

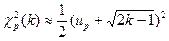и .

Первая формула, применяемая при к≥30 и р≥ 0,5,дает относительную погрешность в пределах 1%, а вторая формула применяется для вычисления квантилей малого порядка.

Пример 43. Вычислить квантили , , .

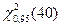Решение. По таблице приложений (П5) находим 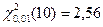. Для вычисления квантили 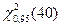воспользуем­ся первой формулой. Так как и_0,95 = 1,645 (см. таблицу приложе­ние П1), то .

По второй формуле, используя значение и_0,01 = и_0,99 = -2,326 получаем .

б) Распределением Стъюдента с k степенями свободы на­зывается распределение случайной величины Т(k), равной отно­шению двух независимых случайных величин U и , т. е.

,

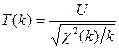где U имеет нормальное распределение N(0,1). Распределение Стьюдента с k степенями свободы будет также обозначаться Т(k). Распределение Стьюдента с k степенями свободы имеет плотность f_T(x) (рис. 13):

Рис. 13.

, -∞< x <+∞,

среднее М[Т(к)] = 0 и дисперсию , к > 2.

Плотность распределения Стьюдента симметрична относи­тельно оси ординат, тогда для квантилей t_p(k) имеет место соот­ношение t_p(k) = - t_1-p(k).

При больших k (k>30) для квантилей t_p(k) распределения Стьюдента выполнено приближенное равенство t_p(к) ≈ и_р. Более точная формула имеет вид .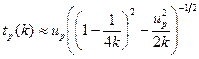

Пример 44. Найти квантили t_0,05(8) и t_0,90(40).

Решение. По таблице приложений (П6) находим t_0,95(8) = l,86; t_0,05(8) = -t_0,95(8) = -l,86. Квантиль t_0,90(40) опреде­лим, используя записанную выше формулу. Так как и_{0, 90} = 1,28 по таблице приложений (П1), то

Точное значение квантили t_0,90(40) по таблице приложений (П6) равно 1,303.

в) Распределением Фишера с k₁ и k₂ степенями свободы называется распределение случайной величины F(k₁,k₂), равной отношению двух независимых случайных величин 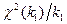и , т.е .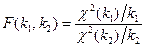

Распределение Фишера с k₁ и k₂ степенями свободы обо­значается так: F(k₁,k₂). Распределение Фишера с k₁ и k₂ степенями свободы имеет плотность f_F(x) (рис. 14):

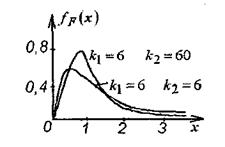
Рис. 14.

.

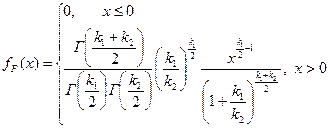среднее , .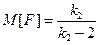

Квантили распределения Фишера порядка р и 1 - р связаны между собой так: .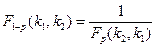

Между случайными величинами, имеющими нормальное распределение, распределения χ² Стьюдента и Фишера, имеют место соотношения: Т²(k) = F( 1 ,k), и .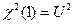

При k₁ > 1 и k₂ > 1 квантили распределения Фишера можно вычислить, используя приближенную формулу

.

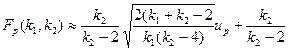Пример 45. Найти следующие квантили F_0,01(3,5), F_0,90(4,100) и F_0,05(60,120).

Решение. Используя известное соотношение и таблицу при­ложений (П7), получаем .

Далее находим .

Далее находим, используя значение u _0,05 =- u _0,95 =-1,645, .

По таблице приложений (П7) значение квантили F _0,05(60,120) равно .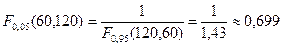

Дата добавления: 2014-11-20