Элементы теории корреляции

На практике часто приходится сталкиваться с зависимостью между различными признаками, например, между длиной тела рыбы и ее весом, между толщиной снегового покрова и объемом стока последующего половодья. Обычно эта зависимость более общего типа, чем функциональная - корреляционная или стохас­тическая вероятностная зависимость. При корреляционной зави­симости каждому значению одной случайной величины соответ­ствует ряд распределения другой случайной величины.

Корреляционный анализ наряду с выборочным методом представляет собой важнейшее прикладное направление математической статистики. Предметом его исследования является связь (зависимость) между различными варьирующими признаками (пе­ременными величинами), при которой каждому значению одной переменной соответствует не определенное значение другой (как это имеет место при функциональной зависимости), а ряд распре­деления с определенной групповой средней. При изучении этой важной темы следует уяснить сущность статистической и ее част­ного случая - корреляционной зависимости.

Конечная цель корреляционного анализа - получение урав­нений прямых регрессии, характеризующих форму зависимости, и вычисление коэффициента корреляции, определяющего тесноту (силу) связи, если она линейная.

Расчет производится в два основных этапа. На первом об­рабатывают табличные данные для нахождения величин , ,σ_х, σ_у и μ. При этом используется упрощенная схема вычисле­ния (т.е. переход от х_i и у_i к условным переменным), а далее применяются расчетные формулы.

Графическое изображение прямых регрессии (обе должны быть построены на одном чертеже) служит для контроля пра­вильности расчетов: они должны образовывать с осью ОХ либо только острые, либо только тупые углы в зависимости от знака μ, (или r), опытные точки с координатами ( , 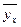) и (х_y,у) долж­ны располагаться по обе стороны соответствующих прямых рег­рессии; прямые регрессии должны пересекаться в центре распре­деления ( ; ).

Чертеж следует выполнять четко и аккуратно, удачно выби­рая масштабы по каждой оси (они могут быть разными) и начала отсчетов.

Все расчеты следует вести с разумной степенью точности (как правило, сохраняя два знака после запятой в окончательных данных). Для этого в промежуточных вычислениях достаточно сохранить три знака после запятой (правило «лишней» цифры).

Прежде чем проводить вычисления, нужно записать соот­ветствующие расчетные формулы.

Особенно внимательно отнеситесь к расчетам в таблицах, так как допущенная ошибка приведет к неустранимым погрешно­стям в окончательных результатах.

В конце решения надо кратко сформулировать окончатель­ные результаты и дать характеристику исследуемой корреляцион­ной зависимости (по величине, знаку коэффициента корреляции и оценке его достоверности).

Пример 61. Результаты измерения диаметров (х) и высот (у) 250 сосен записаны в таблицу.

x   y

Составить уравнения регрессии и найти коэффициент кор­реляции.

Уравнения регрессии имеют вид:

,

,

где и - средние значения величин х и у;

σ_х и σ_у - средние квадратические отклонения величин х и у;

r_в - выборочный коэффициент корреляции, вычисляемой по формуле: .

Для определения всех этих величин пользуемся методом произведений. Дополним данную таблицу несколькими строками и столбцами.

На основании метода произведений запишем, что

,

,

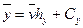где С_x и С_y - значения величин х и у, имеющих большую частоту;

u, v - средние значения условных вариант, вычисление по фор мулам:

; ; ; ,

где h_x и h_y -разность между соседними значениями X и Y.

Вычислим и :

,

.

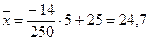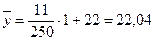Пользуясь методом произведений, находим средние квадратические отклонения величин х и у:

, .

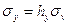Вычислим σ_u и σ_v по формулам средних квадратических отклонений:

,

,

.

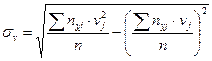Находим: , .

При переходе к условным вариантам и коэффициент корре­ляции имеет вид:

.

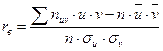Для вычисления величины 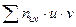применяется метод «че­тырех полей». Строка и столбец, на пересечении которых нахо­дится наибольшая частота (49), делят таблицу на четыре поля. В верхнем углу каждой заполненной клетки, расположенной в од­ном из четырех полей, записываем соответствующие произведе­ния uv, а затем подсчитываем сумму произведений 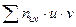. Оп­ределяем, сколько раз n_uv встречаются произведения uv.

Получаем:

Определим коэффициент корреляции

.

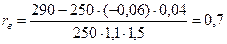Напишем уравнения регрессий

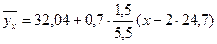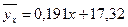или ,

или .

Имея уравнение регрессии, можно вычислить средние зна­чения одной величины при любом значении другой.

Дата добавления: 2014-11-20