
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Критерии значимости для проверки гипотез о средних нормально распределенной генеральной совокупности
|
|
|
|
Критерий Бартлетта для сравнения дисперсий нескольких совокупностей
Критерии значимости для проверки гипотез о дисперсиях нормально распределенной генеральной совокупности
| Проверяемая гипотеза Н0 | Предположение относительно т | Статистика Z критерия* | Распределение Z: f(z/H0) | Область принятия гипотезы Н0 для двустороннего критерия | Альтернативная гипотеза и область принятия гипотезы Н0 для правостороннего критерия | ||
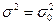
| т известно | 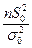
| 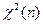
| 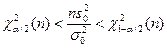
| 

| ||
т неизвестно,
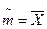
| 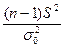
| 
| 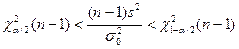
| 

| |||
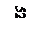 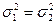
| т1 и т2 известны |  , ,
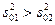
| 
| 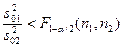
| 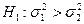

| ||
т1 и т2 неизвестны,
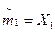 , ,
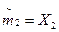
| 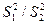 , ,

| 
| 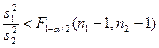
| 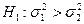
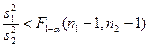
|
* Значение статистики z приведено при условии, что верна гипотеза Н0.
Таблица 7
| Н0 | Предположение относительно тi | Статистика Z критерия* | f(z/H0) | Область принятия гипотезы |
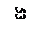 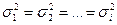
| тi неизвестны, i= 1, 2, …, l | 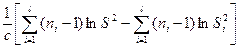 ,
где ,
где
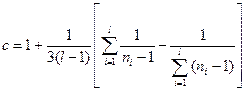 , ,
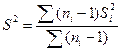 . .
| 
| 
|
* Значение статистики z приведено при условии, что верна гипотеза Н0.
Таблица 8
| Проверяемая гипотеза Н0 | Предположение относительно 
| Статистика Z критерия* | Распределение Z: f(z/H0) | Область принятия гипотезы Н0 для двустороннего критерия | Альтернативная гипотеза и область принятия гипотезы Н0 для правостороннего критерия |
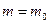
|  известна известна
| 
| 
| 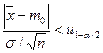
|  ; ; 
|
 неизвестна неизвестна
| 
| 
| 
|  ; ; 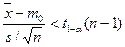
| |
|  и и  известны известны
| 
| 
| 
| 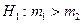 ; ; 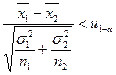
|
 и и  неизвестны, причем гипотеза Н0: неизвестны, причем гипотеза Н0: 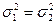 принимается, принимается,  ; ; 
| 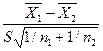 , где , где 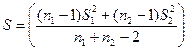
| 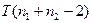
| 
| 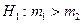 ; ; 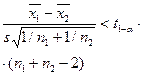
| |
 и и  неизвестны, причем гипотеза Н0: неизвестны, причем гипотеза Н0: 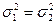 отклоняется, отклоняется, 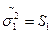 ; ; 
| 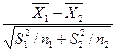
| 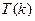 , где , где 
| 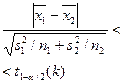
| 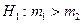 ; ; 
|
* Значение статистики z приведено при условии, что верна гипотеза Н0.
12.4. Проверка гипотез о параметре р биномиального распределения
При статистическом анализе данных, связанных с повторными независимыми испытаниями (схемой Бернулли), рассматривают два типа задач: сравнение вероятности «успеха» р в одном испытании с заданным значением р0 и сравнение вероятностей «успеха» в двух сериях испытаний.
В первом случае проверяется гипотеза Н0: р = р0. Пусть в п испытаниях по схеме Бернулли «успех» произошел х раз. В качестве статистики критерия выбирают относительную частоту h = x/n, nh > 5, n (1- h) > 5. При больших значениях n (n >50) и при выполнении условий nh > 5, n (1- h)>5 распределение случайной величины h в достаточной для практических расчетов точностью аппроксимируется нормальным распределением  . Отсюда следует, что если гипотеза Н0 верна, то статистика
. Отсюда следует, что если гипотеза Н0 верна, то статистика 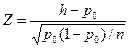 имеет распределение, близкое к нормальному распределению N (0,1). Критическая область критерия при уровне значимости α определяется неравенствами:
имеет распределение, близкое к нормальному распределению N (0,1). Критическая область критерия при уровне значимости α определяется неравенствами:
zB > u 1-α при альтернативной гипотезе 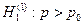 ,
,
zB < u α при альтернативной гипотезе  ,
,
|zB| > u 1-α/2 при альтернативной гипотезе  .
.
Для проверки гипотезы Н 0: р = р 0 также можно использовать доверительные интервалы для параметра р. При этом гипотеза Н 0 принимается на уровне значимости α, если соответствующий односторонний или двусторонний доверительный интервал накрывает значение р 0; иначе гипотеза Н 0 отклоняется.
Рассмотрим решение следующего типового примера.
Пример 54. Предполагается, что большая партия деталей содержит 15 % брака. Для проверки из партии случайным образом отобрано 100 деталей, среди которых оказалось 10 бракованных.
Считая, что число бракованных деталей в партии имеет биномиальное распределение, и используя двусторонний критерий при α = 0,05, проверить предположение о том, что в партии содержится 15 % бракованных деталей.
Решение. Проверяется гипотеза Н 0: р = 0,15 при альтернативной гипотезе Н 1: р ≠ 0,15. Значение 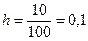 . Так как п > 50, nh = 10 и n (1 - h) = 9, то для проверки гипотезы Н 0 можно использовать известную статистику. Выборочное значение этой статистики:
. Так как п > 50, nh = 10 и n (1 - h) = 9, то для проверки гипотезы Н 0 можно использовать известную статистику. Выборочное значение этой статистики:
 .
.
По таблице приложений (П1) находим u 0,975 = 1,96. Значение |zB| лежит в области принятия гипотезы Н 0, следовательно, предположение о том, что в партии содержится 15 % брака, согласуется с результатами наблюдений. Этот же результат получим, используя двусторонний доверительный интервал (0,041;0,159) для р при доверительной вероятности 0,95. Так как этот доверительный интервал накрывает значение р = 0,15, гипотеза Н 0 принимается.
13.5. Проверка гипотез о коэффициенте корреляции р.
Пусть r - выборочный коэффициент корреляции, вычисленный по выборке объема п из генеральной совокупности, имеющей двумерное нормальное распределение.
Для проверки гипотезы Н0:ρ = ρ0, где ρ0 - заданное значение, используют статистику:
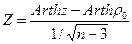 .
.
Если гипотеза Н 0 верна, то эта статистика имеет распределение, близкое к нормальному N(0,1).
Критическая область критерия при уровне значимости α определяется неравенствами:
zB > u 1-α при альтернативной гипотезе 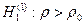 ,
,
zB < u α при альтернативной гипотезе  ,
,
|zB| > u 1-α/2 при альтернативной гипотезе  .
.
В случае, когда нужно определить значимость выборочного значения коэффициента корреляции r, т.е. проверить гипотезу Н 0: ρ = 0, можно использовать другой критерий, статистикой которого является r. На уровне значимости α критическая область этого критерия определяется неравенствами

при альтернативной гипотезе 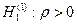 ;
;

при альтернативной гипотезе 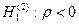 ;
;

при альтернативной гипотезе 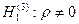 .
.
Пример 55. Из генеральной совокупности, имеющей двумерное нормальное распределение, получена выборка объема n = 67. Выборочный коэффициент корреляции оказался равным r =-0,159. Можно ли считать, что наблюдаемые переменные отрицательно коррелированны, если уровень значимости α = 0,05?
Решение. Проверим гипотезу Н 0: ρ = 0 при альтернативной гипотезе  . Вычислим выборочное значение статистики критерия. Значение Arth r находим по таблице приложений (П8).
. Вычислим выборочное значение статистики критерия. Значение Arth r находим по таблице приложений (П8).
Имеем 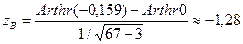 .
.
Используя таблицы приложений, находим, что u 0,05 = -1,645. Отсюда делаем вывод о том, что выборочное значение статистики критерия принадлежит области принятия гипотезы Н 0, следовательно, наблюдаемые переменные некоррелированы.
Такой же результат получим, воспользовавшись критерием, статистикой которого является r. Найдем границу критической области при альтернативной гипотезе  . Определим квантили t 0,05 (65)= t 0,95 (65)≈-1,67 (таблица приложений (П6)). Вычислим границу критической области:
. Определим квантили t 0,05 (65)= t 0,95 (65)≈-1,67 (таблица приложений (П6)). Вычислим границу критической области:
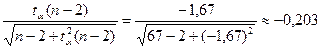
Выборочное значение r = -0,159 статистики принадлежит области принятия гипотезы Н 0, то гипотеза Н 0 принимается; отсюда следует, что наблюдаемые переменные некоррелированы.
Пусть r1 и r 2 - выборочные коэффициенты корреляции, вычисленные по выборкам объема п1 и п2 из генеральных совокупностей, имеющих двумерное нормальное распределение. Для проверки гипотезы  используют статистику:
используют статистику:
 .
.
При условии, что гипотеза Н 0 верна, рассматриваемая статистика имеет распределение, близкое к нормальному распределению N(0,1). Критическая область критерия при уровне значимости α определяется неравенствами:
zB > u 1-α при альтернативной гипотезе 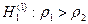 ,
,
zB < u α при альтернативной гипотезе 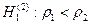 ,
,
|zB| > u 1-α/2 при альтернативной гипотезе 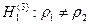 .
.
Пример 56. Сравнить коэффициенты корреляции двух нормально распределенных генеральных совокупностей по следующим выборочным данным: r1 = 0,77, п1 = 28, r 2 = 0,604, п2 = 33. Считать α =0,10.
Решение. Имеем 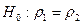 ;
; 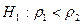 . Вычислим выборочное значение данной статистики критерия:
. Вычислим выборочное значение данной статистики критерия:
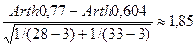 .
.
Так как и0,95 ≈1,645, то выборочное значение статистики критерия принадлежит критической области; коэффициенты корреляций генеральных совокупностей следует считать различными.
12.6. Определение наилучшей критической области для проверки простых гипотез.
Следует заметить, что на множестве значений статистики критерия можно выбрать сколько угодно критических областей VK для заданного уровня значимости α, однако соответствующие им критерии будут иметь различные вероятности ошибок второго рода.
Наилучшей критической областью (НКО) называют критическую область, которая при заданном уровне значимости α обеспечивает минимальную вероятность ошибки второго рода. Критерий, использующий НКО, имеет максимальную мощность.
При проверке простой гипотезы Н 0 против простой альтернативы Н 1 НКО определяется леммой Неймана - Пирсона: НКО критерия заданного уровня значимости α состоит из точек, выборочного пространства (выборок объема п), для которых удовлетворяется неравенство 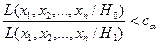 , где сα - константа, зависящая от заданного уровня значимости,
, где сα - константа, зависящая от заданного уровня значимости, 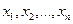 - элементы выборки, а
- элементы выборки, а 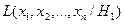 -функция правдоподобия, вычисленная при условии, что верна гипотеза Нi,i = 0,1.
-функция правдоподобия, вычисленная при условии, что верна гипотеза Нi,i = 0,1.
Для рассмотренных выше критериев значимости, НКО размещаются на «хвостах» распределений статистик критериев.
Пример 57. Пусть случайная величинах имеет нормальное распределение N(m, σ) с известной дисперсией σ2.
а) Найти НКО для проверки гипотезы Н0:т = т0 против простой альтернативной гипотезы Н 1 :m = m1, где т1 > т0.
б) Найти функцию мощности критерия и вычислить ее значение при значениях т1 = 1 и т1 = 5, если т0 = 0, объем выборки п = 25, дисперсия генеральной совокупности σ2 = 25. Принять уровень значимости α = 0,05.
Решение. а) Запишем отношение функций правдоподобия:
 ,
,
где 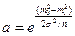 ,
,  . По лемме Неймана - Пирсона НКО содержит только те точки выборочного пространства, для которых удовлетворяется неравенство
. По лемме Неймана - Пирсона НКО содержит только те точки выборочного пространства, для которых удовлетворяется неравенство 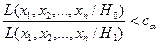 :
:
 ,
,
причем по условию задачи т1 - т0 > 0. Так как отношение правдоподобия является убывающей функцией аргумента  , условие леммы удовлетворяется при
, условие леммы удовлетворяется при  , где граница критической области хк находится по заданному уровню значимости α из соотношения
, где граница критической области хк находится по заданному уровню значимости α из соотношения  .
.
При условии, что справедлива гипотеза Н0, 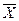 имеет нормальное распределение
имеет нормальное распределение  , следовательно,
, следовательно,
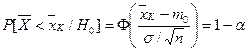 .
.
Отсюда следует, что:
 .
.
Таким образом, граница хк критической области равна 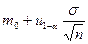 , а НКО V K имеет вид
, а НКО V K имеет вид  .
.
б) Найдем функцию мощности полученного критерия:
 .
.
При значениях т1 = 1, т0 = 0, α = 0,05, n = 25, σ2 = 25 мощность критерия
 .
.
Если т1 = 5, то мощность критерия
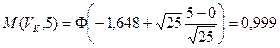 .
.
12.7. Критерий χ2 и его применение
а) Проверка гипотезы о виде распределения генеральной совокупности.
Пусть х1,х2,...,хn - выборка наблюдений случайной величины X. Проверяется гипотеза Н 0, утверждающая, что χ2 имеет функцию распределения Fx (x).
Проверка гипотезы Н 0 при помощи критерия χ2 осуществляется по следующей схеме: по выборке наблюдений находят оценки неизвестных параметров предполагаемого закона распределения случайной величины X. Далее, область возможных значений случайной величины X разбивается на r множеств Δ1, Δ2,…, Δn, например, r интервалов в случае, когда Х - непрерывная случайная величина, или r групп, состоящих из отдельных значений, для дискретной случайной величины X.
Пусть n k - число элементов выборки, принадлежащих множеству Δk, k = 1,2,..., r. Тогда  . Используя предполагаемый закон распределения случайной величины X, находят вероятности рk того, что значение X принадлежит множеству Δk, т.е.
. Используя предполагаемый закон распределения случайной величины X, находят вероятности рk того, что значение X принадлежит множеству Δk, т.е.
рk = Р [ Х Î Δk], k = 1,2,..., r. Очевидно, что 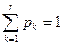 . Полученные результаты можно представить в виде следующей таблицы:
. Полученные результаты можно представить в виде следующей таблицы:
| Число наблюдений | Всего | ||||
| Δ1 | Δ2 | … | Δr | ||
| Наблюдаемое | n 1 | n 2 | … | n r | п |
| Ожидаемое | np 1 | np 2 | … | np r | п |
Выборочное значение статистики критерия χ2 вычисляется по формуле 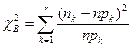 .
.
Гипотеза Н0 согласуется с результатами наблюдений на уровне значимости α, если
 ,
,
где 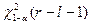 квантиль порядка 1- α распределения χ2 с r-l -1 степенями свободы, а l - число неизвестных параметров распределения, оцениваемых по выборке; если же
квантиль порядка 1- α распределения χ2 с r-l -1 степенями свободы, а l - число неизвестных параметров распределения, оцениваемых по выборке; если же 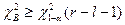 , то гипотеза Н0 отклоняется.
, то гипотеза Н0 отклоняется.
Замечание. Критерий χ2 использует тот факт, что случайная величина  , k = 1,2,..., r, имеет распределение, близкое к нормальному N (0,1).Чтобы это утверждение было достаточно точным, необходимо, чтобы для всех интервалов выполнялось условие прк ≥ 5. Если в некоторых интервалах это условие не выполняется, то их следует объединить с соседними.
, k = 1,2,..., r, имеет распределение, близкое к нормальному N (0,1).Чтобы это утверждение было достаточно точным, необходимо, чтобы для всех интервалов выполнялось условие прк ≥ 5. Если в некоторых интервалах это условие не выполняется, то их следует объединить с соседними.
Пример 58. В первых - двух столбцах таблицы 9 приведены данные об отказах аппаратуры за 10000 часов работы. Общее число обследованных экземпляров аппаратуры n =757, при этом наблюдался отказ:
0·427+ 1·235+ 2·72 + 3·21+ 4·1+ 5·1 = 451
Таблица 9
| Число отказов, k | Количество случаев, в которых наблюдалось k отказов, пk | 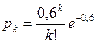
| Ожидаемое число случаев с k отказами, прk |
| 0,54881 | |||
| 0,32929 | |||
| 0,09879 | |||
| 0,01976 | |||
| 0,00296 | |||
| 0,00036 | |||
| ≥6 | 0,00004 | ||
| Сумма | - | - |
Проверить гипотезу о том, что число отказов имеет распределение Пуассона:
 , k =0, 1, …, при α= 0,01.
, k =0, 1, …, при α= 0,01.
Решение. Оценка параметра λ равна среднему числу отказов: 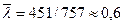 . По таблице приложений (П3) с λ = 0,6 находим вероятности рk и ожидаемое число случаев с k отказами (третий и четвертый столбцы таблицы 10).
. По таблице приложений (П3) с λ = 0,6 находим вероятности рk и ожидаемое число случаев с k отказами (третий и четвертый столбцы таблицы 10).
Для k = 4,5 и 6 значения прk < 5, поэтому объединяем эти строки со строкой для k = 3. Итак, получаем значения, приведенные в таблице 9.
Таблица 10
| k | пk | прk | 
|
| 427 | 0,291 | ||
| 0,787 | |||
| 0,120 | |||
| ≥3 | 2,118 | ||
| - | - | - | 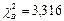
|
Так как по выборке оценивался один параметр λ, то l = 1, число степеней свободы равно 4-1-1 = 2. По таблице приложений (П5) находим χ2 0,99(2) = 9,21, гипотеза о распределении числа отказов по закону Пуассона принимается.
Пример 59. Проверить гипотезу о нормальном распределении выборки из примера 51. Принять α = 0,1.
Решение. Объем выборки п = 55. Для проверки гипотезы о нормальном распределении нужно найти оценки математического ожидания и дисперсии. Имеем
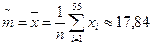 ,
,
 .
.
Воспользуемся результатами группировки выборки примера 50, расширив первый и последний интервалы. Результаты группировки приведены во втором и третьем столбцах таблицы 11.
Таблица 11
| Номер интервала k | Границы интервала Δ k | Наблюдаемая частота nk | Вероятность попадания в интервал Δ k, pk | Ожидаемая частота, npk | npk | nk - npk | 
|
| - ∞ - | |||||||
| 0 0228 | 
| 5,274 | |||||
| 12-14 | 0,0731 | 0,725 | 0,010 | ||||
| 14-16 | 0,1686 | 9,273 | 9,273 | -1,273 | 0,175 | ||
| 16-18 | 0,2576 | 14,168 | 14,168 | -2,168 | 0,332 | ||
| 18-20 | 0,2484 | 13,662 | 13,662 | -2,338 | 0,400 | ||
| 20-22 | 0,1519 | 
| 12,633 | ||||
| 22- | 0,0778 | 0,366 | 0,011 | ||||
| + ∞ | |||||||
| Сумма | 1,0001 | - | 0,928 |
В четвертом столбце таблицы 11 приведены вероятности рk, вычисляемые по формуле:
 ,
,
где ак и bк - соответственно нижняя и верхняя границы интервалов, а значения функции Ф(х) берутся из таблицы приложений (П1). В пятом столбце приводятся ожидаемые частоты прk, а в шестом - значения прk после объединения первых двух и последних двух интервалов.
Так как после объединения осталось r = 5 интервалов, а по выборке определены оценки двух параметров, т.е. l = 2, то число степеней свободы равно 5-2-1 = 2.
По таблице приложений (П5) находим χ2 0,90(2) = 4,61. Выборочное значение статистики критерия равно χ2 B = 0,928, следовательно, гипотеза о нормальном распределении выборки принимается.
б) Проверка гипотезы о независимости двух случайных величин.
Пусть проведено п экспериментов, результаты которых являются значениями дискретных случайных величин X и Y, которые принимают соответственно значения x1,x2,...,xk и у1,у2,...,уl.
Обозначим пij число экспериментов, в которых X = хi и Y =yj, i = 1,2,..., k; j = 1,2,..., l. Если Х и Y- непрерывные случайные величины, то область значений каждой из них разбивается на конечное число интервалов. В этом случае пij - число экспериментов, в которых случайная величина X попала в i -й интервал, а случайная величина Y -в j -й интервал. Результаты п экспериментов можно представить в виде таблицы сопряженности признаков размера k x l (таблица 12).
Проверяется гипотеза Н0, утверждающая, что случайные величины X и Y независимы. Если гипотеза Н0 верна, то по определению:
 .
.
Пусть  и
и 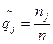 -оценки вероятностей рi и qj.
-оценки вероятностей рi и qj.
Если гипотеза Н0 верна, то ожидаемое число экспериментов 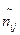 , в которых случайная величина X попала в i- й интервал, а случайная величина Y - в j -й интервал, равно
, в которых случайная величина X попала в i- й интервал, а случайная величина Y - в j -й интервал, равно
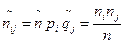 .
.
Для проверки гипотезы Н0 по критерию χ2 используют следующую статистику: 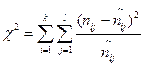 .
.
При условии, что гипотеза Н0 верна, а все ожидаемые частоты 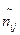 ≥ 4, i = 1,2,..., k; j = 1,2,..., l, указанная статистика имеет распределение χ2 с (k _1)(l -1) степенями свободы.
≥ 4, i = 1,2,..., k; j = 1,2,..., l, указанная статистика имеет распределение χ2 с (k _1)(l -1) степенями свободы.
Гипотеза Н0 о независимости случайных величин X и Y принимается на уровне значимости α, если выборочное значение этой статистики меньше квантили χ2 1-α((k -1)(l -1)), т.е. если χ2 В< χ2 1-α((k -1)(l -1)).
Если χ2 В≥ χ2 1-α((k -1)(l -1)) гипотеза Н0 отклоняется. Для вычисления выборочного значения статистики критерия удобно использовать формулу
 .
.
Замечания. 1. Если ожидаемые частоты nij для некоторых клеток таблицы 12 не удовлетворяют условию 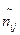 ≥ 4, то соответствующие строки и столбцы должны быть объединены с соседними строками и столбцами.
≥ 4, то соответствующие строки и столбцы должны быть объединены с соседними строками и столбцами.
Таблица 12
| Y X | y 1 | y 2 | … | yl | 
|
| x 1 | n 11 | n 12 | … | n 1 l | n 1 |
| x 2 | n 21 | n 22 | … | n 2 l | n 2 |
| … | … | … | … | … | … |
| xk | nk 1 | nk 2 | … | nkl | nk |
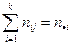
| n 1 | n 2 | … | nl | n••=n |
2. Если (k -1)(l -1)≥8 и n ≥40, то минимальное допустимое значение ожидаемых частот может быть равным единице.
Случайные величины X и Y можно рассматривать как два признака, по которым классифицируется выборка объема п; независимость X и Y соответствует независимости этих признаков.
Во многих случаях требуется проверить гипотезу об однородности нескольких выборок или, другими словами, гипотезу о том, что эти выборки получены из одной генеральной совокупности. Если проверяется однородность k различных выборок с объемами п1,п2,...,пk и эти выборки могут быть записаны в виде таблицы сопряженности признаков размера k х l (см. табл. 12), то для проверки используется тот же критерий, что и для проверки независимости двух признаков.
Пример 60. Комплектующие изделия одного наименования поступают с трех предприятий А, В и С. Результаты проверки изделий следующие:
| Результаты проверки | Поставщики | Всего | ||
| А | В | С | ||
| Годные | ||||
| Негодные | ||||
| Всего |
Можно ли считать, что качество изделий не зависит от поставщика? Принять α = 0,10.
Решение. Проверим гипотезу о независимости двух признаков: качества изделия и места его изготовления. Находим
 ;
;
число степеней свободы (2 —1)(3 — 4) = 2. Так как по таблице приложений (П5) χ2 0,90(2) = 4,605, то это означает, что качество изделий не зависит от поставщика.
Заметим, что утверждение о том, что качество изделий не зависит от поставщика, можно трактовать как проверку гипотезы об однородности трех выборок изделий объемом 30, 40 и 60, полученных соответственно от поставщиков А, В и С.
12.8. Методика вычисления теоретических частот нормального распределения
Сущность критерия Пирсона состоит в сравнении эмпирических и теоретических частот. Эмпирические частоты находят из опыта. Как найти теоретические частоты, если предполагается, что генеральная совокупность распределена нормально?
Укажем один из способов решения этой задачи.
1. Весь интервал наблюдаемых значений X делят на s частичных интервалов (хi; хi +1) одинаковой длины. Находят середины частичных интервалов  ; в качестве частоты ni варианты
; в качестве частоты ni варианты  принимают число вариант, которые попали в i -й интервал. В итоге получают последовательность равноотстоящих вариант и соответствующих им частот:
принимают число вариант, которые попали в i -й интервал. В итоге получают последовательность равноотстоящих вариант и соответствующих им частот:
 , п1,п2,...,пs,
, п1,п2,...,пs,
причем  .
.
2. Вычисляют, например, методом произведений или сумм, выборочную среднюю 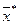 и выборочное среднее квадратическое отклонение σ*.
и выборочное среднее квадратическое отклонение σ*.
3. Нормируют случайную величину X, т.е. переходят к величине: 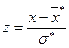 , и вычисляют концы интервалов (zi; zi +1):
, и вычисляют концы интервалов (zi; zi +1):
 ,
,  ,
,
причем наименьшее значение, т.е. z 1 полагают равным -∞, а наибольшее, т.е. zs полагают равным ∞.
4. Вычисляют теоретические вероятности pi попадания х в интервалы (хi; хi +1)по равенству (Ф(z) функция Лапласа)

и наконец находят искомые теоретические частоты ni’ = npi.
12.9. Модель применения критериев
Статистические критерии проверки гипотез разнообразны, но у них единая логическая схема построения, представленная на рисунке 17.
 |
Рис. 17
13. Рекомендации представления результатов статистической обработки для различных критериев и методов анализа «Метода проверки гипотез или статистических критериев»
| п/п | Метод проверки гипотез или статистический критерий | Содержание рекомендуемого описания |
| Проверка гипотез о законе распределения | Наименование закона распределения, на соответствие которому производится проверка. Название статистического критерия, с помощью которого производится проверка гипотез, полученная величина данного критерия и отвечающее ему значение достигнутого уровня значимости. | |
| Проверка равенства двух законов распределения вероятностей | Сформулировать причины проверки данной гипотезы, указать статистический критерий для проверки его значения и достигнутый уровень значимости. Сделать вывод о том, какая из гипотез принимается, и какой из этого следует вывод применительно к целям исследования. | |
| Проверка нормальности распределения вероятности | Сформулировать причины проверки данной гипотезы, указать статистический критерий для проверки его значения и достигнутый уровень значимости. Сделать вывод о том, какая из гипотез принимается и какой из этого следует вывод применительно к целям исследования. Желательно привести график распределения на «вероятностной бумаге». | |
| Критерий Колмогорова-Смирнова | Указать, какой именно из семейства критериев использовался в конкретном случае и цель его применения (сформулировать проверяемые гипотезы). Привести значение критерия и достигнутый уровень значимости. По результатам проверки сформулировать вывод относительно выдвигаемых гипотез. | |
| Уровень значимости «р=...» | Обязательное указание, к какому конкретному статистическому критерию относится данное значение уровня значимости. Не употреблять выражения вида «р <...» или «р >...». | |
| Оценка дескриптивных статистик | Объем выборки (подгрупп), среднее, стандартное отклонение, ошибка среднего. При сравнении вариабельности двух и более признаков - коэффициент вариации. Обязательно сообщить, использовались ли методы оценки аномальных наблюдений (выбросов) и если - да, то какие. Сообщить, применялись ли методы робастного оценивания (Пуанкаре, Винзора, Хубера и т.д.) | |
| Проверка гипотез о равенстве дисперсий с помощью F — критерия Фишера | Предварительно провести проверку имеющегося ограничения на использование F - критерия Фишера. Вычислить значение критерия и достигнутого уровня значимости. Сделать вывод о том, какая из конкурирующих гипотез принимается, дать интерпретацию этого результата. | |
| Проверка гипотез о равенстве дисперсий с помощью критериев Кохрэта, Бартлетта и др. | Сформулировать проверяемую гипотезу о равенстве нескольких дисперсий и указать используемый для этого статистический критерий. Вычислить значение критерия и достигнутого уровня значимости. Сделать вывод о том, какая из конкурирующих гипотез принимается, дать интерпретацию этого результата. При использовании критерия Бартлетта обязательно привести результаты проверки нормальности во всех сравниваемых группах. | |
| F — критерий Фишера | Сообщить, для проверки каких именно статистических гипотез использовался данный критерий, степени свободы для него и достигнутый уровень значимости | |
| Сравнение двух выборок с помощью критерия | Дать описание природы количественного и группирующего признаков. Сообщить объемы наблюдений в сравниваемых группах. Сформировать гипотезу, которая проверяется с помощью данного критерия. Привести вычисленное значение z — критерия и величину достигнутого уровня значимости. Результат проверки гипотезы интерпретировать. |
|
|
|
|
|
Дата добавления: 2014-11-20; Просмотров: 1366; Нарушение авторских прав?; Мы поможем в написании вашей работы!